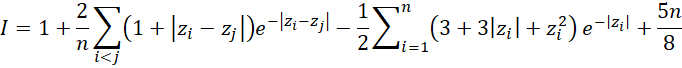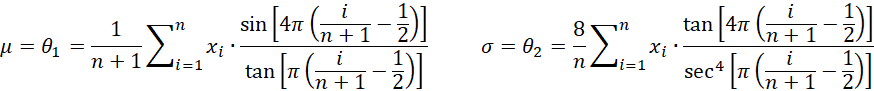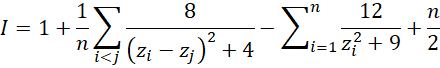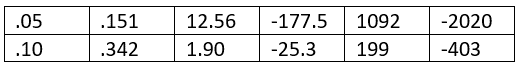We now extend the goodness-of-fit test based on the characteristic function to Laplace and Cauchy distributions.
Laplace Distribution
We now show how to test whether the data set X = {x1, …, xn} follows a Laplace distribution with pdf
Now we use the following estimates (these are the MLE estimates when n is odd)
The test statistic and critical values for this test are
Example
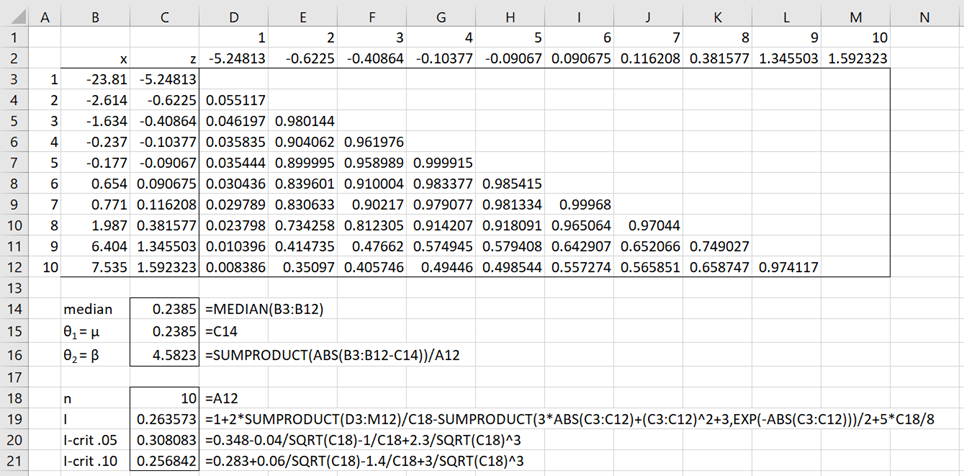
Example 1: Decide whether the data in B3:B12 of Figure 1 fits a Laplace distribution.
This example comes from the referenced textbook. Figure 1 describes the analysis. Note that cell C3 contains the formula =(B3-C15)/C16 and cell D3 contains the formula =IF(D$1<$A3,(ABS($C3-D$2)+1)*EXP(-ABS($C3-D$2)),””). The other formulas in C3:M12 are filled in as explained for Example 1 of Goodness-of-Fit Test based on the Characteristic Function.
Figure 1 – GoF for Laplace distribution
We see from Figure 1 that I = .263573 > .256842 = I.10, and so we have a significant result at the .10 level. But also I = .263573 < .308083 = I.05, which is not significant at the .05 level. In fact, the data comes from a Cauchy distribution.
Note that we obtain the same result using the formula =ICF_GOF(B3:B12,”laplace”,TRUE). See Goodness-of-Fit Test based on the Characteristic Function for a description of the ICF_GOF function and its arguments.
Cauchy Distribution
We now show how to test whether the data set X = {x1, …, xn} follows a Laplace distribution with pdf
We can estimate the parameters by
This is the approach used by CAUCHY_FITX (see Fitting a Cauchy Distribution) to estimate the parameters, except that there the first n+1 in the formula used to estimate μ is replaced by n.
Here it is important that values of X must be used in (ascending or descending) order.
The test statistic is given by
For even values of n starting with n = 16 for alpha .05, and n = 14 for alpha = .10, the critical values are:
Example
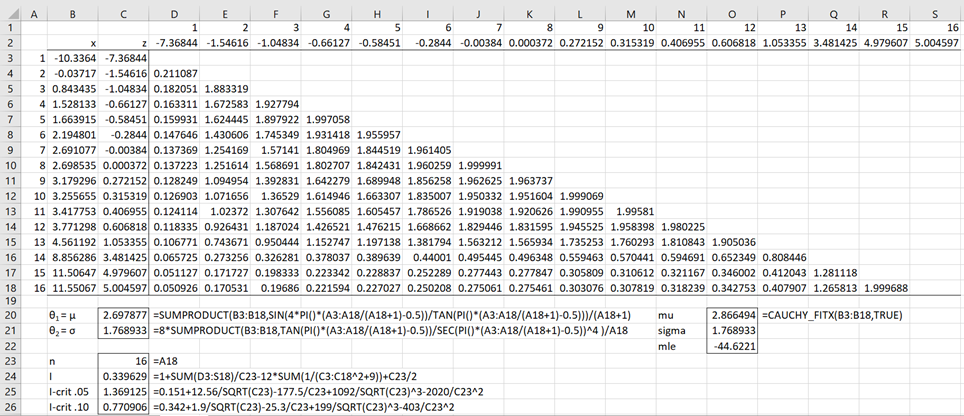
Example 2: Decide whether the data in B3:B18 of Figure 8 fits a Cauchy distribution.
Figure 2 describes the analysis. Note that cell C3 contains the formula =(B3-C20)/C21 and cell D3 contains the formula =IF(D$1<$A3,8/(($C3-D$2)^2+4),””). The other formulas in C3:S12 are filled in as explained for Example 1 of Goodness-of-Fit Test based on the Characteristic Function.
Figure 2 – GoF for a Cauchy distribution
We see from Figure 2 that I = .339629 < .770906 = I.10, and so we can’t reject the null hypothesis that the data comes from a Cauchy distribution.
This is not surprising since the data was constructed by inserting the formula =T3_INV(RAND(),1,2,1) in cell B3, highlighting B3:B18, and pressing Ctrl-D.
Note that we obtain the same result using the formula =ICF_GOF(B3:B18,”cauchy”,TRUE,-3). See Goodness-of-Fit Test based on the Characteristic Function for a description of the ICF_GOF function and its arguments.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Epps, T. W. (2014) Probability and statistical theory for applied researchers
https://books.google.co.uk/books?id=NCs8DQAAQBAJ&pg=PR4&lpg=PR4&dq=Epps,+T.+W.+Probability+and+statistical+theory+for+applied+researchers&source=bl&ots=GxU40vCNHu&sig=ACfU3U0vgZZndBfjMMmqYPQuCXAJf2jrow&hl=en&sa=X&ved=2ahUKEwiw5_3R-4KCAxVCgFwKHa2fA384FBDoAXoECAQQAw#v=onepage&q=Epps%2C%20T.%20W.%20Probability%20and%20statistical%20theory%20for%20applied%20researchers&f=false