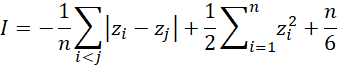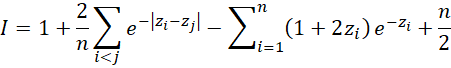GoF ICF Uniform & Exponential

We now extend the goodness-of-fit test based on the characteristic function to uniform and exponential distributions.

Uniform Distribution

For data X = {x₁, …, x_n} from a (continuous) uniform distribution on (a, b) with pdf

we use the estimates

a = min  X         b = max X

Now define

Thus

Define

We use the test statistic

The critical values I_α of this statistic for 10 ≤ n ≤ 400 are

Henceforth, we will abbreviate these critical values as

If If I ≥ I_α, then we reject the null hypothesis that the data comes from a uniform distribution.

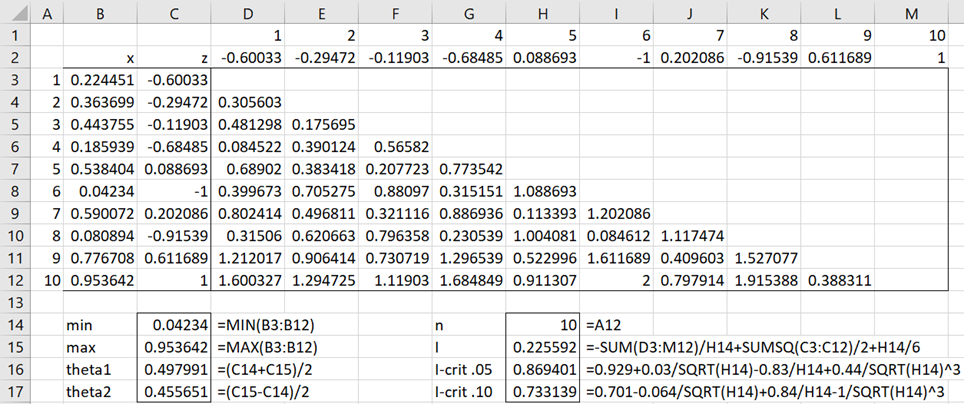
Example 1: Determine whether the data in column B of Figure 1 are uniformly distributed.

The analysis is also shown in Figure 1. Note that cell C3 contains the formula =(B3-C16)/C17 and cell D3 contains the formula =IF(D$1<$A3,ABS($C3-D$2),””). The other formulas in C3:M12 are filled in as explained in Example 1 of Goodness-of-Fit Test based on the Characteristic Function.

Figure 1 – GoF for uniform distribution

We see from Figure 5 that I = .225592 < .733139 = I_.10, and so we can’t reject the null hypothesis that the data is uniformly distributed.

We get the same results as shown in range G14:H17 via the array formula =ICF_GOF(B3:B12,”uniform”,TRUE). See Goodness-of-Fit Test based on the Characteristic Function for a description of the ICF_GOF function and its arguments.

Note that if we test the 10 data elements in B2:B11 of Figure 1 via the formula =ICF_GOF(B2:B11,”uniform”,TRUE), we obtain I-stat = 2.963459 > .869401 = I_.05. This is a significant result, providing evidence that the data is not uniformly distributed.

Exponential Distribution

For data X = {x₁, …, x_n} from an exponential distribution with pdf

We use the following MLE parameter estimates

The test statistic for this test is

The critical values when μ is unknown are

When μ is known then use the above table assuming n = 0 (i.e. I_.05 = .785 and I_.10 = .635).

Example

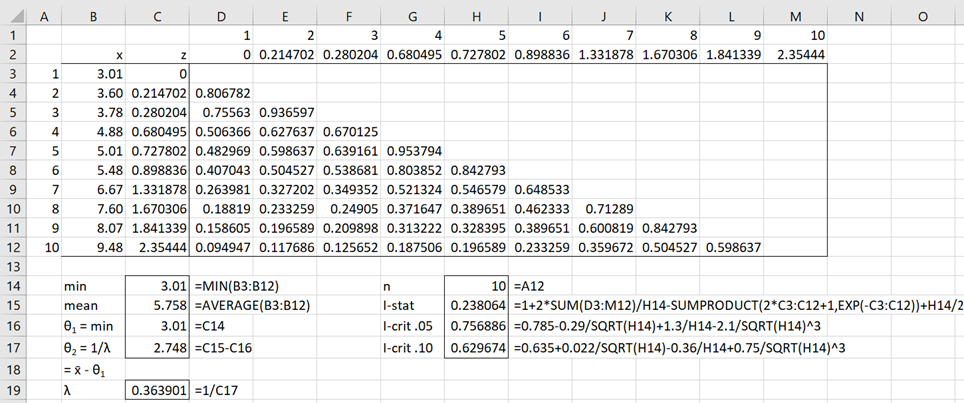
Example 2: Decide whether the data in B3:B12 of Figure 2 fits an exponential distribution.

This example comes from the referenced textbook. Figure 2 describes the analysis. Note that cell C3 contains the formula =(B3-C16)/C17 and cell D3 contains the formula =IF(D$1<$A3,EXP(-ABS($C3-D$2)),””). The other formulas in C3:M12 are filled in as explained in Example 1.

Figure 2 – GoF for Exponential distribution

We see from Figure 2 that I = .238064 < .629674 = I_.10, and so we can’t reject the null hypothesis that the data is uniformly distributed with pdf

f(x) = .363901e^{–.363901(x–3.01)}

We get the same results as shown in range G14:H17 via the array formula =ICF_GOF(B3:B12,”expon”,TRUE).

If instead, we know that μ = θ₁ = 0, then using the worksheet formula =ICF_GOF(B3:B12,”expon”,TRUE,,0) we see that I = 1.189405 > 785  = I_.05, and so p-value < .05, which is a significant result. Here we estimate λ = 1/5.758 = .173671. Thus, we conclude that the data doesn’t follow an exponential distribution, estimated by

f(x) = .173671e^–.173671x

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Epps, T. W. (2014) Probability and statistical theory for applied researchers
https://books.google.co.uk/books?id=NCs8DQAAQBAJ&pg=PR4&lpg=PR4&dq=Epps,+T.+W.+Probability+and+statistical+theory+for+applied+researchers&source=bl&ots=GxU40vCNHu&sig=ACfU3U0vgZZndBfjMMmqYPQuCXAJf2jrow&hl=en&sa=X&ved=2ahUKEwiw5_3R-4KCAxVCgFwKHa2fA384FBDoAXoECAQQAw#v=onepage&q=Epps%2C%20T.%20W.%20Probability%20and%20statistical%20theory%20for%20applied%20researchers&f=false