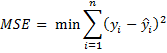In the usual (multiple) linear regression model, we seek regression coefficients that minimize the sum of the squares of the residuals, i.e.
Thus, the squaring of the residuals gives added weight in MSE to large residuals, i.e. those values of i for which ŷi is far from yi as compared to those values for which ŷi is close to yi. In particular, this gives greater weight to outliers, which may be undesirable.
The Least Absolute Deviation model instead minimizes the absolute value of the residuals, i.e.
This provides a more robust solution when outliers are present, but it does have some undesirable properties, most notably that there are some situations where there is no unique solution, and in fact an infinite number of different regression lines are possible.
When a unique solution does exist, then the LAD model has the desirable property that if there is one independent variable, then the regression line will pass through at least two of the data points; in fact, if there are k independent variables, then the residual of at least k + 1 of the data elements will be zero.
The ordinary least squares (OLS) method does not work for LAD regression. We show the following two methods that can be used instead to find the appropriate coefficients (at least when there is a unique solution).
In addition, we describe how to use bootstrapping to calculate the standard errors of the LAD regression coefficients and how to use the Real Statistics LAD Regression data analysis tool.
- Using Bootstrapping to find standard errors of LAD regression coefficients
- Real Statistics LAD Regression data analysis tool
References
Wikipedia (2016) Least absolute deviations
https://en.wikipedia.org/wiki/Least_absolute_deviations
Wikipedia (2016) Iteratively reweighted least squares
https://en.wikipedia.org/wiki/Iteratively_reweighted_least_squares
Thanoon, F. H. (2015) Robust regression by least absolute deviations method
http://article.sapub.org/10.5923.j.statistics.20150503.02.html