Example
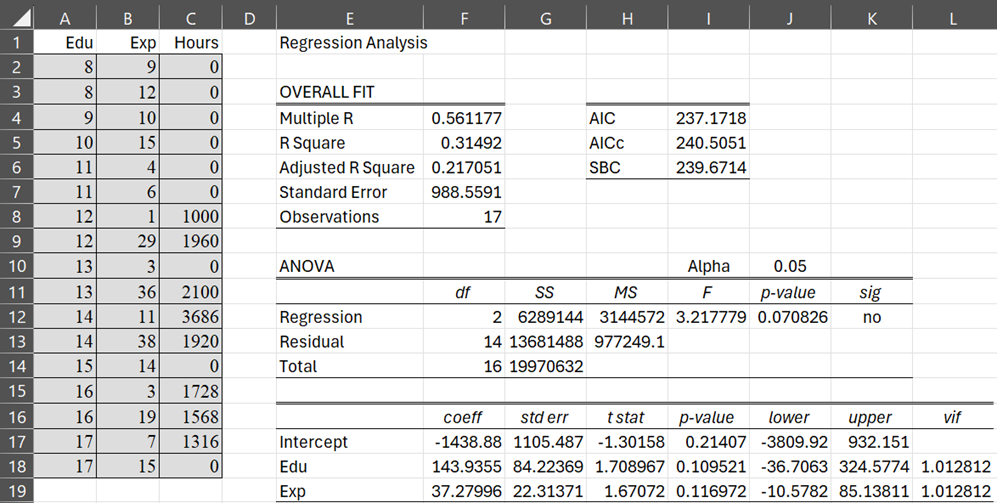
Example 1: In this example, we use a Tobit regression model to predict the number of hours a wife works outside the household (Hours) in a given year based on a small subset of the Mroz (1987) data set (as shown on the left side of Figure 1). The original data set contains data for 753 women and quite a few variables that might be useful in making the prediction (number of children, etc.). We will build our small model using only 17 of the rows of data and only the woman’s years of education (Edu) and years of work experience outside the home (Exp).
As you can see, 9 of the 17 data rows has the woman working zero hours, which means that the woman was not employed. The usual linear regression model is shown on the right side of Figure 1, although it is better to use a Tobit model to account for the censoring at zero.
Figure 1 – Ordinary linear regression model for censored data
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following worksheet array function starting in Rel 9.2 where Rx is an n × k array containing the X data and Ry is an n × 1 array containing the Y data.
TobitCoeff(Rx, Ry, iter, prec, Rg): returns a k+3 × 2 array whose first k+1 rows contain the estimated Tobit regression coefficients b0, b1, …, bk (in column 1) and the standard errors for these coefficients (in column 2). Row k+2 contains the estimate for σ and its standard error. The last row contains the value of LL for the model with these coefficients (in column 1) and the number of iterations for convergence (in column 2).
Here iter = the maximum number of iterations (default 100) and prec = the value sufficient for convergence, which is when the sum of the squares of the values in is less than prec (default 0.000001).
Rg is an optional k+2 × 1 array or cell range containing the initial guesses for the regression coefficients b0, b1, …, bk, and σ. If this Rg is omitted it defaults to n/n1 times the OLS regression coefficients estimates, from the formula =RegCoeff(Rx, Ry), and n/n1 times the OLS estimate for σ, from the formula =RegSE(Rx, Ry) where n1 = the number of observations in Ry where y > 0.
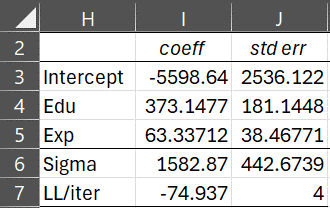
For Example 1, the array formula =TobitCoeff(A2:B18,C2,C18) produces the array shown in range I3:J7 of Figure 2.
Figure 2 – TobitCoeff
We see that this estimate converged in 4 steps, minimizing LL at -74.937.
As usual, we can obtain the AIC and BIC/BSC values for Example 1 as follows where n = 17 and k = 2.
AIC = -2*LL+2*(k+2) = 157.874
BIC = -2*LL+LN(n)*(k+2) = 161.2068
Since there are k = 2 independent variables (Edu and Exp) the total number of parameters is k+2 = 4 (including the intercept and sigma).
More Worksheet Functions
Real Statistics also provides the following worksheet function.
TobitLL(Rx, Ry, Rc) = LL for the Tobit regression coefficients in the k+2 × 1 column array Rc where Rx and Ry are as described above.
For Example 1, the formula =TobitCoeff(A2:B18,C2,C18, I3:I6) returns the value -74.937.
Finally, Real Statistics also provides the following worksheet array function.
TobitPred(Rx0, Rc): returns an m × 2 array containing the forecasted values for the X values contained in the m × k array Rx0 based on the Tobit regression coefficients in the k+2 × 1 column array Rc. Here, the first column contains the uncensored (mean) predictions, and the second column contains the censored predictions.
Example continued
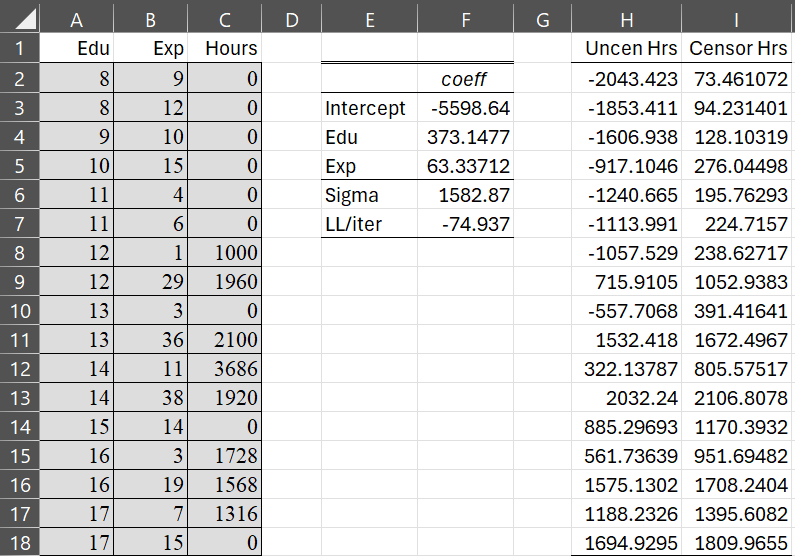
For Example 1, the array formula =TobitPred(A2:B18, I3:I6) produces the output shown H2:H18 of Figure 3. Here, A2:B18 contains the original X data and I3:I6 contains the regression coefficients from the Tobit model.
Figure 3 – Mean uncensored and censored values
For example, for a woman with 8 years of education and 9 years of work experience, the mean uncensored hours of work outside the household is -2043.423, per Property 3, calculated as usual by =F3+MMULT(A2:B2,F4:F5). In fact, the values in range H2:H18 can be calculated by the array formula =F3+MMULT(A2:B18,F4:F5).
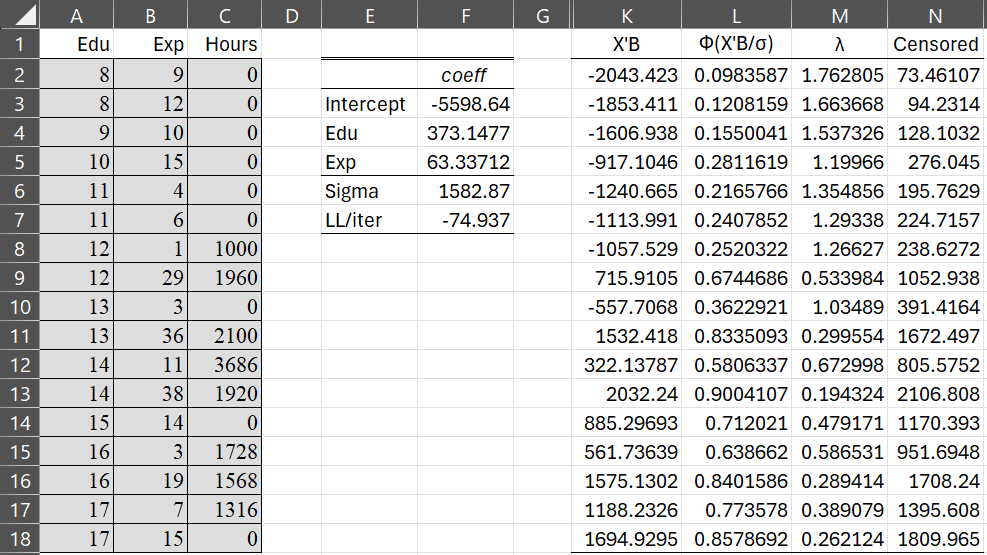
The censored values in column I are calculated using Property 5. This is shown in Figure 4.
For example, cell K2 contains the formula =F3+MMULT(A2:B2,F4:F5), cell L2 contains =NORM.S.DIST(K2/F$6,TRUE), cell M2 contains =NORM.S.DIST(K2/F$6,FALSE)/L2. And cell N2 contains =L2*(K2+M2*F$6).
Figure 4 – Calculation of censored estimates
TobitPred can also be used to calculate uncensored and censored estimates for X values that were not in the data used to create the Tobit model. This is shown in Figure 5 where R2:S2 contains the formula =TobitPred(P2:Q2,F3:F6).
Figure 5 – Uncensored and censored hours
Data Analysis Tool
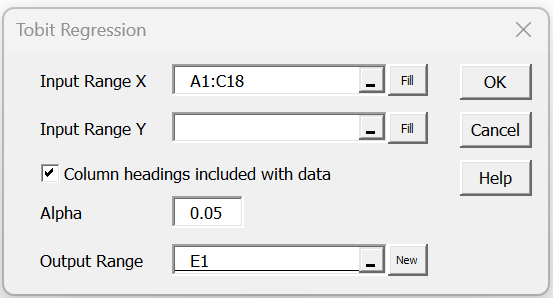
The Real Statistics Resource also supplies the Tobit Regression data analysis tool to build a Tobit model. To use this tool for Example 1, press Ctrl-m and choose the Tobit Regression option from the Reg tab (or from the Regression option if using the original user interface). Fill in the dialog box that appears as shown in Figure 6.
Figure 6 – Tobit Regression dialog box
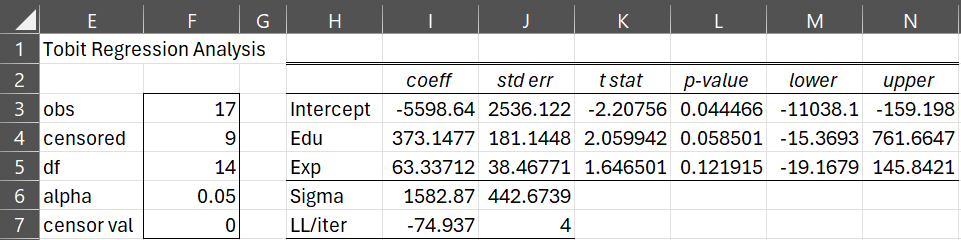
After clicking on the OK button, the output shown in Figure 7 appears.
Figure 7 – Tobit regression output
The output contains the familiar regression information based on the t static. Here the df error value is calculated as usual by n – k – 1 = 17-2-1 = 14.
References
Shanaev, S. (2021) Tobit model explained: censored regression (Excel)
https://www.youtube.com/watch?v=QS3OAYML2nM
Munk-Nielson, A. (2016) The Tobit model
https://www.youtube.com/watch?v=IwsE8Rr6l6E
Demeritt, J. (2024) Tobit model
https://jdemeritt.weebly.com/uploads/2/2/7/7/22771764/tobit1.pdf
Greene, William. 2003. Econometric Analysis. New Jersey: Prentice Hall.
Wikipedia (2024) Tobit model
https://en.wikipedia.org/wiki/Tobit_model
SAS (1999) Computing predicted values for a Tobit model
https://www.sfu.ca/sasdoc/sashtml/stat/chap36/sect24.htm