Property 1: The regression line has form
where the coefficients bm are the solutions to the following k equations in k unknowns.
Proof: Our objective is to find the values of the coefficients bi for which the sum of the squares
is minimum where ŷi is the y-value on the best-fit line corresponding to xi1,…,xik. Now,
For any given values of (x11, …, x1k, y1), …, (xn1, …, xnk, yn), this expression can be viewed as a function of the bi, namely g(b0, …, bk):
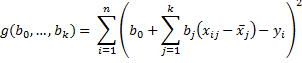By calculus, the minimum value occurs when the partial derivatives are zero. i.e.
Transposing terms we have
Further simplifying
But since 
The remaining k equations are:
These are equivalent to
Since we have k equations in k unknowns (the bm), there can be a unique solution.
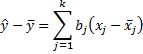
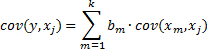
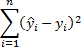
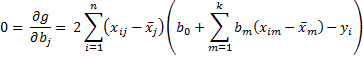
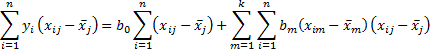
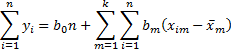
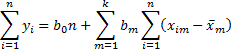
Merhaba Charles,
İstatistik ve araştırma deneme ile ilgili çok güzel site hazırlamışsınız.
Size ve ekibinize çok teşekkür eder, saygılarımla.
Ancak benim bir isteğim var. Excell hazırlanan konuların SAS veya SPSS veya Jump gibi uygulamaları var mı ?
Best Regards
Hakkı Akdeniz
Hakki,
Thank you for your kind words about Real Statistics.
I am sorry, but I couldn’t understand your question about SAS, SPSS and Jump based on the Google Translate translation.
Charles
I believe where you have the function g derivative to b_{0}, after the summation over index m, the b_{j} should be b_{m}.
Hello GJ,
Yes, you are correct. Thank you for catching this error. I have now corrected the webpage.
I appreciate your help in improving the accuracy of the Real Statistics website.
Charles