Introduction
We can use the method described in Goodness of Fit to determine whether two sets of data are independent of each other. We organize the data in what are called contingency tables, as described in Example 1. In these cases df = (row count – 1) (column count – 1).
Excel worksheet function
Excel Function: The CHISQ.TEST function described in Goodness of Fit can be extended to support ranges consisting of multiple rows and columns. For R1 = the array of observed data and R2 = the array of expected values, we have
CHISQ.TEST(R1, R2) = CHISQ.DIST(x, df) where x is calculated from R1 and R2 as in Definition 2 of Goodness of Fit and df = (row count – 1) (column count – 1).
The ranges R1 and R2 must have the same size and shape and can only contain numeric values.
For versions of Excel prior to Excel 2010, the CHISQ.TEST function doesn’t exist. Instead, you need to use the equivalent function, CHITEST.
Example using CHISQ.TEST
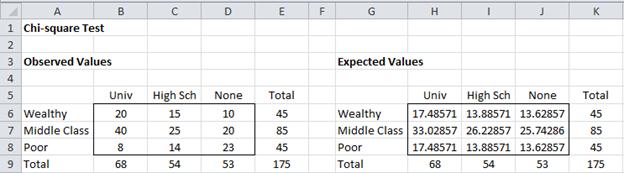
Example 1: A survey was conducted of 175 young adults, classifying their highest level of schooling as graduated from university, graduated from high school, or neither, and classifying their parents as wealthy, middle class, or poor. The results of the survey are summarized on the left side of Figure 1 (Observed Values). Based on the data collected can we conclude that a person’s level of schooling is independent of their parents’ wealth?
Figure 1 – Observed data and expected values for Example 1
The null hypothesis is
H0: The highest level of schooling attained is independent of parents’ wealth
We use the chi-square test, and so need to calculate the expected values that correspond to the observed values in the table above. To accomplish this we use the fact (by Definition 3 of Basic Probability Concepts) that if A and B are independent events then P(A ∩ B) = P(A) ∙ P(B). We also assume that the proportions from the sample are good estimates for the probabilities of the expected values.
Expected Values
We now show how to construct the Expected Values shown in Figure 1. Since 45 of the 175 people in the sample are from wealthy families, the probability that someone in the sample is from a wealthy family is 45/175 = 25.7%. Similarly, the probability that someone in the sample graduated from university is 68/175 = 38.9%.
Based on the null hypothesis, the event of being from a wealthy family is independent of graduating from university, and so the expected probability of both events is simply the product of the two events, or 25.7% ∙ 38.9% = 10.0%. Thus, based on the null hypothesis, we expect that 10.0% of 175 = 17.5 people are from a wealthy family and have graduated from university.
In this way, we can fill out the table for expected values. We start by setting all the totals in the Expected Values table to be the same as the corresponding total in the Observed Values table (e.g. cell K6 contains the formula =E6). We then set every Expected Values cell to
(row total ∙ col total) / grand total
E.g. cell H6 contains the formula =K6*H9/K9. An alternative approach for filling in all the cells in the Expected Values table is to place the following array formula in range H6:J8 (and then press Ctrl-Shft-Enter):
=MMULT(K6:K8,H9:J9)/K9
See Matrix Operations for more information about the MMULT array function.
p-value
We can now calculate the p-value for the chi-square test statistic by using a formula of form =CHISQ.TEST(Obs, Exp, df) where Obs is the 3 × 3 array of observed values, Exp = the 3 × 3 array of expected values and df = (row count – 1) (column count – 1) = 2 ∙ 2 = 4. Since
CHISQ.TEST(B6:D8, H6:J8) = 0.003273 < .05 = α
we reject the null hypothesis and conclude that the level of schooling attained is not independent of parents’ wealth.
Example using CHISQ.DIST.RT or CHISQ.INV.RT
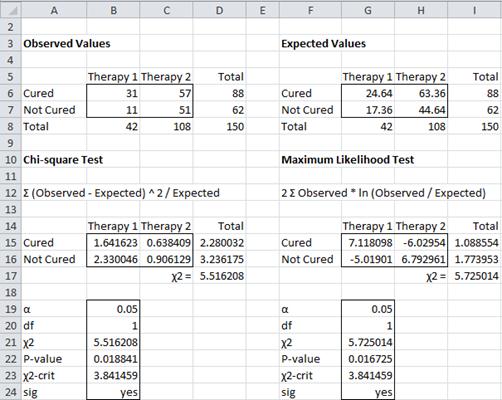
Example 2: A researcher wants to know whether there is a significant difference between two therapies for curing patients of cocaine dependence (defined as not taking cocaine for at least 6 months). She tests 150 patients and obtains the results in the upper left part of the table below (labeled Observed Values).
Figure 2 – Chi-square tests for independence
We establish the following null hypothesis:
H0: There is no difference between the two therapies’ ability to cure cocaine dependence
We next calculate the Expected Values from the Observed Values and then the p-value of the chi-square statistic as we did in Example 1. This time, however, we will use the approach employed in Example 2 of Goodness of Fit, namely calculating the Pearson’s chi-square test statistic directly (using Definition 2 of Goodness of Fit). The value of this statistic is 5.516 (cell D17 in Figure 2). Since we are dealing with a 2 × 2 table of observations, df = (2 – 1)(2 – 1) = 1. Finally, we observe that
p-value = CHISQ.DIST.RT(χ2, df) = CHISQ.DIST.RT(5.516,1) = .0188 < .05 = α
χ2-crit = CHISQ.INV.RT(α, df) = CHISQ.INV.RT(.05,1) = 3.841 < 5.516 = χ2-obs
and so, based on either of these results, we reject the null hypothesis and conclude there is a significant difference in the cure rate between the two therapies.
Using the maximum-likelihood test
As mentioned in Goodness of Fit, the maximum likelihood test is a more precise version of the chi-square test. The lower right-hand side of the worksheet in Figure 2 shows how to calculate the maximum likelihood statistic (using Definition 1 of Goodness of Fit). The value of this statistic is 5.725, which is not much different from the test statistic we obtained using Pearson’s version of the test. Since this statistic is also approximately chi-square with one degree of freedom, the analysis is quite similar:
p-value = CHISQ.DIST.RT(χ2, df) = CHISQ.DIST.RT(5.725,1) = .015 < .05 = α
χ2-crit = CHISQ.INV.RT(α, df) = CHISQ.INV.RT(.05,1) = 3.841 < 5.725 = χ2-obs
and so once again, we reject the null hypothesis and conclude there is significant difference in the results for the two therapies.
Observation: It is very important to include all observations in the test. E.g. if in Example 2 we only test Cured vs. Therapy 1 and 2, we would get erroneous results. We need to include Not Cured as well as Cured.
Real Statistics Functions
Real Statistics Functions: The Real Statistics Resource Pack furnishes the following worksheet functions where R1 and R2 are arrays containing only numerical values:
CHI_STAT2(R1, R2) = Pearson’s chi-square statistic for observed values in R1 and expected values in R2.
CHI_MAX2(R1, R2) = Maximum likelihood chi-square statistic for observed values in R1 and expected values in R2.
CHI_STAT(R1) = Pearson’s chi-square statistic for observed values in R1.
CHI_MAX(R1) = Maximum likelihood chi-square statistic for observed values in range R1.
CHI_TEST(R1) = p-value for Pearson’s chi-square statistic for observed values in range R1.
CHI_MAX_TEST(R1) = p-value for Maximum likelihood chi-square statistic based on the observed values in R1.
Note that CHI_STAT(R1) is equivalent to CHI_STAT2(R1, R2) where R2 is an array containing the expected values calculated from R1. With R2 defined in this way, CHI_MAX(R1) is equivalent to CHI_MAX2(R1, R2) and CHI_TEST(R1) is equivalent to CHISQ.TEST(R1, R2).
Data Analysis Tool
Real Statistics Data Analysis Tool: The Real Statistics Resource Pack provides a Chi-Square Test for Independence data analysis tool.
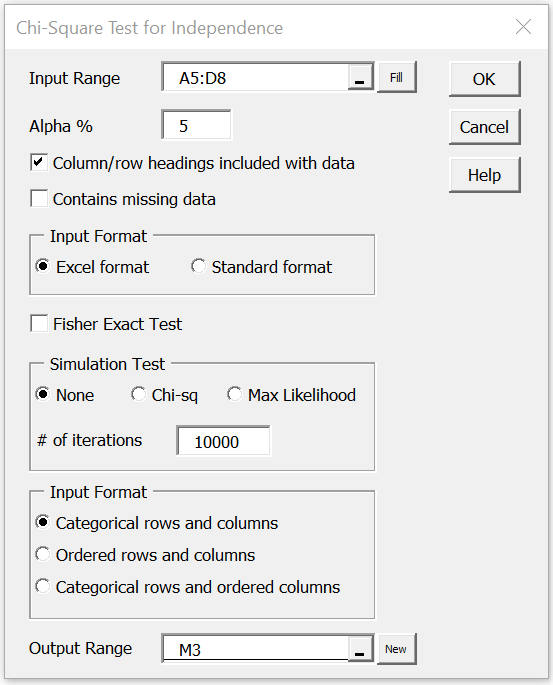
To use this tool for Example 1, press Ctrl-m and select the Chi-square Test for Independence option from the menu that appears (or from the Misc tab if using the Multipage option). A dialog box then appears as shown in Figure 3.
Figure 3 – Dialog box for Chi-square Test
Insert the observed data range into the Input Range, excluding the totals, but optionally including the row and column headings (i.e. range A5:D8), click on the Excel format radio button and press the OK button. Leave the Fisher Exact Test option unchecked (see Fisher Exact Test for use of this option) and retain the remaining default settings.
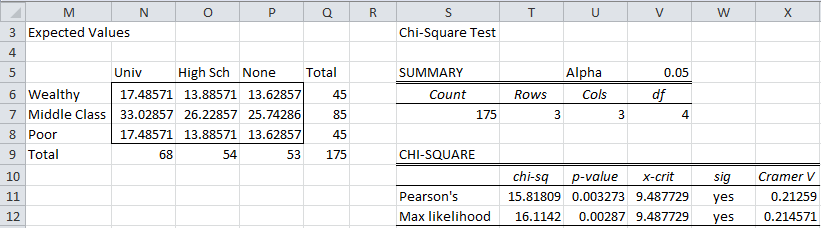
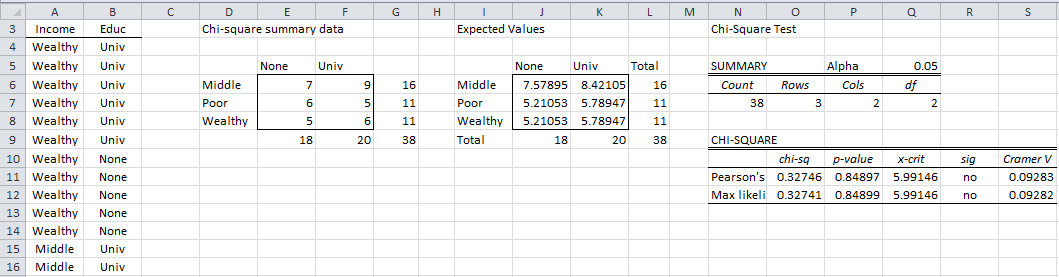
The data analysis tool builds an array with the expected values and performs both the Pearson’s and maximum likelihood chi-square tests. Cramer’s effect size, and for 2 × 2 contingency tables the Odds Ratio effect size, as described in Effect Size for Chi-square are also calculated. The output from the data analysis tool for the data in Example 1 is shown in Figure 4.
Figure 4 – Chi-Square data analysis tool output for Example 1
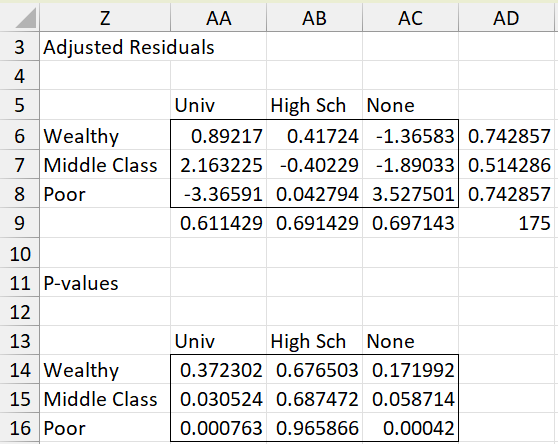
The data analysis tool also outputs the adjusted residuals displayed in Figure 4a. These are described in Independence Testing Follow-up.
Figure 4a – Data analysis tool adjusted residuals
Minimum cell size
As described in Goodness of Fit, the expected frequency for any cell in the contingency table should generally be at least 5. With small tables (especially 2 × 2 tables), cells with expected frequencies of at least 10 would be preferable.
For large contingency tables, a small percentage of cells with an expected frequency of less than 5 can be acceptable. Even for smaller contingency tables having one cell with an expected frequency of less than 5 may not cause big problems, but it is probably a better choice to use Fisher’s Exact Test or the Simulation Chi-square Test in this case. In any event, you should avoid using the chi-square test where the expected frequency in any cell is less than 1.
A less conservative and reasonable rule-of-thumb is to accept at most 20% of the cells with expected frequencies of less than 5, but none less than 1.
If the expected frequency for one or more cells is less than 5, it may be beneficial to combine one or more cells so that this condition can be met, although this must be done in such a way as to not bias the results.
Standard input format
In addition to the usual Excel input data format, the Real Statistics Chi Square Test data analysis tool supports another input data format called standard format. This format is similar to that used by SPSS and other statistical analysis programs.
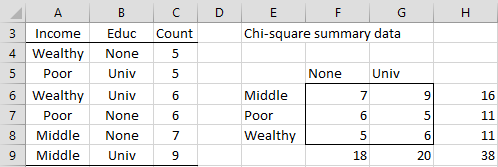
Example 3: A survey was conducted of 38 young adults whose parents are classified either as wealthy, middle class, or poor to determine whether they will graduate from university or not. The results are summarized on the left side of Figure 5 (only the first 13 of 38 rows of data are shown). Based on the data collected is a person’s likelihood of graduating from university independent of their parents’ wealth?
Figure 5 – Data and chi-square tests for Example 3
Once again enter Ctrl-m and select the Chi-square data analysis tool. When the dialog box shown in Figure 3 appears, insert A3:B41 into the Input Range, click on the Standard format radio button, and press the OK button.
The data analysis tool first builds a contingency table (range D5:F8 of Figure 5) and performs the same type of analysis as for Examples 1 and 2. Since sig = no (cells R11 and R12) we cannot reject the null hypothesis that a person’s graduating from university is independent of their parents’ level of wealth.
Three-column standard format
Example 3 uses the two-column version of the standard format. There is also a three-column version, which is a frequency table version of the other standard format. We demonstrate this in Figure 6 where A4:C9 is inserted in the Input Range (or A3:C9 if the Column/row headings included with data option is checked). The output is identical to that shown in Figure 5.
Figure 6 – Standard format
Post-hoc Testing
After a significant result from the chi-square test of independence, you can perform one of several follow-up tests to pinpoint the cause of the significant result. Further information about this topic can be found by clicking on the following links:
Missing Data
When some of the data in the contingency table is missing, we can still conduct an independence test, as described at
- Independence test with missing data
- Real Statistics support for independence testing with missing data
Tests with Ordinal Categories
The chi-square test of independence described on this webpage assumes that both the rows and columns of the contingency table contain counts of nominal (categorical) categories. When one of the categories is nominal and the other is ordered (ordinal), then we can use the following alternative test which takes the order into account.
When both categories are ordered, you can use the following test:
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
Dr. Zaiontz,
Let the null hypothesis be: variable A is independent of variable B. If Chi-square independence test’s p-value is greater than alpha, then it fails to reject the null hypothesis. So that means there’s collinearity between these variables? Thanks!
Hi Jim,
(a) If A and B are independent then corr(A,B) = 0.
(b) If A and B are collinear then corr(A,B) = +1 or -1
Clearly (a) doesn’t imply (b)
Charles
What is the reference for this table you referred to for interpretation of effect size df 1-5
please
Hello Rebecca,
I assume that you are referring to Figure 1 on https://real-statistics.com/chi-square-and-f-distributions/effect-size-chi-square/.
I have added two references to that webpage that contain the references to the table.
I believe that the table is equivalent to
V√df* = .1 represents a small effect, = .3 represents a medium effect and = .5 represents a large effect, which are the usual guidelines for the correlation coefficient.
Charles
thank you for the information
Thanks! It’s done!
Do you think it is necessary to apply Holm’s correction?
Hi Laura,
Since you are only doing one test, I don’t see why you would need to use Holm’s correction.
Charles
Hi Charles.
I need to prove if the data 780:260:245:85 follow the relation 9:3:3.1. Can I test it with the contingency table tool?
Thanks a lot.
Hi Laura,
You can use Excel’s CHISQ.TEST function. The actual range is the range that contains the 780:260:245:85 data, The expected range is based on the 9:3:3.1 values scaled up to the same size as the actual data, i.e. multiply by (780+260+245+85)/(9+3+3+1).
Charles
Charles
I post my inquiry here since Comments are disabled in the Chi-square Post-hoc Functions page.
I do not understand how to run any of the post-hoc tests using the RS add-in.
What/where is the function(s) that I need?
Thanks in advance.
Hello Carlo,
I don’t know why the Comment field does not appear since I enabled it.
In any, the Real Statistics for post-hoc testing are described at:
Chi-square Post-hoc Functions
You use these functions just like any of the standard, built-in Excel functions.
Charles
Are you not taking comments on the Post-hoc testing after chi-square independence testing section? I apologize if this is out of place.
I’m just having issues getting AdjRes to work on Mac.
The StdRes is working fine.
Hi Nathan,
Thanks for bringing the issue about no comments on the “Post-hoc testing after chi-square independence testing” webpage to my attention. Comments for this webpage are indeed enabled, but as you have said no comments prompt appears on this page. I don’t know why I am having this problem. In any case, I will respond to your comment shortly.
Charles
Hi Charles,
I am doing a study in a hospital on colonoscopies. We want to see if three different dependent variables (caecal intubation rate, amount of sedation and polyp detection) are affected by the day of the week. I am not sure however, how to calculate what the expected values would be as a different number of colonoscopies are done on each day and there are different percentage rates of success for each day. If you have any advice that would be great!
Thanks,
Alice
One approach is to perform three separate chi-square tests of independence, one for each of the dependent variables. This assumes that your data is in the correct form for the chi-square test of independence.
Charles
Hi, charles
I am not quite sure how to find the difference in food preferences between under- and post-graduate students in my following data set.
Year of study Favourite food
Pizza Baked potatoes Pasta Salads Chips Noodles Paninis
1st year undergrad 31 45 34 13 108 30 1
2nd year undergrad 26 5 17 9 46 58 6
3rd year undergrad 23 49 15 2 17 19 2
Post graduate 7 47 6 4 24 16 9
I have already done the expected results of the data set above.
See Post-hoc Testing at the bottom of this webpage.
Charles
Hello, I am trying to run a Chi-Square Test for Independence using the Example workbooks. I want to see the summary output. I select just the data, no columns, 0.05 alpha, Excel format, specific cell for Output Range. I always get an error box about a random number generation where an integer between 1 and 7 needs to be entered. I cannot get rid of the error box and have to shut down my computer to restart Excel. Has this happened before? Is there a bug?
Thank you
Hello Ed,
When you say that you get an error box about random number generation, are you seeing the dialog box for Excel’s Random Number Generation data analysis tool? This is shown in Figure 1 of https://real-statistics.com/sampling-distributions/simulation/
I have seen an error similar to this one during software testing when I had too many spreadsheets open at the same time or one spreadsheet that required a lot of processing or memory (such as a couple of the Real Statistics Examples workbooks). This shouldn’t happen ordinarily. When this has happened, I just keep hitting the Enter key until the Excel data analysis tool closes. This may take awhile. You can also press Ctrl-Alt-Del and try to shut down Excel (without having to shut down your computer). Make sure that you don’t have some other big resource-consuming Excel spreadsheet open when you restart Excel, otherwise the problem will repeat.
Charles
Hi Charles,
as a follow up on the Chi Square test: I’ve established in a 5×4 table (both variables nominal) a significant relation between the two variables. I made an observed table, an expected table and a (observe-expect)^2/expect table.
Now I know that, I’d like to dive a bit deeper: are there certain factors that cause this? I can see that in my last table, there are several values that are big and cause a high Chi value. So I could e.g. conclude: row2&column3 has a much higher observed value than expected value. Or: the biggest contributors to this significant relation are a much higher observed than expected row2&column3 and row2&column4. That feels a bit weak.
I bumped into “Column Proportion tests” and saw some pointers from SPSS and another online tool:
https://www.ibm.com/support/knowledgecenter/en/SSLVMB_24.0.0/spss/tutorials/xtab_crosstab_demo_col_proportion.html
https://help.surveygizmo.com/help/cross-tab-report#understanding-column-proportion-testing
https://www.reddit.com/r/AskStatistics/comments/2deny8/interpreting_spss_chi_square_output/
All quite interesting, but I am struggling where to start building this in Excel (am fluent in excel,vba,matrix formulae, you name it), do you have some pointers?
Thanks!
Hello,
Have you found that the chi-square test gives a significant result based on a 5×4 contingency table (i.e. the two variables are not independent and now you want to do some follow-up analysis to determine what is causing the significant result?
Charles
Exactly, I have about 1000 rows in my data table, made the 4×5 crosstab with observations etc (one question has 4 possible answers, the other has 5 possibilities). They are indeed not independent as I found out with a Chi square test.
Hello,
I have been thinking about updating this webpage to address this very issue. You have now given me a good excuse for doing this.
I will work on this shortly.
Charles
Hi Charles, that sounds wonderfull. I am looking forward to it. Thanks a million in advance!
Hi Charles,
as an addition: I’ve built up some cases in Excel, starting with your Chi example, adding a Bonferroni example and now working on the columns comparing example.
https://www.dropbox.com/s/d378g1z2tsqacox/chi_bonf_col_tests.xlsx?dl=0
The main issue I have in this example is finding the critical value, corrected with Bonferroni, see the yellow cells from row 55 down. Hints are welcome and feel free to take that example to include on your site.
Cheers,
Koen
Hi Koen,
I have developed some new software to deal with these sorts of issues. I plan to include it in the next release of Real Statistics. This should be available in the next couple of days.
Charles
I’m curious to check it out! I’ve modified my example file thanks to a For Dummies manual I found. Good to refresh this knowledge! I’ve added a simple column wise comparison and think I’ve got the whole calculation working (my whole sheet is still macro-free). Very interesting to check it vs your release.
I just want to thank you for this useful, intuitive and good statistical tool!
Thanks!
Hi Charles….I need your help.
I have collected data based on the likert items and coded them extremely concerned =5, and not concerned = 1. I have these groups who answered the question, gender, age, place of residence. I want to do statistical analysis on these data to see if the answers are dependent on gender, age, residence, etc.
What statistical method is most applicable?
It really depends on the details, but you might be able to use multiple chi-square tests of independence, one for gender, another for age, etc. The trouble with this approach is that you won’t be taking the order from the Likert scale into account.
Charles
Hi,
I am doing a search with constructive defects where I have many defect categories around 15.
I want to associate these defect categories with their recurring behavior.
In this way, I have the occurrence frequency of defects and I know when the occurrence of the defect was recurrent or not.
is a contingency table 15×2
I have many observed frequencies smaller than 1 or 5 ..
Can I take these categories out of the analysis or do I need to group them?
Jordana,
Generally you would group categories (in a way that shouldn’t purposely bias the outcome) if the expected frequencies are less than 5 (and especially if the expected frequences are less than 1 or 2).
Charles
The Real Statistics Resource Pack does have built-in chi-square testing functionality. You can use the Chi-square data analysis tool as described at
https://real-statistics.com/chi-square-and-f-distributions/independence-testing/
Hi, I followed your method in example 1, but when I ran the CHISQ.TEST I got 0 as my answer. I used this in Excel 18, and I want to see if incomes based on a bachelor’s degree, associate’s degree, or just a high school diploma are independent from region in the U.S. The regions are northeast, midwest, west, and south. The income based on the degrees are my columns, while the locations are my rows. In each intersection I have 3 values of incomes from data I found. My question is what am I doing wrong because I keep getting either 0 or 1. This is the first time I have used Excel for statistical work, and the internet has not been helpful because I have a Mac with Excel 2018. What do you think my problem is?
Colin,
If you send me an Excel file with your data and results, I will try to figure out what is happening.
Charles
Hi Dr. Zaiontz,
Huge thanks for creating this resource pack and website, it has helped me with many projects. I’ve been using RealStats without any bugs for a few years but recently tried it on a different computer that I keep in my office. I noticed that the RealStats output for chi-squared test for independence was different than my previous analysis and I performed it manually to check. The RealStats value was definitely wrong, after troubleshooting, it looks like all of the formulas are right but for some reason, the calculated expected values matrix is wrong.
My observed values are a simple 2×2 table:
10 22
142 77
The expected values should be something like
19.3 12.6
132.6 86.4
But the RealStats output is
76 76
76 76
The problem is that though the formulas for the matrix are correct, they are not giving the right sums across the rows and columns. So instead of totals
32
219
152 99
RealStats is giving me
32
32
152 152
Again, the formulas in the defective cells are correct (e.g., sum(A1:A2) and sum(A1:B1)) but it looks to me like Excel is just not performing the second bit of sums before creating the matrix and going through with the rest of the test.
Please let me know what you think, I’m reluctant to use more complex operations until I figure out what’s screwing up this function. Thanks!
Sam,
I just ran the Chi-Square Test for Independence data analysis tool, and it returned expected values of
19.378..12.622
132.62..86.378
which I believe are similar to what you expected. The p-value = .000282.
I don’t know how you got the strange values that you reported.
Charles
Helo sir, i am having my thesis right now and i need to apply the Pearson’s Chi Square test for association for me to find out if there a significant relationship between the student’s competencies and their Science curriculum in high school. Can you please help and teach me how to compute for it? Thank you very much and god bless more.
Greetings! I think I already know the answer to this question, but I’d like to make sure I am not missing something that would make my life easier. I am using Chi Square (or Fisher’s) to test whether two treated groups had a different outcome from controls. If/when I get a p<0.05, I think I have to go back and do the test over again as a 2×2 test in order to find out which group is different (or it could be both groups, of course). Is that correct? Thanks in advance.
Donna
Donna,
You don’t have to do this sort of follow up testing, but you can do so if you need the extra information. Note that if you perform multiple follow up tests then you need to take familywise error into account. This is explained at
Experiment-wise error
I will be adding more information about this topic shortly.
Charles
Thanks!
In a chi square test of independence, can these two statements be used interchangeably? That is, are these two statements correct? Thank you!
”The GDP per capita is not independent of the fertility rate of married female”
“The GDP per capita is dependent of the fertility rate of married female”
Hye, i’m doing my research about correlation between breast density and missed cancer. We have total number of missed cancer cases and each missed cancer case got score for breast density. So how to calculate the expected value? It’s possible to use chi square?
Nur,
If you know the breast density for each missed cancer case, to get the expected score then just calculate the mean (i.e. average) of the breast density scores. You can use Excel’s AVERAGE function to calculate this. This doesn’t involve correlation or chi-square.
If you want to calculate the correlation between breast density and missed cancer, then I assume that you have breast density values for non-missed cancer cases as well. In this case you can use Excel’s CORREL function to calculate the correlation.
You mention chi-square, but you need to first identify what hypothesis you are testing.
Charles
Good day! We’re doing a thesis regarding stress, stressors, and coping strategies of students, and we used three likert scale questionnaires for each variable. The stress level questionnaire has 10 items, for stressors has 40 items, and for coping has 28 items. And I’m confused of what to do, because I asked one of our professors what to do and told us to do a Chi square to our study. I’m somehow not familiar with it. Can someone help us? Thank you!
Jean,
What to do depends on what hypothesis you want to test.
Are you trying to show that levels of stress, stressors and coping are independent of each other? (presumably this is not true)
How many people have filled in the three questionnaires? Does every participant fill in all three questionnaires?
Charles
what should I do if the maximum likelihood, chisq. results to #value in excel 2010
Ana,
It depends on why you are getting this error value. Most likely it is because one of the cells in the contingency table has a zero value. In this case, LN(0) results in the error value.
The chi-square test of independence should not be used in a case where one cell has a value of zero. You could try using the Fisher Exact test in this case.
Charles
Hi Charles,
Thank you so much for your reply. I apologise for the vagueness, My understanding is that the chi-square curve is based on the sum square of independent normal variables. Therefore, I cannot apply it to categorical data. For instance, if the X is the variable with values of 1,2,3,4,5 for Excellent, Good, Fair, Unsatisfactory, Poor, The distribution of the values of X is not a normal distribution.
In my case, I am doing a thesis which in part deals with the partition of an integer into positive summands for natural sequences such as pi and robotic sequences generated by computers. The number 6 can be decomposed 10 partitions of 6, 5+1, 4+2, 4+1+1. 3+3, 3+2+1, 3+1+1+1, 2+2+2, 2+2+1+1, 2+1+1+1+1,1+1+1+1+1. It is possible to calculate the probability for each partition. I would like to analyse the observed probabilities against the actual. At the moment, I am choosing to analyse it by confidence interval using Z score. Your comments would be very welcomed.
By the way, I found your documents on Q-Q plot, chi-square and Kutosis very helpful indeed.
Thank you again
Tong,
What you are trying to do is somewhat similar to the process required for the Wilcoxon’s Signed Ranks Exact Test
https://real-statistics.com/non-parametric-tests/wilcoxon-signed-ranks-test/wilcoxon-signed-ranks-exact-test/
Charles
Charles,
My understanding of chi-square is that the distribution of the population needs to be Gaussian and therefore rules out categorical data. In the problem that I am working on, the population distribution is categorical and the mean and Standard deviations can be calculated. I need to compare it with the distribution of a number of datasets. Is the approach to calculate the z-score of the dataset based on known mean and standard deviation to establish the confidence interval? Are there other probabilistic approaches?
Many thanks in advance,
Tong,
The chi-square test of independence deals with categorical data, and so I am not sure I understand your concerns.
What specifically are you trying to accomplish? Are you testing independence or are you trying to see whether some data fits a specific distribution or something else?
Charles
The theory of the chi-squared test is based upon the Poisson count distribution and the (related) Multinomial count distribution. In large samples, statistical tests based upon these distributions can be approximated by a Multivariate Normal distribution. And finally, the Chi-Squared distribution describes the sum of squares of normally distributed variables. Thus …. by a series of logic steps, it is completely valid to use the Chi-Squared distribution to test hypotheses with count data. That is, the Chi-Squared distribution can be viewed as a convenient way of developing a statistical test for independence in count data when the total number of counts (number of people) is large.
Gary,
Thanks for sharing this.
Charles
i am doing a research.
i have used likert scale from strongly agree to strongly disagree for each of my questions.
therefore, my degree of freedom is 16. i am trying to show chi-square test of independence for my variables from survey data. i am using SPSS 20. my chi square test values are coming like 5.18, 10.466 , 15.34 like this. now , i would like to know.what should be the interpretation of this. is it dependent or independent. for 95% confidence level for degree of freedom 16 x square is 7.962. so, below 7.962 is independent or what? i just want to know.
Sorry, but I don’t use SPSS. The referenced webpage describes when the chi-square test yields a significant result.
The following webpage describes how to calculate a 95% confidence interval:
https://real-statistics.com/chi-square-and-f-distributions/one-sample-hypothesis-testing-variance/
Charles
Hi Charles
Does Excel have frequency limits in cells when calculating Chi2.test? I have some cells with several hundred thousands and just under 3 million.
Rod,
You should be able to perform chi-square test of independence even with large cell values. Just try it!
Charles
Very interesting! I had never understood why (obs-exp)^2/exp had a z^2 distribution!
In example 2, could we also use the test for the difference between two proportions?
What are the benefits of each method?
Thanks!
Fred,
See the following webpages:
https://real-statistics.com/correlation/dichotomous-variables-chi-square-independence-testing/
https://real-statistics.com/correlation/dichotomous-variables-t-test/
Charles
i’m doing a educational reasearch called how significally change the trained and untrained teacher’s attitude relavent to the technology intergration.but nw i cant think how i used the chi squre test for items.do i check the chi square for each statements with likerts scale?
hi…i want to calculate chi sq. for bmi categories among males and females
how shall i proceed?
Sweta,
This is explained on the referenced webpage. Do you have a specific question?
Charles
ohh okay….thanks for the help.
Hi Charles,
Thanks so much for the helpful website. I am comparing two methods of treatment for acid mine drainage and have already come to the conclusion that results from the two methods are from the same population using Mann-Whitney testing. One aspect of the data I am keen on knowing though is there a difference in pass/fail rates of the resulting water quality values for the two methods. As I have already determined the methods produced results from the same population, is it then unreasonable to use this method which indicates that they produce significantly different pass/fail results?
Thank you.
Simone,
Without more information, I can’t say for sure, but Mann-Whitney is commonly used for these sorts of problems.
Charles
I have a simple question. I’m using the CHISQ.TEST function for a Chi Square test. The explanation claims that the function returns the Chi Square statistic and the degrees of freedom. But the only output I get is the P value.
How do I get the rest of the output? Or, how do I translate the P value into a Chi Square value and degrees of freedom?
Mike,
CHISQ.TEST only calculates the p-value. The webpage says that CHISQ.TEST(R1, R2) = CHISQ.DIST(x, df), and the right hand side is a p-value.
To get the chi-square statistic and degrees of freedom:
df = (# of rows in R1 – 1)(# of columns in R1 – 1)
chi-sq stat can be calculated manually as described on the Goodness of Fit webpage or by using the Real Statistic function CHI_STAT2(R1,R2) or CHI_STAT(R1).
Charles
You’ll need to calculate the df by hand (see Charles comment) but to get the chi sq test statistic use CHISQ.INV.RT(p-value, df). I don’t know why excel made it backwards but I checked it against hand calculations and it’s correct (because I did the hand calculations first and then realized there was an inverse function, d’oh).
p value is 3.28678E-14 . WHAT DOES IT MEAN. PLZ TELL
Rejesh,
This is a number written in scientific notation, i.e. 3.28678 x 10^(-14). This is a very small number, almost zero.
Charles
how to calculate likert data in chi-square test ?
suppose we take standard likert scale 1-5.
plz show me with example.
Rosshan,
Please be more specific. Perhaps you could provide an example that you are trying to solve.
Charles
Hello: I am trying to analyze whether patient feedback influences a doctor to recommend a certain treatment.
The data I have is “are you likely to recommend treatment X” (3 rows: yes, somewhat, no) and “did you receive positive feedback about treatment X from your patients” (3 columns: yes, no, don’t know). The data is below. I did a chi-test analysis with a p-value of 0.43.
5 1 2
8 0 5
2 1 4
The other data I have is “are you likely to recommend treatment X” (3 rows: yes, somewhat, no) and “did you receive negative feedback about treatment X” (3 columns: yes, no, don’t know). Data below. The chi-test p value I got is 0.07.
1 5 2
6 4 3
1 1 5
I would conclude that neither positive or negative feedback influences docs to recommend treatment X, but want to make sure the chi-test is the right one to use?
Tanya,
Each chi-square test seems reasonable.
Charles
Hi Charles,
So I have a problem. I need to cross the variable “field of profession” with a yes/no question in SPSS. The problem is that when i do cross this variables I get that 42.9% have expected count less than 5, which means the test isn’t valid. Since my table is 7×2 I can´t read the results from Fisher’s Test. What can I do? Is it ok to combine some fields of profession (rows)..for instance..is it ok to combine phisician with nurse in the same row? Doesn’t this change the results?
Thanks
Yes, you can combine rows or columns of cells to get a cell count which is sufficiently large.
Charles
Hello,
May I know Chi-square test for homogeneity.
e.g. Null Hypothesis : P1=N1 and P2=N2 and P3=N3
Alternative Hypothesis:
P1 is not equal N1 or
P2 is not equal N2 or
P3 is not equal N3
If we reject Null Hypothesis. There we have to find for 95% CI for each proportion so that we can prove which pair is not equal in reality. For this case how can we calculate by using Excel. Could you please explain me? Thanks
Yan Win Soe,
Are you referring to three-way contingency tables? If so, please see the following webpage:
Log-Linear Regression
Charles
Hello Charles,
Kindly clarify this for me;
How do you treat statistical significance tests using age ranges or years of experience.
say you have one group made up of managers and you want to establish each of their opinion on a process by their years of experience (7 point LIKERT).
manager = 8
years of experience: 0-3 (4), 4-6 (3), 10 + (1)
Which tests is most appropriate?
Do you take an average of each range?
Thank you.
Christine,
Sorry, but I don’t understand the situation that you are describing.
Charles
Hi Charles,
Can I used Chi square test to understand if Age or tenure has any relation to employee quitting.
So the table would have Age range in row and Resigned or Active in column
Kind regards
Shri
Hi Shri,
Yes, you can create such a 2 x 2 contingency table and use the chi-square test for independence. You didn’t seem to factor tenure into this table, though.
Charles
Hi Charles,
Thanks.
Sorry to bother with these questions. Trying to use stats for decision making in HR.
I was planning to use tenure in a separate table, comparing tenure and turnover, does that make sense.
OR
Can I use tenure and age in one table but it would not include turnover in it.
Shri,
Yes, you can do this. It all depends on what your want to test.
Charles
Hello Sir/Madam,
Can you please help give me some advices on how to conduct a Chi-Square test to understand whether the gender data from my sample dataset has any deviations from the census dataset? p>0.05 or not?
My Gender Dataset is
Male 307
Female 330
The Census Dataset is
Male 3303015
Female 3768561
It is because the SAV or Excel file in SPSS failed to add as large as over 3303015 and 3768561 and grid cells, so I am facing a headache in doing the aforesaid analysis.
Thank you very much.
I can’t comment on SPSS, but if you use the Real Statistics Chi-square data analysis tool, you will get a result, even for such large data elements.
Charles
hello!
I am trying to do a chi test on a 5*5 table but the 5th line is full of 0. the test comes invalid but when i eliminate the last line which is only 0 (it becomes a 4*5 table) it works and i get results. How should I proceed??
Sarah,
You shouldn’t use chi-square if you have cells with zero values (or even a lot of cells with values less than 5). Either you should eliminate the last row or combine it with the row above.
Charles
Charles,
I am running a 5×5 Chi square test in Excel format. I am getting my Expected Values and Summary and they look to be fine. However, I am getting an error in my chi-sq, p-value, , sig, and Cramer V for both Pearson’s and Max likelihood. The only thing showing up is my x-crit. I am running 4.4 Excel 2007.
I should mention that I have several cells that the number is 0 in my 5×5.
Thanks!!!
I had two full rows that had zeros in my 5×5. I removed them and ran it again as a 3 rows x 5 columns. This time it worked. Will this cause a bias the results or since they are zero does it matter?
Robert,
Eliminating full rows or columns with zeros is fine, but if the table that remains contain one or more cells containing a zero, then the test is not considered to be valid. You can get around this by combining rows or columns.
Charles
The test is not valid if there are cells which contain a zero.
In this case you might use the Fisher Exact Test, although the usual version of this test is for a 2 x 2 table.
Charles
Hi,I have a gene expression file which contains numerical data and has high dimension.how can I use chi test in my data for dimension reduction.thanks
I don’t yet address this subject. Here are two articles that do.
http://www.sciencedirect.com/science/article/pii/S0047259X03000563
http://www.kdnuggets.com/2015/05/7-methods-data-dimensionality-reduction.html
Charles
hi sir, please explain how i feed the data to calculate chi-square test with the help of real statistics data analysis tool?
sir, please explain with any new example of share any video for that.
please sir,
compile error in hidden module: froinput is shown again and again
The Real Statistics Chi-square data analysis tool accepts input data in either (a) Excel format (i.e. contingency table format) as shown in range A5:D8 of Figure 1 of the referenced webpage or (b) standard format (also called stacked format) as shown in Figure 5.
Regarding the compile error, please let me know the following information:
1. What do you see when you enter the formula =VER() in any cell?
2. What release of Excel and Windows are you using?
3. What language are you using (English, French, etc.)?
Charles
I like this page, it is meangfull to not only staticians but also to all researchers….
Hi Charles, you did a great job here. I would like to clarify something. Below are my data set:
134 8 3
310 282 99
1404 127 267
700 7 1
874 83 53
20 238 262
130 18 74
161 68 132
41 0 3
A total of 9 rows and 3 columns. Why is my p-value = 0. What does this mean? I hope i calculated it correctly. My p-values is zero, which makes my χ2-crit equally 0. Please help!
Anthony,
I calculated that chi-square stat = 2159.44 and p-value = CHIDIST(2159.44,16,TRUE) = 0. This means that the test is highly significant. Thus the two variables that you are testing are not independent.
It does not mean that χ2-crit = 0. In fact, χ2-crit = CHIINV(.05,16) = 26.30 (assuming an alpha value of .05). Since χ2 > χ2-crit, once again we conclude there is a significant result.
Charles
hey..
i tried this module but it shows me an error saying “compile error in hidden module: chiSquare” can u please tell me how do i solve tht error….
thanks..
When you enter the formula =VER() in any worksheet cell what result do you get? Also which version of Excel are you running?
Charles
All much too complex for my needs, which are very simple: do 40 male and 60 female fruit flies fit a 1:1 expectation at P<0.05? How do I do it in Excel? My contingency table has four columns (o, Ho, e and Chi-square) and three rows (male, female) and sum. How do I do it in Excel?
Dick,
You seem to be conducting a goodness of fit test (which is related to an independence test, but slightly different). The approach is similar to that shown in Example 3 of https://real-statistics.com/chi-square-and-f-distributions/goodness-of-fit/.
You create the following table in Excel (which is similar to the table you described):
row 1: Gender, Obs, Exp, Chi-sq (in columns A, B, C, D)
row 2: Male, 40, 50, blank
row 3: Female, 60, 50, blank
row 4: Sum, =SUM(B2:B3), =SUM(C2:C3),=CHITEST(B2:B3,C2:C3)
Charles
Charles: Except that the answer you get is incorrect: 0.046. Should be 10 squared, divided by 50, then multiplied by 2 = 4.0. What has gone wrong?
Dick,
I don’t see any example on the referenced webpage where I get an answer of 0.046. Which example are you referring to?
Charles
The example I gave you above:
row 1: Gender, Obs, Exp, Chi-sq (in columns A, B, C, D)
row 2: Male, 40, 50, blank
row 3: Female, 60, 50, blank
row 4: Sum, =SUM(B2:B3), =SUM(C2:C3),=CHITEST(B2:B3,C2:C3)
Dick,
Sorry, the formula =CHITEST(B2:B3,C2:C3) is not correct. It should be =FIT_TEST(B2:B3,C2:C3). This results in p-value = .0455.
An alternative approach is to use
row 1: Gender, Obs, Exp, Chi-sq (in columns A, B, C, D)
row 2: Male, 40, 50, =(B2-C2)^2/C2
row 3: Female, 60, 50, =(B3-C3)^2/C3
row 4: Sum, =SUM(B2:B3), =SUM(C2:C3),=SUM(D2:D3)
Thus cell D4 will contain the value chi-sq = 4 and the value of the test is given by the formula =CHIDIST(D4,1), which has value .0455.
Charles
Hello Charles!
I am looking for one statistic test for my data to find the significance or independence of variables or association between them. I made the table of cross tabulation of variables for frequency. Definitely, they are categorical variable. However, there are the values of actual (observed) counts which are equal to 0; so some values of expected counts are less than 1. How should I do in this case?
How can I test those in the following by chi-square test
Say: people have two staged choice. In the first stage, he either choose A or B. After his choice in stage 1 , he face another choice C or D. His two-staged choice could lead to two kind of results, either true or false. I want test with the combination of A+ C would lead to true results, significantly.
I’ve done a 2*4 chi-square test by listed all the combination : A+C, A+D, B+C, B+D. But it could only explain different combination have different influence toward the results. How could I know if A+C have significant influence?
Thanks
Kate,
I don’t quite understand what you are trying to accomplish. From what I understand it doesn’t seem like you are testing for independence, which is what the chi-square test for independence is designed to accomplish. How what you are testing fit with a test for independence?
Charles