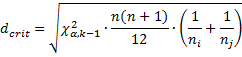Basic Concepts
The Schaich-Hamerle Test is similar to Dunn’s test, but it uses the chi-square distribution instead of the normal distribution. We calculate pairwise differences between the average ranks
using the critical value
Here n = the total sample size, ni and nj are the sizes of the groups being compared, and χ2α,k-1 is the critical value of the chi-square distribution for the given alpha and k – 1 degrees of freedom. The difference between the ith and jth groups is significant if dcrit < d.
Data Analysis Tool
Example 1: Find all significant differences between the blemish creams of Example 1 of Kruskal-Wallis Test at the 95% significant level.
To perform this test, we proceed as in Example 1 of Nemenyi Test, except that we choose the Schaich-Hammerle option instead of the Nemenyi option. When we press the OK button the result shown in Figure 1 is displayed.
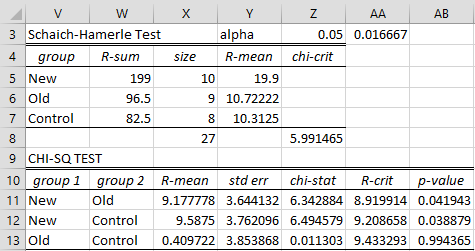
Figure 1 – Schaich-Hamerle test
If we use an alpha value of .05, then New-Old and New-Control are both significant comparisons (since the p-values are less than .05). If we use a Bonferroni correction (alpha = .01667 in cell AA3), then none of the comparisons are significant.
Most of the formulas in Figure 1 are similar to those in Figure 1 of Dunn’s Test. Cell Z8 contains the formula =CHISQ.INV.RT(Z3,COUNT(X$5:X$7)-1), cell Z11 contains the formula =(X11/Y11)^2 and cell AB11 contains =CHISQ.DIST.RT(Z11,COUNT(X$5:X$7)-1).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
NCSS (2012) One-way analysis of variance
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/NCSS/One-Way_Analysis_of_Variance.pdf