Introduction
We start our description of ANOVA with the one-factor case. We will define the concept of factor elsewhere, but for now, we simply view this type of analysis as an extension of the t-tests that are described in Two Sample t-Test with Equal Variances and Two Sample t-Test with Unequal Variances. As usual, we begin with an example which is an extension of Example 1 of Two Sample t-Test with Equal Variances.
Example
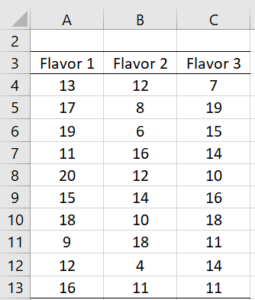
Example 1: A marketing research firm tests the effectiveness of three new flavorings for a leading beverage using a sample of 30 people, divided randomly into three groups of 10 people each. Group 1 tastes flavor 1, group 2 tastes flavor 2 and group 3 tastes flavor 3. Each person is then given a questionnaire that evaluates how enjoyable the beverage was. The scores are as in Figure 1. Determine whether there is a perceived significant difference between the three flavorings.
Figure 1 – Data for Example 1
Since the people in the study are assigned to the groups at random, this sort of experiment is said to be a completely random experimental design. We can consider the flavors are the independent variable (with three categorical values) and the scores from the questionnaires as the dependent variable.
Our null hypothesis is that any difference between the three flavors is due to chance.
H0: μ1 = μ2 = μ3
H1: μ1 ≠ μ2 or μ1 ≠ μ3 or μ2 ≠ μ3
We interrupt the analysis of this example to give some background, after which we will resume the analysis.
Basic Definitions
Definition 1: Suppose we have k samples, which we will call groups (or treatments); these are the columns in our analysis (corresponding to the 3 flavors in the above example). We will use the index j for these. Each group consists of a sample of size nj. The sample elements are the rows in the analysis. We will use the index i for these.
Suppose the jth group sample is
and so the total sample consists of all the elements
We will use the abbreviation x̄j for the mean of the jth group sample (called the group mean) and x̄ for the mean of the total sample (called the total or grand mean).
Let the sum of squares for the jth group be
We now define the following terms:
![]()
![]()
SST is the sum of squares for the total sample, i.e. the sum of the squared deviations from the grand mean. SSW is the sum of squares within the groups, i.e. the sum of the squared means across all groups. SSB is the sum of the squares between-group sample means, i.e. the weighted sum of the squared deviations of the group means from the grand mean.
we also define the following degrees of freedom
Finally, we define the mean square as
Summarizing:
Observations: Clearly MST is the variance for the total sample. MSW is the weighted average of the group sample variances (using the group df as the weights). MSB is the variance for the “between sample” i.e. the variance of {n1x̄1, …, nkx̄k}.
Properties
Property 1: If a sample is made as described in Definition 1, with the xij independently and normally distributed and with all σj2 equal, then
![]()
This property can be used to calculate confidence intervals for MST, MSB and MSW.
Property 2:
![]()
![]()
Click here for a proof of Properties 1 and 2.
Structural Model
Definition 2: Using the terminology from Definition 1, we define the structural model as follows. First, we estimate the group means from the total mean: = μ + aj where aj denotes the effect of the jth group (i.e. the departure of the jth group mean from the total mean). We have a similar estimate for the sample of x̄j = x̄ + aj.
The null hypothesis is now equivalent to
H0: aj = 0 for all j
Similarly, we can represent each element in the sample as xij = μ + αj + εij where εij denotes the error for the ith element in the jth group. As before we have the sample version xij = x̄ + aj + eij where eij is the counterpart to εij in the sample.
Also εij = xij – (μ + αj) = xij – μj and similarly, eij = xij – x̄j.
If all the groups are equal in size, say nj = m for all j, then
i.e. the mean of the group means is the total mean. Also
Click here for a proof of Property 3.
Observations
MSB is a measure of the variability of the group means around the total mean. MSW is a measure of the variability of each group around its mean, and, by Property 3, can be considered a measure of the total variability due to error. For this reason, we will sometimes replace MSW, SSW and dfW by MSE, SSE and dfE.
In fact,
![]()
![]() If the null hypothesis is true, then αj = 0, and so
If the null hypothesis is true, then αj = 0, and so
While if the alternative hypothesis is true, then αj ≠ 0, and so
If the null hypothesis is true then MSW and MSB are both measures of the same error and so we should expect F = MSB / MSW to be around 1. If the null hypothesis is false we expect that F > 1 since MSB will estimate the same quantity as MSW plus group effects.
In conclusion, if the null hypothesis is true, and so the population means μj for the k groups are equal, then any variability of the group means around the total mean is due to chance and can also be considered an error.
Thus the null hypothesis becomes equivalent to H0: σB = σW (or in the one-tail test, H0: σB ≤ σW). We can therefore use the F-test (see Two Sample Hypothesis Testing of Variances) to determine whether or not to reject the null hypothesis.
Relationship with F distribution
Property 4: If a sample is made as described in Definition 1, with the xij independently and normally distributed and with all μj equal and all equal, then
Proof: The result follows from Property 1 above and Property 1 of F Distribution.
Example resumed
Example 1 (continued): We now resume our analysis of Example 1 by calculating F and testing it as in Property 4.
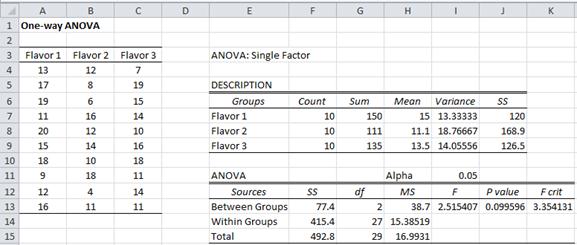
Figure 2 – ANOVA for Example 1
Based on the null hypothesis, the three group means are equal, and as we can see from Figure 2, the group variances are roughly the same. Thus we can apply Property 4. To calculate F we first calculate SSB and SSW. Per Definition 1, SSW is the sum of the group SSj (located in cells J7:J9). E.g. SS1 (in cell J7) can be calculated by the formula =DEVSQ(A4:A13). SSW (in cell F14) can therefore be calculated by the formula =SUM(J7:J9).
The formula =DEVSQ(A4:C13) can be used to calculate SST (in cell F15), and then per Property 2, SSB = SST – SSW = 492.8 – 415.4 = 77.4. By Definition 1, dfT = n – 1 = 30 – 1 = 29, dfB = k – 1 = 3 – 1 = 2 and dfW = n – k = 30 – 3 = 27. Each SS value can be divided by the corresponding df value to obtain the MS values in cells H13:H15. F = MSB / MSW = 38.7/15.4 = 2.5.
F test
We now test F as we did in Two Sample Hypothesis Testing of Variances, namely:
p-value = F.DIST.RT(F, dfB, dfW) = F.DIST.RT(2.5, 2, 27) = .099596 > .05 = α
Fcrit = F.INV.RT(α, dfB, dfW) = F.INV.RT(.05, 2, 27) = 3.35 > 2.5 = F
Either of these shows that we can’t reject the null hypothesis that all the means are equal.
As explained above, the null hypothesis can be expressed by H0: σB ≤ σW, and so the appropriate F test is a one-tail test, which is exactly what F.DIST.RT and F.INV.RT provide.
We can also calculate SSB as the square of the deviations of the group means where each group mean is weighted by its size. Since all the groups have the same size this can be expressed as =DEVSQ(H7:H9)*F7.
SSB can also be calculated as DEVSQ(G7:G9)/F7. This works as long as all the group means have the same size.
Data Analysis Tool
Excel Data Analysis Tool: Excel’s Anova: Single Factor data analysis tool can also be used to perform analysis of variance. We show the output for this tool in Example 2 below.
The Real Statistics Resource Pack also contains a similar data analysis tool that also provides additional information. We show how to use this tool in Example 1 of Confidence Interval for ANOVA.
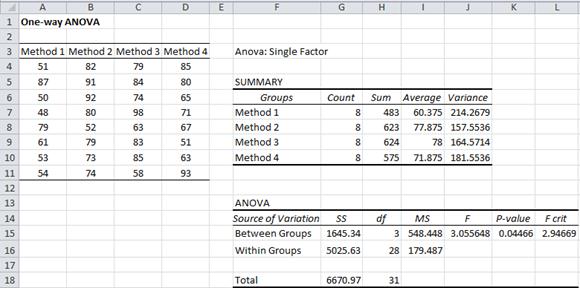
Example 2: A school district uses four different methods of teaching their students how to read and wants to find out if there is any significant difference between the reading scores achieved using the four methods. It creates a sample of 8 students for each of the four methods. The reading scores achieved by the participants in each group are as follows:
Figure 3 – Anova: Single Factor data analysis tool
This time the p-value = .04466 < .05 = α, and so we reject the null hypothesis, and conclude that there are significant differences between the methods (i.e. all four methods don’t have the same mean).
Note that although the variances are not the same, as we will see shortly, they are close enough to use ANOVA.
Observation: We next review some of the concepts described in Definition 2 using Example 2.
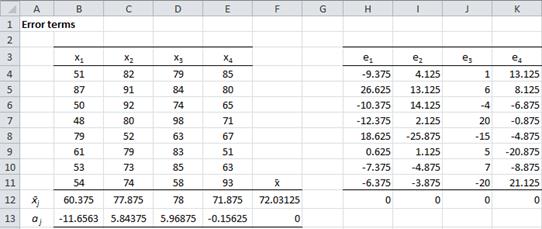
Figure 4 – Error terms for Example 2
From Figure 4, we see that
- x̄ = total mean = AVERAGE(B4:E11) = 72.03 (cell F12)
- mean of the group means = AVERAGE(B12:E12) = 72.03 = total mean
= 0 (cell F13)
= 0 for all j (cells H12 through K12)
We also observe that Var(e) = VAR(H4:K11) = 162.12, and so by Property 3,
which agrees with the value given in Figure 3.
Example with unequal groups sizes
In Examples 1 and 2, all the group sizes were equal. This doesn’t have to be the case, as we see from the following example.
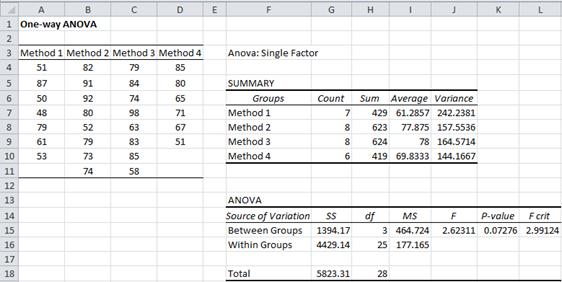
Example 3: Repeat the analysis for Example 2 where the last participant in group 1 and the last two participants in group 4 leave the study before their reading tests were recorded.
Figure 5 – Data and analysis for Example 3
Using Excel’s data analysis tool we see that p-value = .07276 > .05 = α, and so we cannot reject the null hypothesis and conclude there is no significant difference between the means of the four methods.
Generalizing t-test for two samples
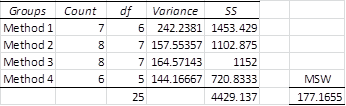
MSW can also be calculated as a generalized version of Property 1 of Two Sample t-Test with Equal Variances. There we had
When there are more than two groups, MSW can be calculated as a generalized version of the above formula
From Figure 6, we see that we obtain a value for MSW in Example 3 of 177.1655, which is the same value that we obtained in Figure 5.
Figure 6 – Alternative calculation of MSW
Calculating SS between groups
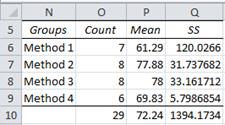
As we did in Example 1 we can calculate SSB as SSB = SST – SSW. We now show alternative ways of calculating SSB for Example 3.
Figure 7 – Alternative calculation of SSB
We first find the total mean (the value in cell P10 of Figure 7), which can be calculated either as =AVERAGE(A4:D11) from Figure 5 or =SUMPRODUCT(O6:O9,P6:P9)/O10 from Figure 7. We then calculate the square of the deviation of each group mean from the total mean. E.g. for group 1, this value (located in cell Q6) is given by =(P6-P10)^2. Finally, SSB can now be calculated as =SUMPRODUCT(O6:O9,Q6:Q9).
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack contains the following supplemental functions for the data in range R1:
| SSW(R1, b) = SSW | dfW(R1, b) = dfW | MSW(R1, b) = MSW |
| SSBet(R1, b) = SSB | dfBet(R1, b) = dfB | MSBet(R1, b) = MSB |
| SSTot(R1) = SST | dfTot(R1) = dfT | MSTot(R1) = MST |
| ANOVA(R1, b) = F = MSB / MSW | ATEST(R1, b) = p-value |
Here b is an optional argument. When b = True (default) then the columns denote the groups/treatments, while when b = False, the rows denote the groups/treatments. This argument is not relevant for SSTot, dfTot and MSTot (since the result is the same in either case).
These functions ignore any empty or non-numeric cells.
For example, for the data in Example 3, MSW(A4:D11) = 177.165 and ATEST(A4:D11) = 0.07276 (referring to Figure 5).
Real Statistics Analysis Tool
Real Statistics Data Analysis Tool: As mentioned above, the Real Statistics Resource Pack also contains the Single Factor Anova and Follow-up Tests data analysis tool which is illustrated in Examples 1 and 2 of Real Statistics Support for ANOVA.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
Zar. J. H. (2010) Biostatistical analysis 5th Ed. Pearson

Pls I did an analysis on one way anova but the way the probability section of the anova is not clear to me. For instance, one prob reads 7.023E-10. pls what does this mean how do I correct it?
Hello Gbenga,
This value is in scientific notation and means 7.023 times 10 to the minus 10th power. It is the same as 0.00000000007023. This is a very small number close to zero.
Charles
Hello Charles
How can I calculate the number of subjects in each group of three acute, chronic disease and control to start a Kinetic study?
regards,
Hello Saja,
You can physically count them. Alternatively you can use Excel’s COUNT or COUNTIF function. Exactly which function to use depends on how your data is formatted.
Charles
Hello Charles,
I have set of data to perform statistics, i have patients with different tribes and I have their food dietary info say for e.g meat,fist, etc 8 types of foods they consume and i have different time duration e.g nil, daily. weekly and monthly as how much they consume and does these food habit effects patient . so my question is what kind of test i can perform to know whether these food habits has any effect on the patients or not? could please guide ?
Thank you
Mary
Hi Mary,
If you have three factors (Tribe, Food, Time), then you can perform 3-way ANOVA. See
Factorial Anova
I don’t understand the part about time duration. If this is the amount of food that each subject consumes in each time period, then this is a repeated measures factor, and requires Repeated Measures ANOVA or Repeated Measures MANOVA. These are also covered in the Real Statistics website.
Finally, you need to define how you will measure the effect on the patients of these food habits. Is this cholesterol level, body-mass index, etc.?
Charles
Hello Charles,
Thank you.
the time duration 2 timesa day like wise weekly and monthly . no it is not cholesterol or body-mass, i would like to see the significance if any on patients having certain disease for example diabetes does food habit has effect on patient if they consumes certain at certain time may it be daily or weekly or monthly. and which food habit has more influence o the patients disease?
Thank you
Mary
Mary,
With all these variations, you probably want to use regression to model the various possible combinations.
Charles
Thank you charles,
I shall try to do it 🙂
Mary
Hello Charles,
I have done several tests (monocyte,leucocyte count, etc.) on 5 groups (negative control, positive control, low dose, medium dose, high dose) of 5. Which analysis is suitable for this kind of data?
Hello Abigail,
What hypothesis or hypotheses do you want to test?
Charles
I want to know whether the various tests for the different groups differ significantly.
Abigail,
It does appear that ANOVA is a suitable test. Which version of ANOVA will depend on information that you haven’t provided.
Charles
Hello Charles,
Please this is an example of the data:
TEST NEG. CONTROL POS. CONTROL LOW DOSE MEDIUM DOSE HIGH DOSE
RBCs 23 43 44 26 12
PLATELET 12 13 12 26 32
MONOCYTE 101 111 198 564 111
NEUTROPHILS 33 35 33 31 30
There are 5 data points for each group.
Hello Abigail,
I still need to understand your design, and so let me ask a few questions:
1. Do you have six groups (a negative control group, a positive control group, a treatment group, a low dose treatment group, a medium dose treatment group and a high dose treatment group)? If so, how many subjects are in each group? How do the positive and negative control groups differ?
2. Are there really six groups, including a treatment group or are there actually only 5 groups, including 2 control groups and 3 treatment groups?
If there are really six groups, what sort of dosage does the treatment group get?
3. You list 4 types of measurements: RBC, platelets, monocytes, neutrophils. Are these the only measurements that you are studying? Are you taking these measurements for each subject in each group after the study is done (i.e. there is only one of each of the four measurements for each subject in each group)?
4. What hypothesis or hypotheses are you trying to test?
Charles
i need the step using ms.excel
This is described in Example 2 on this webpage.
Charles
hello, i wanna ask. how to state the correct hyphotesis for testing equality of means in density for three materials using ANOVA? and the data that i have from the three materials are decimal value.
i need ur help. thanks.
Hello, this is described on this webpage, namely the null hypothesis is that “the density means for the three materials are equal” It is just that simple.
Charles
Hello,
I did a test comparing negative control, positive control, low dose, medium dose and high dose groups with n=5 for each group. Is the ANOVA a good method to determine significant difference between groups or a student’s t-test? What post hoc test is also appropriate in this case? What particular parameter am I to use to say that one group is significantly different from another?
Hello Abigail,
Assuming that you have 5 independent groups, ANOVA is a good way to go. There are a number of choices for post hoc test, depending on what hypotheses you want to test; it is likely that Tukey’s HSD is the correct choice, but this depends on a number of criteria. See the following webpages for more info:
Unplanned Comparisons
Planned Comparisons
I don’t understand your last question.
Charles
Hello Charles,
Thanks for your assistance. I meant to ask how you would know from the ANOVA whether the positive control group was significantly higher than the negative control group for instance.
Because when I used ANOVA, there was just one table containing the SS df MS F P-value F crit. It seems not enough to say one group is significantly different from the other. Is that where the post hoc tests come in? I’m using excel for my analysis so any test that I can use excel will be much appreciated. Thanks
Hi Abigail,
To get more detailed results, of the type that you are requesting, you need to perform follow up testing (also called post hoc tests). These are explained at
https://real-statistics.com/one-way-analysis-of-variance-anova/planned-comparisons/
https://real-statistics.com/one-way-analysis-of-variance-anova/unplanned-comparisons/
There are quite a few post-hoc tests to choose from. Usually Tukey’s HSD is a good choice, but the most appropriate choice depends on many factors, as explained on these webpages.
Charles
Thanks so much Charles. You’ve been a great help.
Dear Dr chales
I have 3 groups A,B and C each group with 10 samples
Bodyweight from each group taken for 0-70 days weekly base.
I want run one way ANOVA?
Hello Yusuf,
What do you mean by “each group taken for 0-70 weekly base”? Does this mean that you have measurements each of the 11 weeks (including 0)? Are these the 10 samples or are these in addition to the 10 samples per group?
Charles
Dear Charles
I am interested in analysing my trial data by one-way ANOVA with replications and repeated measures. The trial was simple: field plots were sprayed with 3 products x 3 rates plus one reference product and one control (11 treatments). There were 4 replicates of each treatment. Insect mortality was observed at 4 and 8 days after treatment. I would like to separate sample means, is Tukey’s HSD a reasonable method for this case? I can’t seem to find in the RealStats Add-in to Excel a way to analyze by one-way ANOVA with replications and repeated measures. Thank you.
Hi Charles,
Thanks for the excellent explanation of ANOVA. I think there’s one typo here. Under “Property 2” section, “Also εij = xij – (μ + αij) = xij – μj” should be “Also εij = xij – (μ + αj) = xij – μj and similarly”. Right?
And another question: Under “Property 3” section, you said “If the null hypothesis is true then MSW and MSB are both measures of the same error”.
Personally, I think if null hypothesis is true, MSB tends to be zero since the variance between sample means will be very small. However, MSW will always be bigger because null hypothesis being true or false doesn’t impact the variance within groups. Am I right?
Really appreciate it for your reply. Thanks again.
Hello Huan,
Yes, you are correct. aij should be aj. I have now corrected this on the webpage. Thanks for catching this typo.
Regarding MSW and MSB, I suggest that you perform ANOVA on the following data (or something similar where it is clear that the null hypothesis is likely to be true). You will see that MSW is bigger than MSB, MSB is not close to zero but it is close to MSW.
A B C
1 1 1
2 2 2
3 4 3
4 4 4
5 5 5
6 6 5
Charles
Ciao Charles,
Thanks for the reply.
As for the data array:
A B C
1 1 1
2 2 2
3 4 3
4 4 4
5 5 5
6 6 5
I calculate the result as follows:
MSB=0.16667
MSW=3.21111
, where MSB is close to zero rather than MSW.
Enlight me per favore. Grazie mille!
Ciao Huan,
When looking at the population value E[MSW] <= E[MSB] where equality occurs when the null hypothesis is true. I guess this is not evident from the sample values MSW and MSB. Charles
Hi Charles,
I am doing some analysis to determine whether financial ratios differ between business enterprises of different sizes. I have a large sample of data but there are outliers. Comparing just two enterprise sizes I used your trimmed means t test. As I want to create more enterprise sizes (eg large, medium, small, micro enterprises) I would need to do ANOVA. But what about the outliers?
Can I winsorize the data and carry out the ANOVA on the winsorized data?
Thank you for your assistance
Jack,
I don’t see any reason why you couldn’t perform Anova with trimmed or Winsorized data. Just keep in mind that the outcome will relate not to the original data, but to the trimmed or Winsorized data.
Charles
Hi Charles, using your given examples,how can i generate LSD value for each column? assuming each column is a different variable e.g Height, weight etc. how can i generate LSD value for the two variables ?
Charo,
I assume by LSD you mean least significant difference. I am not sure what you mean by finding LSD for each column since LSD refers to a comparison between two variables. Real Statistics doesn’t support LSD as a post-hoc test after a t test, but you might consider using Tukey HSD instead.
Charles
It’s amazing to pay a quick visit this website and reading
the views of all friends about this post, while I am also keen of getting knowledge.
Dear Dr. Charles,
I should perform a one-way ANOVA that is strongly unbalanced, because I have 3 groups with n1=104, n2=12 and n3=7 samples respectively.
Anyway, both normality and homogeneity of variances assumptions are satisfied.
The test resulted not significant with F = 0.675 << Fcrit = 3.07, but in your opinion, do you think that such a test is not meaningful by itself?
The data come from biometric measures of a given population, so there is no way to re-design the test to obtain a more balanced groups.
Thank you very much for any suggestion!
Best Regards
Piero
Piero,
The results should be valid, but I suggest that you create a box plot to make sure that the means look reasonably different. The big problem may be the statistical power of such a test, which is probably quite low.
Charles
Charles,
the means doesn’t look different. I computed the power of the test by following your formulas described in the section “Power for One-Way ANOVA”. In effect, the computed power is low (18.9%), but I didn’t understand very well if such formulas can be used also in a very unbalanced design.
Thank you very much
Best Regards
Piero
Piero,
The formulas can be used even in this case.
The two biggest drawback with such unbalanced models are:
1. Power tends to be based mostly on the smallest sample. This means that power will generally be quite low (as you have found)
2. The model is more sensitive to departures from the homogeneity of variances assumption
Charles
Charles,
many thanks for your help!
Piero
Is it possible to make “live anova table” using excel functions? And which functions have to be used?
I am running a laboratory and my data set changes continusly.
Perhaps the following webpage will help
https://real-statistics.com/one-way-analysis-of-variance-anova/confidence-interval-anova/
Charles
I have data regarding returns of six indsutries. I wish to know the inter industry and intra industry returns difference? will anova help?
Priti,
Quite possibly. It depends on the details.
Charles
Hi,
Is there a maximum of Degrees of Freedom that we can use?
I’m using Excel (Anova Single Factor) to calculate this:
I have monthly rolling returns data, and (there’s 1533 df of them), it gives me P-value of 0.01155 (thus I will reject the Ho at alpha=0.05),
but if I use yearly rolling returns data (meaning I just use January data of every year), I only have 126 df, and the P-value is 0.6610 (thus I do not reject the Ho at alpha = 0,05)
Does that means ANOVA test differs if I use too much data?
How to determine the best # of data to use?
Nathania,
The more data you have the more likely you are to get a significant result. This is because with a lot of data, even small differences can be detected (which might not be detected with a small amount of data). This is why it is important not just to focus on “significance”, but also on effect size. Just because you detect a significance difference, doesn’t mean that this difference is large. In fact, with a large sample even small differences (measured by effect size) can be significant, while large differences in a small sample might not be significant.
You shouldn’t worry about having too much data and so there isn’t a best amount of data to use, except from the point of view that it might be expensive or time-consuming to collect a lot of data. Also having too little data might mean that your test is not powerful enough (i.e. it is too susceptible to type II error).
Charles
Thank you for the information well illustrated ,
can i use ANOVA single test for robustness parameter for microbiology validation ?
Limson,
What is the robustness parameter for microbiology validation? What do you need to test about such a parameter?
Charles
Hi there, i want to ask which test should i use in pre-post test design, with 2 groups. I want to use a intervention and post that i want to see the difference between the experimental group and control group.
Can I use ANCOVA?
Kalpna,
It seems like a Repeated Measures ANOVA of the type described on the following webpage:
https://real-statistics.com/anova-repeated-measures/one-between-subjects-factor-and-one-within-subjects-factor/
Charles
I can easily grasp the concept of ANOVA if there are the same number of terms present in each column, I can even compute it in hand manually using a pen, paper, and calculator. But I cannot get do it anymore if the number of terms in every column is now different from the other columns of the same data.
Ariel,
The calculation for one-way Anova is the same even when the columns have different numbers of items (see Example 3 on the referenced webpage).
The situation is more complicated for two-way Anova where you do need to use a different approach (based on regression).
Charles
I get it if it is still one-way but no longer on two-way. I teach to students one-way and they like it more but a waste of time due to formulas needed to be done.
Uh, so it also means that one-way ANOVA is also applicable even if the number of items in each column are different from the other columns? I’ve read a local book here in the Philippines, and those formulas are for sum of squares (both between and within), due to that they have both summation symbols, n (the number of items in each column) will be represented as “n sub i”. I’ll use your Example 3 and I’ll try to solve it by hand.
Ariel,
Yes, you can use one-way ANOVA even when the number of elements in each column are different.
Charles
I need your help. I need the assumptions of the ANOVA
which tests to run and in what order to not violate the ANOVA function
Peggy,
See Assumptions for ANOVA
Charles
Hi, Charles .. brilliant work I must say.. By any chance do you have the datasets posted somewhere. Since I could not find any direct link to the datasets.
Chunky,
See Examples Workbooks
Charles
Dear Charles,
I have 3 groups of income, low, middle and high income.
Then I have data about purchased luxurious goods of each group.
I conducted ANOVA and I got the result that there’s a different among populations’ means. Then what statistical test I should use to point out that the lower income people get, the less they purchase luxurious goods.
Judy,
You have a number of choices, including Tukey HSD and contrasts.
These described on the Planned and Unplanned Comparisons webpages.
Charles
Which type of statistical tests I should use in order to prove the relationship between variables? (Example: Students who have higher GPA tend to have higher monthly salary)
Thank you!
Judy,
This really depends on the type of data you have. You might use a t test or Mann-Whitney or ANOVA, etc.
Charles
I have a sample of 1400. One column is GPA score, one column is corresponding salary after graduation. My assignment require me to see whether people with higher GPA in school will have better salary? I want to use ANOVA, but I think I can only draw a conclusion that they’re related but cannot point out a positive connection between them.
Thank you for your reply,
Judy
Judy,
You can use the correlation coefficient or linear regression.
Charles
So if the coefficient is positive so I can conclude the relationship, can I using t-test
Judy,
Sorry, but I don’t understand your question.
Charles
please, can you help me run my analysis? on groundwater
You will need to provide some additional information.
Charles
Dear Charles,
Thank you very much for devoting time to prepare such a detailed material.
This is the only material I found that combines three fundamental things: The theory behind the process, the formulas to calculate step by step and the analysis tools shortcut.
I found only one minor mistake when applying your example:
You wrote: “dfW = n – k = 30 – 2 = 28”
I think it should be: dfW = n – k = 30 – 3 = 27
Again, thank you for your effort.
Dear Wagner,
Thank you for your very gracious comments about the materials.
Thank you also for catching this error. I have now corrected the webpage as you have suggested. Thanks to you and contributions from people like you, the site gets better and more accurate every day.
Charles
If the value of F is greater than F crit, does it mean we reject the null hypothesis? or accept?
Samantha,
If F > Fcrit, then you reject the null hypothesis. This is a right tailed test.
Charles
Nice class. Loved the examples and clarified the basic very well. I loved the factors. One can say the MS(b) as the signal of variance and MS(w) as the noise of variance and the F stat is a ratio of singal / noice.
Thanks for this post
Hello Charles,
Thank you for your insightful lesson on ANOVA.
I am trying to a find a test that determines if the the within variance of two groups is greater than or less that the between variance.
I tried using the coefficient of variance but I found that the within and between values did not differ by much.
I would like to know if I can use ANOVA or Kruskal-Wallis to evaluate within and between differences in the variance of two groups. I noticed that ANOVA gives the within variance of each group but it does not give me the between variance. If not, can you refer me to another test that can evaluate group variances.
Thank you in advance for your assistance.
Regards,
Katrina
Katrina,
I am not sure why you would want to do this and I can’t think of a way of doing this analysis.
You can test whether two variances are equal using the approach shown on the webpage:
https://real-statistics.com/chi-square-and-f-distributions/two-sample-hypothesis-testing-comparing-variances/
This approach probably doesn’t apply since the two variances that you are interested in are not coming from independent samples.
Charles
Charles,
I would like to evaluate the variability of pollution within and between cities.
As such the data will be from independent samples.
I looked at the F-distribution but it only gives me information about the variation within a data set.
However I was hoping to evaluate if the variability between the cities is greater than within.
Katrina
Charles,
Please forget about my last writing on the expectations of MS(Between) and MS(Within). Sorry for the time you lost on trying to understand. I should have waited before sending it.
I have nevertheless two comments on the text Basic Concepts for ANOVA.
1. In Observation, just before Property 1: the text should be, I think,
“MS(within) is the sum of the group variances weighted with the factor [n(j) – 1] /SUM[n(j) – 1]”
2. In Property 3: text should be
“E[MS(Between)] : sigma(E)^2 + SUM[n(j)*a(j)^2]/df(B)”
Thanks again,
Erik
Erik,
1. Yes, you are correct. I have now changed the text accordingly. Thanks for your help.
2. I don’t really understand this.
Charles
Hi Charles!
This article is very helpful. Thank you.
To clarify, how big of a difference is acceptable when dealing with unbalanced sample sizes? I am looking at four trials where equipment was running at different speeds. Speed 1 has ~340 data points, speed 2 has ~130 data points, and speed 3 and 4 have ~50 data points. The variances are close and the data is normally distributed, but are these differences large enough to preclude the use of ANOVA? If they are, is there a different method available in the Data Analysis tool pak in Excel to analyze my data?
Thanks again!
Anna,
I don’t know of any unacceptable difference in data sizes when the normality and homogeneity of variances assumption is violated. I would use ANOVA. The power of the test will tend to be reduced (based on a sample size more towards the lower sample size).
Charles
Charles,
I am somewhat puzzled by the statement E[MSw] = SigmaSq epsilon.
Knowing that:
E[MSw] = SigmaSq w and
Var(e) = (n-k)/(n-1) *MSw and
E[Var(e)] = SigmaSq e
So:
E[Var(e)] = SigmaSq e = (n-k)/(n-1) *SigmaSq w and now
E[MSw] = (n-1)/(n-k) *SigmaSq e
If this were true the constant in the second term of E[MSb] would also change.
I realise of course that the logic of the F-test remains untouched.
Where is the flaw in my reasoning?
Thank you again,
Erik
Erik,
Perhaps I am missing something obvious, but I am not following your logic.
Charles
Good day
I am very pleased to see an organisation that seeks to help students and researcher .You are the only source of comfort the student in my school ENS have found now. I am an undergraduate student in Cameroon . please i hope you will be of help to me, we have been taught ancova, anova etc . Please just brief me I will do the rest, It goes like this , read the following passage and answer the question that follows
A school district has 24 secondary school, and each school has only one 9 grade classes for information technology learner.the class size of the school is composed of 35 to 40 students. conduct a survey study using 50% of the information technology students in every school in each school.
1) which sample technique is the most appropriate to use
2)Explane why you considered the sample technique you have chosen above
THANKS
Yves,
Sorry, but I don’t like to answer school assignments. I am happy to give insight and answer questions that help you better use statistics, but I believe that you should do school assignments and not me.
Charles
Hi! Thanks for this Charles! This really helped. However, I still have to test significant difference on densities between two locations , each having 3 different groups. Can you help me? Hoping to hear from you. Thank you!
Christen,
This may be a two factor ANOVA, but you need to provide more information before I can help you.
Charles
Please, thxns for idea of helping students, i am an undergraduate student and very new in the field of reseach . please can u help me through more light to the following questions
Q1— which is the best approarch in comparing test of significants use to comparing respective post test means scoresof an experiment and control group made from thesame experimental group and explane why you choose the either ANCOVA, ANOVA and T-test,
Q2—Why is it important to determine the validity of the data instrument and which is the intended form of validity used when determining the monthly measure for a course
Prince,
These look like questions asked in your course in the context of the lessons you have received. Since I don’t have this context (since I didn’t attend your course), I really can’t answer your questions. I can suggest that for Q1, you look at the following webpages for more information about tests following ANOVA:
Planned Comparisons
Unplanned Comparisons
Charles
Thanks for your reply please. this question is doesn’t have any context for which is based on , I have recurrently made this question amongst pass questions as i am and have been facing difficulties in creating a context to answer the question that is why I solicited your advice. Thanks
Sorry, but I don’t have anything to add to my previous response.
Charles
Really good! I have one question, you people may find simple to answer. What should be the maximum value/level/cutoff of within group variance to conduct an ANOVA or depends on ANOVA result? I dont mind whether mean are differing significantly or not. I know there are many tests to know suitability of data to perform an ANOVA, but its does not satisfy my need. I want know, what should be maximum within group variance to understand that sampling was correct. since many a time high withing group varince reduce the F-ratio and make group mean difference insiginficant, despite of high variation between group.
I don’t know of any maximum group variance assumption. The main thing is that group variance be similar.
Charles
Excellent material. I recommend the next didactic video respect ANOVA https://www.youtube.com/watch?v=-yQb_ZJnFXw of the professor David Longstreet
Sorry, I meant By calculating the target amount of *analyte weighed
Dear Sir,
I am a stats novice and need help addressing establishing control limits with multiple lab data. I am attempting to generate control limits using data from our 3 regional labs. I asked each lab to utilize 3 analysts for N=6 replicate testing.
Analyst mean-target mean comparison – I’d first attempted to check the individual analyst data. By calculating the target amount of analyst weighed in the sample to be tested and applying a standard deviation to come up with a target range I required that all means observed fall within the range.
Analyst-to-Analyst mean comparison – Next, I would attempt to compare the analysts means within each lab before combining them. I’d use One-Way ANOVA to determine if there was a significant difference in the means. If there is no significant difference I’d combine the 3 analyst data and calculate the overall lab mean. If there is a significant difference I would perform a Two-Sample t-Test lab 1 and 2, then 1 and 3, then 2 and 3 to try to see which mean pairs had significant difference. This would be done for each lab.
Lab-to-Lab mean comparison – For the means the same approach used in the analyst-to-analyst comparison above is applied to determine if there was a significant difference in the lab means. If there is no significant difference I’d combine the 3 labs data and calculate the overall population mean.
Finally, After the population mean is generated I’d then use the SW test on the new population to conclude with 95% confidence that the data are normally distributed. From there I calculate the UCL, CL and LCL of my control chart.
Q: Is the One-Way ANOVA the correct test to apply to the analyst-to-analyst and lab-to-lab comparisons?
Q: For the means comparisons that show significant difference is the Two-Sample t-Test the correct test to apply to the mean pairs? Would this be enough to zero in on the problem mean or is there more to do?
Q: Once the good data from the analysts within their lab, then the good data from all labs have been combined is the SW test correct for determining normal distribution about the new population mean?
Q: Finally, if the SW test shows the population to not have normal distribution should I use a series of Grubb’s tests to call out outliers or another test?
Keith,
Here are brief answers to your questions
Q: Is the One-Way ANOVA the correct test to apply to the analyst-to-analyst and lab-to-lab comparisons?
A: There is also the possibility of interactions between the two factors. For this reason, you might be better off running a two factor ANOVA.
Q: For the means comparisons that show significant difference is the Two-Sample t-Test the correct test to apply to the mean pairs? Would this be enough to zero in on the problem mean or is there more to do?
A: Once again, the approach you described ignores any interactions. This may not be desirable.
Q: Once the good data from the analysts within their lab, then the good data from all labs have been combined is the SW test correct for determining normal distribution about the new population mean?
A: The SW test is used to determine whether the population is normally distributed (not the population mean). For most purposes this is the test I would recommend to check for normality. I would also graph the sample data to see whether it looks to be normally distributed (e.g. using a QQ plot).
Q: Finally, if the SW test shows the population to not have normal distribution should I use a series of Grubb’s tests to call out outliers or another test?
A: You should try to identify outliers whether or not the population is normally distributed. Grubbs’ test is one way to do this. Other approaches are described on the website. Even if the data is not normally distributed, most tests (t tests and ANOVA) are fairly robust to violations of normality, but if the data is very skewed or quite clearly not normal, then you should seek to use other methods. These include transformations of the data, Mann-Whitney test or Wilcoxon signed-ranks (instead of t test), Kruskal-Wallis or Welch’s ANOVA (instead of ANOVA), etc.
All of these approaches are described on the Real Statistics website.
Charles
Thanks for the enlightenment sir. Very much so appreciated!
Hi Charles,
Your page is very helpful! I needed help with a question.
For a runs test with large sample size a Z value is calculated but for smaller sizes a separate table is used. Why is this the case? (5 Marks)
Thanks
Raj,
For large samples, the statistic used is approximately normally distributed, but this may not be the case for small samples, and so a table which is different from the critical values for the standard normal distribution is used. This sort of thing is true for quite a few tests.
Charles
thank you for this lesson. It is helpful for me.
can you help me to find what is meaning of leading beverage?
thanks and regard..
Here I mean a leading beverage brand (e.g. Coca Cola or Perrier).
Charles
Dear Charles
Thank you for the excellent resource and explanations. I have a question that might sound more philosophical to many. When you said above “ANOVA can be a reasonable choice if the non-normality is not too severe (esp. if the data is relatively symmetric). Also ANOVA can be used if the homogeneity of variance assumption is not strongly violated.”
How do you measure “not too severe” or “not strongly” ? i.e. how do I know that my data is within “acceptable” limits in violating the rules ? The use of very or too is a bit confusing
Many Thanks
It turns out that Statistics is not just “science” but also “art”. You can perform tests for normality, symmetry and homogeneity of variance (e.g. Levene’s test), but at the end there is also judgement.
Charles
Thanks Charles.
There is a question I am confused. Five groups of raw data do not meet either the the normality assumption or homogeneity of variance test (their p value are all equal zero). However, the sample sizes are equal, with each group containing 5000 samples. Under this situation, an ANOVA test is OK?
Thanks a lot!
If the assumptions for ANOVA are not met, esp. if the variance are very different, then you should probably not use ANOVA. The likely best approach is Welch’s test.
Charles
Assumption is that each population will have same mean and same variance in ANOVA.
Ria,
What is this in relationship to?
Charles
I tried to copy the data of the example and paste them transposed, then I set b = False in atest.
I get different results, could you help me?
Ruggero,
I also don’t get the same answer. It looks like an error. I will fix this in the next release of the software, which I plan to distribute in the next two or three days. Thank you very much for identifying this mistake.
Charles
Dear Charles!
I thank you very much for an information you furnished to researchers about different statistical tools. I wanna ask you one question concerning to significance test. Which statistical too is widely used to test the significance of growth of branches, employees, asset etc of 4 commercial banks over a period of 10 years? Branches, employees, asset etc are parameter used to measure the growth and development of a bank. I did it (i.e., I have computed the growth rate of each bank using each parameter) but still I didn’t get the way to test the significance of each parameters for each bank. So would you help me? T-test is used to test the mean of two variables? What about for single variable? Is a single factor ANOVA analysis is appropriate?
Sorry, but you haven’t supplied enough information for me to be able to answer your question.
Charles
Dear Charles;
I need to assume my null hypothesis is differences between means. i mean is there any way or trick or test to switch alternative hypothesis with null hypothesis? as i find out, all of these tests are based on reaching the result that the means are not equal. i need to show the means are equal at the end.
thanks
Since the null and alternative hypotheses are complements of each other, it doesn’t seem necessary to use any tricks. Just use the usual tests. Rejecting the null hypothesis gives evidence for the alternative hypothesis and retaining the null hypothesis gives evidence against the alternative hypothesis. If you are concerned about the significance level, just change the value of alpha.
Charles
Hi, this is a stupid question but I am just wondering, why we called in Analysis of variance where in fact we analyzed the mean instead???? should it be ANOM, analysis of MEAN?
This is a very reasonable question. ANOVA tests whether group means are statistically equal, but the way it does this is by changing the problem into an equivalent one about variances (i.e. the MS). The F test essentially tests whether two characterizations of the variance are equal.
Charles
Send the procedure for computing ANCOVA manually and the use of SPSS
Sorry, but I don’t understand your comment.
Charles
thank you very much for this valuable information.
please send me about the use of CV, t-grouping, tuky’s HSD and Fisher’s LSD
There is info on the website about the first three. I don’t support Fisher’s LSD. E.g. you can find info about Tukey’s HSD at https://real-statistics.com/one-way-analysis-of-variance-anova/unplanned-comparisons/
Charles
Dear Charles,
First of all I wanted to thank you for this really helpful website and resource pack!
As a practice example I used Ex#2 of Basic concepts for ANOVA to perform, Shapiro-Wilk-Test, Levene-Test, and ANOVA. When I do the Shapiro-Wilk-Test on each of the groups I find that groups/methods 2-4 follow a normal distribution but group/method 1 does not. I thought in the case of a non-normal distribution I wasn’t allowed to perform ANOVA. I’m not very advanced in statistics, so I would really appreciate your help.
Many thanks!
You are perfectly correct. Anova assumes that each of the groups follows a normal distribution, although it is fairly forgiving about this assumption. Shapiro-Wilk and a QQ Plot show that Method 1 does not meet the normality assumption (although the sample size is so small that any conclusion either way is quite tenuous), and so Anova shoud not be used.
In fact the non-parametric Kruskal-Wallis Test (which does not assume normality) shows that the null hypothesis that the group medians are equal should not be rejected (whereas the Anova test shows that the null hypothesis that the means are equal should be rejected).
I used this example since it is simple to understand. I will shortly be updating the Anova portion of the website and I will either flag the problem that you have identified or change the example.
Thanks for bringing this issue up.
Charles
Dear Charles,
Thank you so much for your detailed answer!
I have one more question with this type of analysis that I couldn’t find the answer to:
If the result of the Shapiro-Wilk-Test is that one of my groups doesn’t meet the normality assumption, I have to do the Kruskal-Wallis Test instead of ANOVA. If the result of the Levene’s Test is that there’s no homogeneity of variances, I have to do Welch’s Test instead of ANOVA.
Is that correct?
Which test (instead of ANOVA) do I have to do if Shapiro-Wilk and Levene’s Test say that I don’t have a normal distribution and I don’t have homogeneity of variances?
Are you planning on including Welch’s Test in the Resource Pack anytime soon?
Thank you again so much for this great website and your help!
ANOVA can be a reasonable choice if the non-normality is not too severe (esp. if the data is relatively symmetric). Also ANOVA can be used if the homogeneity of variance assumption is not strongly violated. If the sample sizes are unequal (unbalanced models) then violation of homogeneity of variance can be a problem.
My understanding is that Krusal-Wallis and Welch’s are both acceptable if the data is not normal and/or the homogeneity of variances is violated. For most such situation it seems that Welch’s procedure generally gives better results than K-W, except where the normality assumption is more than moderately violated. There are also versions of Welch’s involving trimmed/Winsorized means/variances which might give better results in such situations.
I hope to add Welch’s procedure in the next release of the Real Statistics Resource Pack (Rel 3.2). If it doesn’t make it in that release I will certainly include it in the following release.
I came across the following article which may be useful in trying to decide which test to use.
http://home.cc.umanitoba.ca/~kesel/Cribbie_param_bootstrap_feb_2010.pdf
Charles
Thank you so much for these detailed explanations. This was very helpful! I’m reading the paper you suggested right now. Thanks for including the link, very kind.
This website is really the most helpful resource I found on the internet regarding both the stats explanations and the resource pack to perform analyses!