We explain how to calculate the effect size, power, and minimum sample size required for McNemar’s test. We will use the notation found in McNemar’s Test.
Effect size
We will use ψ = max(A/B, B/A) as a measure of the effect size. For Example 1 of McNemar’s Test, the effect size is 11/6.
We can view the null hypothesis of the test as ψ = 1.
Statistical Power
You can estimate the power of McNemar’s Test for an effect size of ψ as NORM.S.DIST(zβ, TRUE) where
n is the sample size, p = min (A/n, B/n) based on a pilot study or some historical information, and zα = NORM.S.INV(1-α/2) for a two-tailed test and zα = NORM.S.INV(1-α) for a one-tailed test.
Sample Size
Solving for the above formula for n provides an estimate of the minimum sample size required to detect an effect of size ψ at the required power.
Examples
Example 1: Suppose that Example 1 of McNemar’s Test describes the results of a pilot study. What is the power of a study based on a sample of size 500 to detect an effect size of at least 2? I.e. what is the probability of rejecting the null hypothesis in this case?
First, we observe that p = min(6/100, 11/100) = .06. Note that if we want to take the continuity correction into account, we would use p = min((6+1)/(100+1), (11-1)/(100+1)) = 7/101 = .0693. Since we use a two-tailed test, NORM.S.INV(1-.05/2) = 1.95996, and
Thus, the power of the test is NORM.S.DIST(1.2452, TRUE) = 88.7725.
Example 2: What does the sample size need to be to achieve power of 95% for the study in Example 1?
In this case, NORM.S.INV(.95) = 1.644854, and
Thus, a sample of size at least 644 is required.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2012) McNemar’s test
https://en.wikipedia.org/wiki/McNemar%27s_test
Zar. J. H. (2010) Biostatistical analysis 5th Ed. Pearson
NCSS (2024) Tests for two correlated proportions (McNemar test)
http://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/PASS/Tests_for_Two_Correlated_Proportions-McNemar_Test.pdf
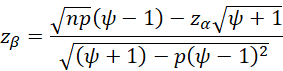
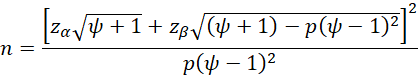
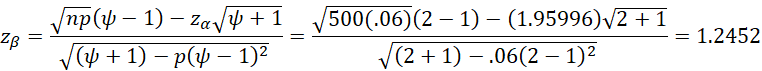

Hi! I am wondering if you have any sources that link to what would be considered a small, large, or medium effect size using the calculations you provided from Zar’s textbook?
I believe that Cohen’s original papers on this subject provide measures for small. medium, and large effect sizes.
Keep in mind that these are guidelines only.
Charles
Greetings from Singapore Dr Charles.
I stumbled upon your page whilst seeking a method to derive sample size for matched-paired sample proportions. As a preliminary point, I thank you for free resources. It has been an invaluable asset to the wider internet community.
I write to you to seek your guidance regarding your sample size formula above. You stated that “p = min (A/n, B/n)”. However, in NCSS documentation for “Tests for Two Correlated Proportions (McNemar Test)” with the same formula for sample size, it stated that p = A/n + B/n (expressed as “PD = P10 + P01” in document).
Could you perhaps clarify which is the correct version for the variable p and why? If both versions are valid, could you perhaps share when one should use one over the other?
The link to the NCSS documentation is produced below for your perusal,
http://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/PASS/Tests_for_Two_Correlated_Proportions-McNemar_Test.pdf
You will find the sample size formula in page 3 of the documentation.
I look forward to your reply.
Best regards,
Yat-Hon
Hi Yat-Hon
Glad that you stumbled across Real Statistics.
The procedure described on the Real Statistics website comes from Zar’s textbook (reference given on the webpage). This book in turn uses the procedure
CONNETT. J. E., J. A. SMITH. and R. B. McHUGH. 1987. Sample size and power for pair-matched case-control studies. Statist. Med. 6: 53-59.
I don’t know why the formulas are the same as in the NCSS description except for the definition of the p term. Have you tried to use both approaches to see how different the sample size estimates are?
Charles