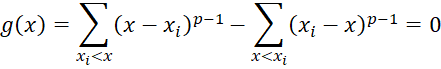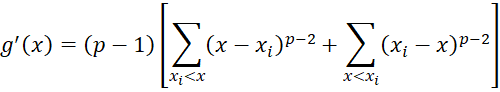We can obtain the value of the Lp estimates of central tendency described in Lp Estimators by using Newton’s method. Care must be taken since the function ||X–x||p is not differentiable at x = Lp(X).
Our goal is to find the value of x that minimizes ||X–x||p. It is sufficient to minimize the function
This occurs when
which is equivalent to
The derivative of g(x) is
for p ≠ 1.
Thus by Newton’s method, we iterate until convergence to find the value x = x(k) where
![]()
References
Zornoza, J. (2020) Distance metric for machine learning. Aigents
https://aigents.co/data-science-blog/publication/distance-metrics-for-machine-learning
Wikipedia (2020) Minkowski distance
https://en.wikipedia.org/wiki/Minkowski_distance