Objective
Note that the coefficients in Figure 1 of Trend Analysis (and the TREND_COEFF worksheet function) are valid only when the treatment groups are equally spaced. We now show how to derive the linear and quadratic coefficients for unequally spaced treatments. The approach for polynomial degrees > 2 is more complicated and so we won’t discuss these further here.
Methodology
Shortly, we will revisit Example 1 of Trend Analysis, except that this time the dosages (shown in row 1 of Figure 1) are 5, 10, 12, 15, 20. These are not evenly spaced. We now show how to calculate the linear and quadratic coefficients when this is the case.
Linear coefficients
Step 1: find the mean of the dosages
Step 2: subtract the mean from each of the dosages
Step 3: if possible, multiply the values from step 2 by some number (which can be a fraction) so that the resulting values are integers without a common divisor.
Figure 1 – Linear coefficients
The mean of the dosages in range A1:E1 is 12.4 (cell H1), as calculated by =AVERAGE(A1:E1). This value is subtracted from each of the dosages as shown in range A2:E2. This is done by placing the formula =A1-$H1 in cell A2, highlighting range A2:E2, and pressing Ctrl-R. We next want to get rid of the fractional part of these values. We can do this by multiplying each value by 5, as shown in row 3. Note that we could have multiplied each value by 10, but in that case, the resulting values would have a common divisor of 2.
Quadratic coefficients
Step 1: Calculate the sum of the squares Q of the linear coefficients
Step 2: Calculate the cum of the cubes C of the linear coefficients
Step 3: Set u = –C/Q and v = –Q/k where k = the number of treatment groups
Step 4: For each linear coefficient c, the corresponding quadratic coefficient is c2 +uc + v
Step 5: If possible, try to multiply the coefficients from step 4 by a number so that all the resulting values are integers without a common divisor.
Figure 2 – Quadratic coefficients
Range J2:N2 contains the linear coefficients. Cell P2 is calculated by the formula =SUMSQ(J2:N2), cell Q2 by the array formula =SUM(J2:N2^3). Cell R2 contains =-Q2/P2 and cell S2 contains =-P2/COUNT(J2:N2). We now calculate the quadratic coefficients by placing the formula =J2^2+$R2*J2+$S2 in cell J3, highlighting range J3:N3, and pressing Ctrl-R. There is no point in using step 5 in this case.
Example
Example 1: Repeat Example 1 with the same data values, except that the dosages are now 5, 10, 12, 15, and 20.
We can now perform the trend analysis in a manner similar to that shown in Figure 4 of Trend Analysis, using the new linear and quadratic coefficients, accepting that we can’t test for cubic or quartic trends. We show this analysis in Figure 3.
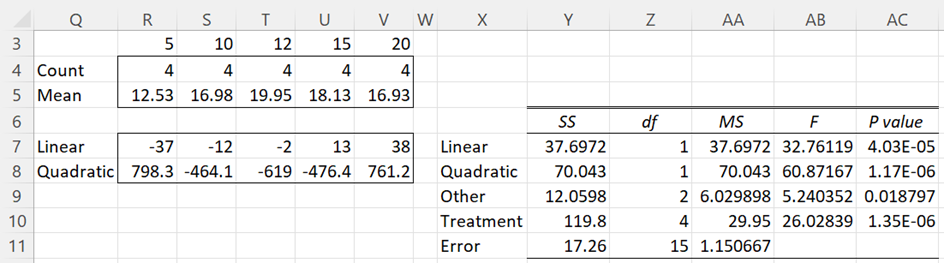
Figure 1 – Trend analysis with unequal intervals
Since we don’t have cubic or quartic coefficients, instead we create an “Other” line in row 9. Cells Y9 and Z9 contain the formulas =Y10-SUM(Y7:Y8) and =Z10-SUM(Z7:Z8). The MS, F, and p-value are calculated in the usual way. We were hoping that the p-value was not significant, but unfortunately, since p-value = .018797, we lost some information by not being able to include the cubic and/or quartic trends.
Note that if we had performed a similar analysis for Example 1 of Trend Analysis, we would have found that the p-value for Other was .102053, a non-significant result, as expected.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Bergerud, W. (1988) Determining polynomial contrast coefficients. Biometrics Information
No longer available online
Penn State (2024) Quantitative predictors: orthogonal polynomials
https://online.stat.psu.edu/stat502/lesson/10/10.2