Objective
When the assumption of equal population variances is not met for the Two-Sample t-Test with Equal Variances (or when you don’t have enough evidence to know whether it holds) you should consider using a modified version of the t-test. This version is based on the following property.
Key Property
Property 1: Let x̄ and ȳ be the sample means and sx and sy be the sample standard deviations of two samples of size nx and ny respectively. If x and y are normally distributed, or nx and ny are sufficiently large for the Central Limit Theorem to hold, then the random variable
has a t distribution T(df) where the degrees of freedom is expressed as
The nearest integer to df is sometimes used.
An alternative version (Satterthwaite’s correction) of df (which has the same value) is calculated as follows
Welch’s t-Test
Property 1 can be used to test the difference between sample means even when the population variances are unknown and unequal. The resulting test is called Welch’s t-test. The degrees of freedom for this test will be smaller than (nx – 1) + (ny – 1), the degrees of freedom for the t-test where the variances are equal.
When nx = ny then the value of t in Property 1 is the same as in Property 1 of Two-Sample t-Test with Equal Variances. If, in addition, the variances are equal, then the df values are also the same, which means the p-values of the two tests are the same.
Worksheet Functions
Real Statistics Function: The Real Statistics Resource Pack provides the following function.
DF_POOLED(R1, R2) = degrees of freedom for the two-sample t-test with unequal variances for samples in ranges R1 and R2 (i.e. df in Property 1).
Excel Function: Excel provides the function T.TEST to handle the various two-sample t-tests.
T.TEST(R1, R2, tails, type) = the p-value of the t-test for the difference between the population means based on samples R1 and R2, where tails = 1 (one-tailed) or 2 (two-tailed) and type takes one of the following values:
- the samples have paired values from the same population
- the samples are from populations with the same variance
- the samples are from populations with different variances
These three types correspond to the Excel data analysis tools
- t-Test: Paired Two Sample for Mean
- t-Test: Two-Sample Assuming Equal Variance
- t-Test: Two-Sample Assuming Unequal Variance
Note that when type = 3 the T.TEST function uses the value of the degrees of freedom specified in Property 1 unrounded, while the associated Excel data analysis tool rounds this value down to the nearest integer. On this webpage, we explain how T.TEST is used when type = 2 or 3, while we describe the version where type = 1 in Paired Sample t Test.
The T.TEST function is not available in versions of Excel prior to Excel 2010. For these versions of Excel, the equivalent TTEST function is used instead.
The T.TEST and TTEST functions ignore all empty and non-numeric cells. Both tests assume that α = .05.
Example
Example 1: In Example 1 of Two-Sample t-Test with Equal Variances, we assumed that the population variances were equal since the sample variances were quite similar. We now repeat the analysis assuming that the variances are not necessarily equal.
We use the Excel formula T.TEST(A4:A14,B4:B14,2,3). The first two parameters represent the data for each sample (without labels). The 3rd parameter indicates that we desire a two-tailed test. Finally, the 4th parameter indicates that we are employing a t-test with two independent samples from populations whose variances are not assumed to be equal. Since
T.TEST(A4:A14,B4:B14,2,3) = 0.042642 < .05 = α
we reject the null hypothesis. Note that if we use type = 2, i.e. T.TEST(A4:A14,B4:B14, 2, 2) = 0.040219, the result won’t be very different, which is consistent with the fact that the sample variances are similar (and presumably so are the population variances).
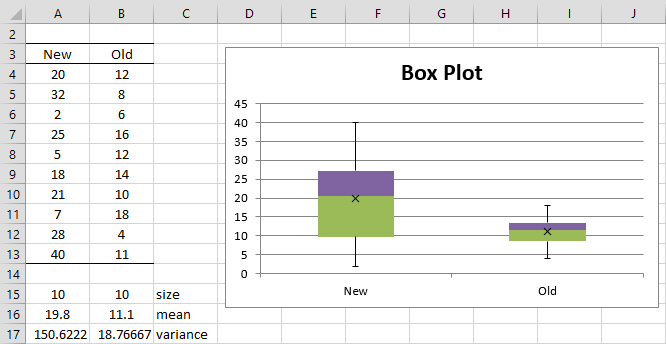
Example 2: Repeat the analysis for Example 1 but with different data for the new flavoring as shown in Figure 1.
Figure 1 – Sample data and box plots for Example 2
Clearly, the sample variances are quite unequal. Using the T.TEST function with type = 3 we get
T.TEST(A4:A13 ,B4:B13, 2, 3) = 0.05773 > .05 = α
and so this time we cannot reject the null hypothesis (for the two-tailed test). Note that if we had used the test with equal variances, namely T.TEST(A4:A13, B4:B13, 2, 2) = 0.048747 < .05 = α, then we would have incorrectly rejected the null hypothesis.
Data Analysis Tools
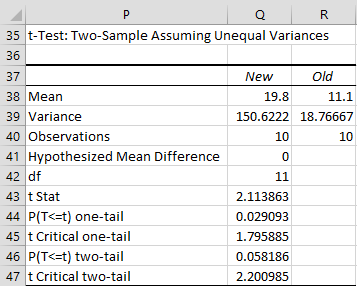
We can also use Excel’s t-Test: Two-Sample Assuming Unequal Variances data analysis tool for Example 2. From Figure 2, we see that the results are the same.
Figure 2 – Data analysis for the data from Figure 1
Note that the p-value returned by T.TEST is slightly different from that reported by the data analysis tool. This is because the data analysis tool rounds the df to the nearest integer while T.TEST does not.
We can also use a Real Statistics data analysis tool to conduct this test or other versions of the t-test. Click here for details and examples.
Equal Variances Assumption
Generally, even if one variance is up to 3 or 4 times the other, the equal variance assumption will give good results, especially if the sample sizes are equal or almost equal. This rule of thumb is clearly violated in Example 2, and so we need to use the t-test with unequal population variances.
If the variances are equal then the equal and unequal variances versions of the t-test will yield similar results (even when the sample sizes are unequal), although the equal variances version will have slightly better statistical power.
Effect Size
The calculation of the effect size and the effect size confidence interval is the same as for the case where the two samples have equal variances. If the variances are very different, then it might be better to use the variance of one of the samples (e.g. the one representing the Control group) instead of the pooled variance. This version of Cohen’s d effect size is called Glass’ delta.
Cohen’s d* and Hedges’ g*
Another approach is to use Cohen’s d* which is defined by
where
We can now define the less biased Hedges’ version of this effect size, namely
where m = df*/2 and
Example
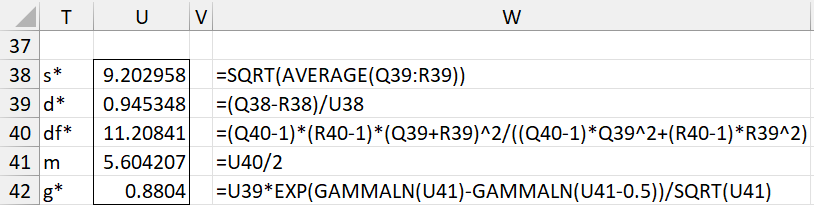
We can calculate d* and g* for Example 2 using the data in Figure 2 as shown in Figure 3.
Figure 3 – Cohen’s d* and Hedges’ g*
Interpretation
The default interpretation of Cohen’s d* effect size is
- .20: small effect
- .50: medium effect
- .80: large effect
Confidence Intervals
Click here for a description of how to estimate confidence intervals for Cohen’s d* and Hedges’ g*.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
Microsoft Support (2022) T.TEST function
https://support.microsoft.com/en-us/office/t-test-function-d4e08ec3-c545-485f-962e-276f7cbed055
Delacre, M., Lakens, D., Ley, C., Liu, L., Leys, C. (2021) Why Hedges’ g*s based on the non-pooled standard deviation should be reported with Welch’s t-test
https://psyarxiv.com/tu6mp/download
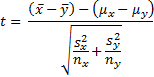
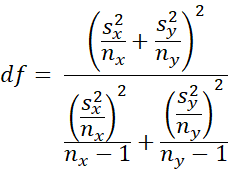
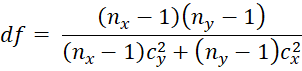
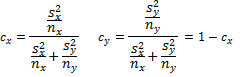
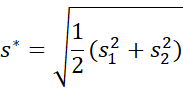
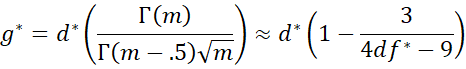
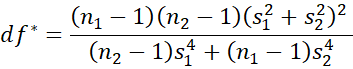
Hi Sir,
Will you help me interpret my data in t-Test: Two-Sample Assuming Unequal Variances
t-Test: Two-Sample Assuming Unequal Variances
Lethrinus nebulosus Siganus Sutor
Mean 0.244083333 0.351354167
Variance 0.015854884 0.028630815
Observations 24 24
Hypothesized Mean Difference 0
df 42
t Stat -2.491592797
P(T<=t) one-tail 0.008375702
t Critical one-tail 1.681952358
P(T<=t) two-tail 0.016751403
t Critical two-tail 2.018081679
Thank you
Davina,
Assuming that the normality assumption is met (or not severely violated), p = .01675 indicates a significant result, i.e. Siganus Sutor is significantly larger than Lethrinus nebulosus.
Charles
Hi Sir,
Can you please interpret the above data using F test please as I’m getting confused when it comes to using the Statistical tables to solve it if the sample sizes were the same.
Elizabeth,
I don’t know what F test you are referring to. If it is to determine whether the variances are equal, then please see the following webpage:
https://real-statistics.com/chi-square-and-f-distributions/two-sample-hypothesis-testing-comparing-variances/
Charles
Hi Charles,
I need to test statitstics difference of two means. Both samples are related to one factor (e.g. net sales), however, each subject in one sample can experience same value several times and they are unequal samples. So can you please advice which test I should use?
Thank you for your help!
Nhi,
Are you saying that some subjects are measured multiple times (yielding potentially different measurements)?
Charles
Hi Charles,
I’m not sure. I will explain clearly. For example, we have 2 sample with net sales data. Sample 1 includes firms with characteristic 1, sample 2 consists of firms with characteristic 2. Example of sample 1 as follows.
Obs Firm Year Net sales
1 Firm A 1 1,000
2 Firm B 1 1,200
3 Firm A 1 1,000
4 Firm A 2 1,500
5 Firm B 1 1,200
6 Firm B 2 2,000
7 Firm A 1 1,000
8 Firm C 1 3,000
9 Firm B 2 2,000
Similar to sample 2. But 2 samples are unequal.I need to test difference in two means of net sales.
Thank you for your help.
Nhi.
Nhi,
The fact that the samples are unequal in size is not a problem. The problem is that certain firms have multiple measurements (e.g. A and B). We could use repeated measures ANOVA based on year, but again I see multiple measurements. In this case, though, the multiple measurements are all identical, and so it looks like your data is really only:
1 Firm A 1 1,000 (also sample 3, 7)
4 Firm A 2 1,500
2 Firm B 1 1,200 (also sample 5)
6 Firm B 2 2,000 (also sample 9)
8 Firm C 1 3,000
Now the only problems are: (1) Firm C is missing data for year 2 and (2) you don’t have much data.
Charles
Hi Charles,
Thank you for your answer. It’s just an example, not real my data. I need test means between two sample across firm and year. You mean that I should use repeated measures ANOVA. However, I think that test looks like just for indicator number (0,1) not for continuous data. So do you think can I delete mutiple measures and remain only 1 observation for 1 firm in 1 year? I mean for above example, there is remaining only 5 observations.
Nhi.
Nhi Nguyen,
It really depends on what hypotheses you want to test. You can also take the average for a year when you have multiple years. Again it depends on what you are trying to discover.
Charles
what is E in p two tail
Shane,
If you are talking about a number like 7.2E-03, this means 7.2 x 10^(-3) = .0072
Charles
how to determine the significance level .05 in test statistic using unequal variance i have 50 and 100 observation…
Shane,
.05 is the traditional number used for the significance level in almost all circumstances.
Charles
Hi, Can you explain the computational formula Excel uses for the two sample mean t-test for samples with unequal variances. I’ve attached the Microsoft web address which shows the equations used but little else. In particular what are the delta sub o, m and n variables?? Thanks …Andy
https://support.office.com/en-US/article/Use-the-Analysis-ToolPak-to-perform-complex-data-analysis-6c67ccf0-f4a9-487c-8dec-bdb5a2cefab6?CorrelationId=75a256ba-fb01-463e-873d-4f8e41714752&ocmsassetID=HA102748996
Andy,
I explain this topic on the following webpage:
https://real-statistics.com/students-t-distribution/two-sample-t-test-uequal-variances/
Charles
Hi,
Supposing we get a p-value greater than alpha for a one tailed t test, can we look at the tstat and tcritical to compare the two arrays ?
If yes, how do we do that ?
Giridhar,
Sorry, but I don’t understand your question. You can test using the p-value or the critical value. The conclusion will be the same.
Charles
Hey, would I be able to use T-test unequal variances with my data? By comparing issues in medication (Grouping them in main headings) and using the outcome (resolved by “A”), so e.g. Grp 1 med v Grp 2 med and outcome resolved by “A” (being 1) and resolved by “other” (being 0). My data size also ranges from 1 to 53, (I’m also thinking of excluding some data size from <6) would it be possible to use T-test unequal variances or another test would be more appropriate.
Hello, I am currently doing a project in class based off of a survey our class created. Our professor told us to all form our own hypothesis based on the data. I am having trouble creating my hypothesis and figuring out which test to perform. I really want to compare female vs. male coping mechanisms given social media. Would it be inappropriate to hypothesize that Females tend to have more appropriate coping mechanisms more so than males when it comes to social media? Also would I just use an unpaired t-test?
Courtney,
You have not provided enough information to determine what is the appropriate hypothesis, but what you have proposed at least sounds plausible. Two sample t test could be appropriate.
Charles
So say I had a t Test : Two Sample Asumming Equal Variances
Variable 1 Variable 2
Mean 4.0875 8
Variance 5.267857143 18.28571429
Obs 8 8
pooled variance 11.77678571
Hypo mean differ 0
df 14
t stat -1.81237697
P(T<=t) one tail 0.045002328
t critical one tail 1.761310136
P(T<= t) two tailed 0.090004655
t Critcal two tail 2.144786688
how would I explain this in everyday language?
Assuming that you are performing a two-tailed test, the fact that p-value = .09 > .05 = alpha, indicates that there is is no statistical evidence for rejecting the null hypothesis that the samples come from populations with equal means.
Two cautions though:
1. The variances are not equal and so you should probably use the t test assuming unequal variances. I don’t expect the test to be that much different, but you should check this out.
2. The calculation of the t stat doesn’t seem correct. t = the difference between the means divided by the pooled standard deviation times the square root of the sum of the reciprocals of the sample sizes. Thus t = (4-8) / (sqrt(11.78)*sqrt(1/8+1/8)) = -2.33.
Charles
Hi,
I conducted a lab to try to reject the null hypothesis: “The rate of cellular respiration/oxygen consumption of a pea (plant) is the same as cricket (animal).”
Would the t-test be appropriate?:
Minutes Cricket Pea
0
3
6 0.015 0
9 0.035 0.04
12 0.045 0.045
So this 1st trial’s t-test results was .85 > .5 meaning that the difference between the rates of cellular respiration in the pea and cricket are not significant, thus we failed to reject the null, correct? And if so, when is a t-test appropriate? I referred to the link below:
http://projects.ecfs.org/prepole/BIOLOGY%2013-14/Labs/Cell%20Respiration%20Lab/Analyzing%20Respiration%20Data%20using%20T-test%202014.htm
Vivian,
It sounds like the t test could be appropriate, but I don’t know how you calculated the value of .85 or where the .5 came from.
By the way, how many peas and crickets were sampled and which version of the t test did you use?
Charles
I have selected return of a particular stock to know impact of stock split. I have taken return 3months before and after. I want to use t test. I also want to test that after return is higher than before or not. Same I want use it with other variable i.e turnover. Please guide me in this regard.
Satarupa,
This is described on the referenced webpage. Do you have a specific question?
Charles
My question is by using paired two sample mean ttest, if p value is less than .05 (accept H1), Can I infer return before split is lower than after split.
Yes, generally that is the conclusion that you would reach.
Charles
Thank you so much Sir. This website is really helpful.
Which t test formulae will I use to test my hypothesis if the population is 79 and 101..
Hypothesis: there is no significant difference in mean score between male and female teachers in regards to capacity building
Sorry, but I don’t understand what you mean by the population is 79 and 101.
Charles
Hi Sir,
Will you help me interpret my data in t-Test: Two-Sample Assuming Unequal Variances
t-Test: Two-Sample Assuming Unequal Variances
Generic Branded
Mean 2.079 2.126
Variance 0.070 0.024
Observations 11 11
Hypothesized Mean Difference 0
df 16
t Stat -0.512
P(T<=t) one-tail 0.308
t Critical one-tail 1.746
P(T<=t) two-tail 0.616
t Critical two-tail 2.120
Maireen,
Assuming a significance level of alpha = .05, the fact that the p-value > alpha indicates that you can’t reject the null hypothesis that the samples come from population with equal means.
Charles
In the example, the T.Test (type 3) function and the Real Statistics tool both return a two-tailed p of 0.05773 — but Excel’s data analysis tool returns 0.0582. What accounts for this slight discrepancy? Thanks!
The T.Test function uses the exact value for the degrees of freedom, while Excel’s data analysis tool (and the T.DIST function) rounds the degrees of freedom down to an integer value.
Charles
Ah yes, thanks!
Thanks for the great article! I do have one follow up question however. I am still unclear as to which test to use based on the number observations.
To give an example, I am looking to compare two columns of data; column A holds performance data before a change was made and column B holds performance data after a change was made. Both columns are for the same individual. The null hypothesis would be that there is no change in performance after the change is made. Column A has 30 observed values (n=30) and column B has 12 observed values (n=12). Is the data in column A and B still paired meaning I would use the two sample t-test for equal variances or is it unpaired due to the difference in n values meaning it would be a two sample t-test for unequal variances?
Thanks for your time, I look forward to hearing from you!
-J
John,
To use a paired test, (1) the sizes of the two groups must be the same, (2) each element in A must be independent of the other elements in column A (in particular, they can’t be from the same subject) and each pair of elements in the same row must be from the same individual.
Charles
Hi sir,
I am to determine if factors affecting employee turnover are the same as factors affecting employee retention. I have a frequency distribution table stating how many respondents consider each factor relevant to retention and turnover. So my data arrays are frequency counts for each factor. Array 1 for retention and Array 2 for turnover for the same factor. Example
Pay 28% 14%
Met expectations 16% 12%
Trainings 8% 4%
How do I apply the t-test to this analysis?
Thanks
I’m conducting a test to determine if there is a quality difference between diaper brands. Unfortunately, my sample size is 12. 7 particpants for size 3 and 5 participants for size 4. My original plan was to conduct a t-Test: Paired Two Sample for means test (Ho: mu BENCHMARK BRAND – mu PROPOSED BRAND = 0, HA: mu BENCHMARK BRAND – mu PROPOSED BRAND 0) at the 5% level of significance. However, after I run the test in excel, my two tail P-Value is higher than I’d like. Therefore, this is leading me to think I should use two sample t-Test: unequal variances. Regardless, my question is, with a small sample size which statistics test mentioned above is ideal for comparing two samples? Or do you need more info to answer?
Ben,
Irrespective of the outcome, you can’t use the paired t test when the samples are independent. You need to use the independent t test. You are correct that you shouldn’t expect too much with such small samples (unless the sample means are quite different). You can check the power of the test as described on the Power of the t test.
Charles
Hi
I have two fungal organism one is wild type (parent strain) and the other is mutant type of the same strain. I would like to compare between gene expression in the two organisms. Which type of t-test should be used to know if the gene expression is significant or not?
Tanks
Moustafa,
I would need to know more details, but it sounds likely that you need a two sample t test.
Charles
Hi,
This was a very helpful article.
I have the experimental data on temperatures from 2 sets of experiments that involve heating up of liquids under specific conditions. One set of data is for water where I did 5 experiments and have recorded the final temperature values. Other set of data is for salt water (brine) where I did 6 experiments and have recorded the final temperature values. I would like to compare the results of water and brine. From chemical data, the final temperatures of brine is expected to be lower than that of water. So I know that I would like to do a one-sided t-test.
However, I am new to statistical methods and was wondering how I can use excel to do such a test. Should my ‘Variable 1 Range’ in Excel data analysis be water or brine or does it matter for an one sided test? Because, I want make sure that I am checking for the case that brine temperatures are lower than water and not checking for the reverse scenario. Thanks a lot for your help.
Vijay,
It shouldn’t matter which variable you list first. You will get the same result in either case. In fact you will see both the 1 tailed and 2 tailed results.
When you say that you have done 6 experiments, do you mean 6 repetitions of the same experiment or 6 different experiments?
Charles
Hi,
I have two distinct samples-ESG performance of South African companies and ESG performance of Mauritian comapnies. I run a t test to establish if both are distinct from each other and I can reject the null hypothesis. However, if I want to know whether the performance from one sample (i.e. South Africa) affects the ESG performance of the other sample (Mauritian companies), what should I do? I would be grateful for any assistance.
Thank you!
Maria
Maria,
Putting statistics to the side, please give me an example (or examples) of how ESG performance in South African companies can be affect the performance of Mauritian companies.
Charles
Hi Charles. Thank you for responding. Essentially, using organizational theory, in particular institutional theory, we say that companies that operate in close proximity to each other tend to conform to certain established norms of behavior. In some cases, businesses may follow practices done by larger and more established firms which is what we tend to call mimetic pressure. So the grounds for forming the hypothesis that since companies in South Africa are in many ways more established than Mauritian companies, then it follows that Mauritian companies could imitate their practices (in my case ESG reporting). Hope that makes sense.
Maria,
Thanks for your clarification.
Regarding your original question, first we need to decide on how to measure “whether the performance from one sample affects the performance of the other sample”. It is easy to measure “correlation”, but it is more difficult to measure “causation” or “influence”. I don’t really know how you can measure this.
Charles
Charles,
Thank you very much. Yes, I have carried out correlation but I see perhaps I may need to look beyond statistical testing and carry out interviews with regulators of accounting information or specific case studies in these countries. But thank you so much for your help.
Hello.
I had my students run an experiment over 15 days where they measure the growth (budding) of lemna plants under different colors of light using white as a control. They then graphed the raw data (5 trials of each color), then got the slope of the linear trendline as the rate. I want them to compare each rate of growth to white using a t-test.
my expectation was each graph would have the 5 trials for that color (so 5 lines = 5 rates). Then they were basically comparing av rate for red to av rate for white using a t-test, then av rate for blue to av rate to white, etc. They were t-testing just the 5 averages to the other 5 averages. My question is for degrees of freedom. Would it be 5-2=3, or would they need to use all of the data points (so 15 days x 5 trials = 75 -2 = 73DF)?
Also, when excel does the t-test it calc the p value so does it already take DF into account?
Where as if they used an online calculator, they’d need to calc DF because they’d be given the t-calc, correct?
thanks so muc!
Bri,
If I understand the problem correctly, you are comparing averages of one color vs white over the 15 days. If so, I would use df = 5+5-2 = 8 if this is an independent samples test (5 plants getting white light vs 5 different plants getting red light) and df = 5-1 = 4 if this is a paired samples test (5 plants getting white light and separately getting red light.
You could instead use ANOVA on the averages taking all 5 colors into account. You could also use repeated measures ANOVA instead of taking averages. Finally you could use ANOVA with a fixed factor for color and repeated measures factor for time.
When Excel does the t test on the raw data (via T.TEST or TTEST) it calculates the df inside the software. When it uses the T.DIST, TDIST and other distribution functions, the user needs to supply the value for the df.
Charles
hi there,
I have sampled 2 different habitats to determine whether tree species vary between the 2 sites. To do a ttest am i putting the raw data in or the mean, variance worked out frm each habitat.?
Thank you
You should generally conduct the t test on the raw data and not the mean/variance. Without knowing more about the specifics of your scenario I can’t say much more.
Charles
Hi Charles!
I am completing research analysis in regards to the effect of different variables on the level of mental illness stigma. I am testing how one’s age affects the level of negative stigma, as well as how one’s previous exposure to mental illness affects the level of negative stigma.
I am at the point in my analysis where there was no significant correlation between age and level of stigma, so my professor suggested dividing the ages into two groups (a younger group and an older group) and performing a t-test on the stigma results in order to see if there is any relationship there. So I have done that in Excel, I have selected the stigma results from each age group and compared them in a t-test two sample unequal variance test. My question is: in the results, the only thing I can see that is relevant to a p-value for significance is listed as:
P(T<=t) one-tail 0.284053007
t Critical one-tail 1.71088208
P(T<=t) two-tail 0.568106014
t Critical two-tail 2.063898562
I know normally a p-value is a lower case p, so are those upper case P's not a p-value? If not, what am I doing wrong in order to find the statistical significance of my findings? Also, how do I decide whether or not I want a one-tail or two-tail value (as they are very different)?
Thank you!
Cait
Dear Cait,
The uppercase P is indeed the p-value. Generally, you should use the two-tailed t test. In this case, both the one and two tailed tests yield a result which is not significant. See Null Hypothesis for more details about the number of tails.
Charles
Hi, I am new to statistics so would like some help please
If I have a balance intervention which all participants underwent, and would like to establish and analyse whether the right leg or left leg was more effective at improving in balance, am I correct in using a t-test for independent samples.
Also how do I assume equal or unequal variance. All of the figures are different and varying therefore do I use unequal variance. I would like to use excel to analyse my data.
Many thanks.
Leonie,
Assuming that you are comparing each person’s right leg with his/her left leg, you should use a paired t test. This is because the right and left legs are not independent (since they belong to the same person).
Charle
Suppose I comparing two data sets, x1 and x2. The sample mean of x1 is larger that the sample mean of x2, their variances are different, and my hypothesis is mean(x1)>mean(x2). If I got it right, T.TEST(x1;x2;1;3) gives the probability of mean(x1)>mean(x2). Then, why T.TEST(x2;x1;1;3) gives the same result? I would spect T.TEST(x2;x1;1;3) to be smaller than T.TEST(x1;x2;1;3).
Thank your for your help, and for this useful tool and explanations.
Soledad,
This function doesn’t return the probability that mean(x1)>mean(x2). It returns the p-value of test, which is different. In fact, if you flip the x1 and x2 values, the result for the test remains the same. See Null and Alternative Hypothesis for more details about how to interpet a p-value
Charles
Hi Charles if the formula for Equal Variances is T= (xbar1 – xbar2) – (mu1 – mu2)/ SQRT (1/n1+1/n2), then what would be the formula if it were unequal variances?
Alex,
The formula is the first formula on the referenced webapage.
Charles
Sir, using the two sample t-test(welch) to compare the mean of two samples…how do I work out the standard deviation for both. Thanks.
The standard deviation for data in range R1 is calculated by STDEV.S(R1).
The standard error for the two sample t-test (Welch) is the denominator of the first formula in Theorem 1 of the referenced website.
Charles
Hi Charles
Iam not good with the statistic stuff but I found out that Ecel has a t-test equation and I got some results for me data and calculate t-test. However I don’t know how to interpret the t-test result, so what it mean, Would you please help me with that
Fofo,
The t test tests whether the means of two populations are equal based on a samples from each population. Also loom at the following webpage for more information:
Two Sample t Test
Charles
Hi Charles,
With unequal variances, which degree of freedom is reported in the text describing the results ? The adjusted Welch df or the “natural” df (n1+n2-2) ?
Example : (t(df?)=2.78; p=0,004)
Can’t find an answer on this on the web or in textbooks…
Thanx in advance for considering this,
Eric
Hi Eric,
As explained on the referenced webpage, the adjusted Welch df is reported.
Charles
Charles,
Thank you so much for the quick reply and your kindness.
Kudos for your website,
Eric
Hi Charles,
great and very helpful website!
I just have a small question: I calculated the total bacterial numbers in the blood of 20 boys at three different time points i.e., at age 1 yr, 3 yr and 5 yr. I am confused which type of t-test should I use to calculate the statistical difference between the different time points?
Many thanks in advance.
Ravi
Hi Ravi,
The t test can only be used with pairs and not triplets. Thus you would have to perform up to three paired t tests: 1 yr – 3 yr, 1 yr – 5 yr, 3 yr – 5 yr. With three tests, there is more chance for experimentwise error, and so if you usually use alpha = .05, you would have to reduce the value of alpha say to .05/3 = .0667.
The usual approach in this case, is to start by using a different test, namely Repeated Measures ANOVA. This will test whether there is a significant difference between all three times. If there is, then there are follow up tests to pinpoint where the differences lie.
I suggest that you look at the ANOVA and Repeated Measures ANOVA part of the website.
Charles
Dear Charles,
Thank you so much for your quick response. I got your point!
By the way, if I wish to compare the data of cell numbers only between two time points i.e., 1yr and 5 yr, which type of excel t-test shall then be appropriate?
Many thanks once again.
Ravi
Ravi,
In that case a paired t test is a good choice, assuming that each sample is at least reasonably symmetric.
Charles
Dear Charles,
Thank you so much for your advices.
Ravi
Hello sir Charles!
I am one of those people who gets their brains crumpled like hell when it comes to statistics.
I just want to know if waht t test should I use to know if there is a significant difference between my experimental values and a fixed theoretical value.
for example, exptl values are 1, 2, 3 and my theoretical values are 2, 2, 2
Hello Serna,
If the theoretical values are all 2, then you would use the one sample t test with hypothetical mean of 2. See the webpage
One Sample t Test
Charles
How would I write up the results of a Two-Sample Assuming Unequal Variances with the results with the mean (variable 1 -3.11; variable 2 – 3.04), variance 0.022 & 0.029,
observations 159 & 332, df 351, t Stat 4.53, P(T<=t) two-tail 8.15
I need to know how to write this information up in a detailed format.
I have not checked to see whether the t stat and df you calculated are correct, but T.DIST.2T(4.53,351) = 8.10E-06 and not the p-value you report (the E-06 part is important).
When you report your results, you need to relate the statistical results to the real-world problem you were studying. I will suppose, for illustrative purposes, that you are testing whether a particular training course is effective in reducing accidents. I will also suppose that the p-value is 8.10E-06, and so you have a significant result.
Using APA-like guidelines you would say something along the following lines:
On average participants achieved better test scores after the training course (M = -3.11, SE = 0.15, N = 159) than those who did not take the training course (M = -3.04, SE = 0.17, N = 332). The difference is significant t(351) = 4.53, p < .001 (two-tailed); this represents a xx-sized effect of d = xx. Note that I used the standard error instead of the variance. You should also report the effect size Charles
The variables are positive numbers. Would I use variance instead of standard error?
Thank you.
That the variables are positive numbers is not relevant, You can certainly use the variance, but generally the standard error is reported.
Charles
I am comparing three types of breathing during the shooting performance, but i have no the same number of people in each groups. So the situation seems like this:
A:1, 2, 3, 4, 5, 6, 7, 8, 9
B:1, 2, 3, 4, 5, 6, 7
C: 1, 2, 3, 4
Is it possible to evaluete it by t-test? What is the method???
Andrea,
You don’t need to equal sample sizes to use the t test. But you are comparing more than 3 samples and so you need to use one-way Anova instead of the t test. See the following webpage: One-way ANOVA.
Charles
Hi Guys,
I am doing research involving 65 samples at two different cycles, and seeing the impact these cycles (A & B) would have on the samples. Which t-test would be best to use and why?
Cardre,
You haven’t provided enough information for me to respond. What do you mean by cycles?
Charles
if you have more than 30 samples you should not be using the t-test. Use the normal gaussian curve to calculate the information you need.
Hi,
I have 2 questions:
1-why would I get 2 different T values when I run ttests in excel and spss?
2- I have a student who did a pre and post test but did not match up the ID number so correctly, what kind of ttest can she use, I am assuming can not used paired? Thanks
Jaclyn,
1. You should get the same values. If you send me an Excel file with your data and results I will try to see what has happened.
2. The student will need to match up the ID numbers to be able to run any type of analysis.
Charles
Hi,
I have a problem with my research. My lecturer told me to use both equal & unequal t-test but I don’t understand what the difference equal & unequal t-test.
My research was about the efficiency between conventional and islamic banks from 2008 to 2015.the efficiency was measure by four (4) financial ratio.
1) return on asset between conventional & islamic bank
2) net profit margin between conventional & islamic bank
3) debt ratio between conventional & islamic bank.
4) earning per share between conventional & islamic bank.
It is logic to use both equal & unequal to run the data in excel & how?
Hi,
In this situation, equal and unequal refers to variances of the two samples (actually the population, but the samples serve as surrogate for the population). You can calculate both versions (equal and unequal variances) of the t test using either Excel’s data analysis tools or the Real Statistics data analysis tools. For more information, see the referenced webpage or the following webpage for more information about the equal variances version of the t test.
https://real-statistics.com/students-t-distribution/two-sample-t-test-equal-variances/
The t test is used to determine whether there is a significant difference in the means between two samples. This sounds like a reasonable test to use for the problems you have listed.
Charles
Hello, I’m doing a t-test on part of a set of data using excel
1 mean is 1.6 with SD of 0.79, the other has a mean of 6.6 and a SD of 1.34. i’ve done the t test, selecting the first mean and SD as ‘array 1’ and the second lot as ‘array 2’. it’s a two-tailed test with unequal variance. I’ve got a p value of 0.48, which seems very high. have i done it correctly?
No, the arrays should contain the raw data, not the mean and standard deviation. You can perform the t test using TDIST or T.DIST using the means and standard deviations.
Charles
Hello. Is this suitable if I have 10 respondents, which will be taking medication and be observed for their blood pressure for 10 days, to know if the medication is significant? or should I do one t-test for each of the respondent? Not really sure.
Sorry for the bad english.
Unfortunately, I don’t understand your question.
Charles
I guess, you want to study the effect of “medication” on “blood pressure” of patients (Is this medication significantly contributing for curing Blood pressure?). There might be two approaches:
1. You need to collect data from two group of BP – patients, namely treatment (Those who are taking medication) and control group (without medication). For keeping the effects of any other factor minimal, trails should be randomized.
2. Collect data measuring blood pressure of patients before and after taking medication. Again, keeping the effects of any other factor minimal, trails should be randomized.
So, finally you will have data of BP of two different groups. You can apply t-test. I believe for first case; you can apply independent sample t-test (with unequal variance) and for second case you can apply paired t-test.
If Professor approves the approach.
I think it’s actually a within-subjects t-test, comparing pre-treatment BP with post-. I think you want to calculate the mean and SD of the BP for your 10 participants before they started the medication, and again after. Then you would compare those.
SIR.i am wondering could i compare t-test,welch and also mann whitney in term of mean.
as i am referring the journal article “should i use nonparametric method on two apparently non normal distribution”
some ppl said that this is no logic…however ,i do found some books to claim that under additional assumptions , mann whitney has the same distributons but shift of location occur,therefore we can use it to compare their means.
Generally, if you can satisfy the assumptions for the t test, you should use the t test; otherwise provided the shapes of the two distribution are similar you should use Mann-Whitney. The loss in power of using Mann-Whitney is pretty small even when the assumptions for the t test are satisfied, and so when in doubt you might as well use Mann-Whitney.
Charles
Good Afternoon
I am trying to justify that the current method of sample taking is not representative. I have data from an online analyser that analyses the material/ore as it is produced. We then take a few grab samples for laboratory for analysis. I am not sure, but I think the two sample t-test would be the best fit for me. FYI I have done the F-test for the two samples and the null hypothesis that the variances for the two samples that are equal were not satisfied. I know want to perform the t-test to show that the sample means are not same, thus justifying that the grab samples is not sufficient and we need continuous online samplers. Am I on the right track? Please help
If I am understanding correctly, you want to use the t-test for independent samples with unequal variances to test whether the two samples come from populations with the same mean. This seems like a reasonable approach to determine whether the grab samples are sufficient. Since you have already found a significant difference in the variances, you already have evidence that the grab samples are not sufficient.
Charles
Hi Charles, Thank you sooo so much for replying. To put some more clarity. I have more 40 000 data points that I have from an online analyser. This comes from one days production. Then I have a grab sample of 50 rocks (ore particles) that I re-analysed. I basically put it over the analyser 5 times so have 250 datapoints. If this sample was representative I assume that when plotting cumulative histograms of the two distribution (40 000 and 250 datapoints) should lay more or less on the same graph. Visually this is not the case. With my limited knowledge of inferential statistics the t-test with unequal variances seems to be the best option in comparing the two populations. Is this correct, since the population sizes are different. Is there another way that I can proof that the sample is not representative in a “fancy” way. Kind Regards
The t test is fancy enough. You can use the t test with unequal samples.
One caution: the 5 times that you have put each sample through the analyzer means that the sample of 250 datapoints are not independent, one of the assumptions for the t test. You might better averaging the 5 values for each rock to arrive at 50 data points, which you would compare with the 40,000 data points. Another, more complicated approach is to perform ANOVA with repeated measures.
Charles
Can you post the Unequal variance with a simpler examples?
Please explain more precisely what you are looking for since the example I gave is pretty simple.
Charles
hi sir,
I’m doing 2 independent samples mean t-test with unequal variances to verify the comparison in the performance of the GDP Growth between 2 countries (Jordan & Morocco).. I’m not sure of which sign to use in Null Hypothesis and also in Alternative Hypothesis.. Is it = & ≠ or ≤ & > or ≥ & < ?
It depends on whether you want to conduct a one-tail or a two-tail test. See Null and Alternative Hypothesis for more details.
Charles
Hello, I am not sure what T-Test to use for one of my experiments. I am measuring if there is a significant difference in the abundance of a species in two different habitats.
Niklas,
This seems like a good fit for a t test, but it depends on the nature of your data.
Charles
Hi Charles,
I noticed the formula for the two sample, independent t-statistic calculates the absolute value [=(ABS(H5-H6-J3))/G16] . Other software packages I have used do not use the absolute value and thus can produce negative t-statistics. Is this something I am misunderstanding?
Thanks
dawn
Dawn,
The sign is not particularly important since it depends only on which of the means is subtracted from the other. The p-value is identical. I used the absolute value since Excel’s two tailed formula — TDIST(t,df,2) or TDIST.2T(t,df) — requires a positive value for t.
Charles
Hello Charles,
I would like to know whether I am using the right t test for my data.I have two data set of male life span with mean-31.15 and 19.05,variances -287.1 and 217.6,N1=79,N2=78.I am using two sample assuming equal variances.The other data set is the number of eggs laid having mean-36.59 and 15.1, variances-1130.399 and 238.32,N1=41,N2=10.For this data set, I am using two sample t test assuming equal variances .Which p value I should consider for my result -one tail or two tail. Am I using correct statistical analysis or not if not please suggest what I should use.
Tripti.
If you goal is to determine whether the two populations have the same mean, then the two sample t test assuming equal variances seems like a good choice provided the assumptions for the test are met (principally that the data is not highly skewed).
For the second example, I suggest that you use two sample t test assuming unequal variances.
Charles
May I ask what the formula for the df (degree of freedom)? I noticed that the value for the df is also different when I use t-test with unequal variances and equal variances.
thanks!
Tanya,
The degrees of freedom for the unequal variances case is m in Theorem 1 on the referenced webpage.
Charles
t-Test: Two-Sample Assuming Unequal Variances
CONTROLLED GROUP ——— – EXPERIMENTAL GROUP
Mean 0.205416667 —————- – 0.184527932
Variance 0.000385934——————- 0.000686411
Observations 20———————————- 19
Hypothesized Mean Difference——————– 0
df —33
t Stat— 2.805852172
P(T<=t) one-tail– 0.004176129
t Critical one-tail– 1.692360258
P(T<=t) two-tail –0.008352257
t Critical two-tail– 2.034515287
Jam,
Assuming that alpha = .05, since p-value (two-tailed) = 0.00835 < .05 = alpha, you reject that hypothesis that the two populations (from which the samples came) have the same mean. Charles
can you please help me in doing my research study i don’t know how to solve the P-value. using T-test..
thank you! 🙂
You can calculate and interpret the p-value of the t test as described on the referenced page.
Charles
I want to know, i have samples from the same source. I have used two different methods to analyse them. I am trying to compare two different methods used to analyse the samples.
1. Can I use paired t-test?
2. Are the samples dependent or independent?
3. what do I do if the null hypothesis is rejected when t-calculated is greater than t-critical but p-value is greater than 0.05?
4. tell me which method to use.
thank you
1. It depends on what you mean by the samples are from the same source. If “source” means “population”, then probably you shouldn’t use the paired sample t test. But if “source” means the same “subjects” then the paired test is the one you should use. See https://real-statistics.com/students-t-distribution/paired-sample-t-test/ for more details.
2. This is related to the first question. You need to supply more information before I can answer this question.
3. I you are using a right-tailed test then it should never happen that t-calculated is greater than t-critical but p-value is greater than 0.05. If you are using a left-tailed test, then this just means that you can’t reject the null hypothesis.
4. See my answer to your first question.
Charles
Are you beginning with a significance level of 5% or 10% for your 2-tailed test?
What if the value you get is 0.03 for the t-test? For example
TTEST(A4:A13,B4:B13,2,2) =0.03
Do you reject the null hypothesis? What about the 2 tails?
Do large values have to be taken into consideration? What If I get 0.98?
Thank you for your help!
Donna,
The TTEST assumes that alpha = 5%.
If TTEST(A4:A13,B4:B13,2,2) = 0.03 then null hypothesis is rejected since .03 < .05. This is the two-tailed test (since the third argument is 2). If you want the one-tailed test you use the formula TTEST(A4:A13,B4:B13,1,2), which will have a value which is half of the two-tailed test, and so once again you would reject the null hypothesis (since .03/2 = .015 < .05). If you get a p-value = 0.98 you couldn't reject the null hypothesis since .98 > .05.
Charles
Sir,
I have several questions after reading your post.
1. Is there a scientific way (equation or theory) that clearly defines in which case variances of two data sets are equal or unequal?
2. I am not sure if I get your points, if two values obtained respectively from type 2 and type 3 (Excel t test) does not differ greatly, then it suggests equality of variance. If not, the opposite?
3. What does the considerable reduction of df mean in your example? Sorry I am not from background of mathematics. Can you explain to me in details.
4. I have two independent samples, n=6, to compare in excel t test. But I found no evidences to prove their variance equality. Can you suggest some ideas?
Thank you very much for your help. I look forward to your reply.
Have a good day.
Ding
Ding,
1. There are a number of techniques for determining whether variances of two (or more) data sets are approximately equal, including graphical approaches and the commonly used Levene’s test. See the webpage https://real-statistics.com/one-way-analysis-of-variance-anova/homogeneity-variances/ for more information.
2. No, even when the type 2 and type 3 p-values are very similar, the variances may be noticeably different. Generally the variances need to be very different before you will see any real difference between the type 2 and type 3 tests.
3. A smaller value of df changes the p-value. Obviously for the example I have given the smaller value of df doesn’t change the p-value that much.
4. In this case, use the unequal variance test. With such a small sample, there is also risk that the normality assumption may not be satisfied, in which case you may want to use a non-parametric test such Mann-Whitney (see the webpage https://real-statistics.com/non-parametric-tests/mann-whitney-test/)
Charles