Basic Concepts
As shown in Measures of Variability, the coefficient of variation is defined as
where the formula on the left is the sample version and the formula on the right is the population version.
If V is the sample coefficient of variation, then this V is a biased estimate of the population coefficient of variation. In this case, an unbiased estimate of the population coefficient of variation is given by the formula
where n = the sample size. A shorter version is also commonly used, however, namely
Given a sample, we want to estimate a confidence interval for the population coefficient of variation based on the sample correlation of variation and the sample size. It turns out that there are many ways of creating such an estimate. We will consider four such approaches.
Kelley Estimate
This approach uses the non-central t distribution.
First, we define
The Kelley confidence interval is
Naïve Estimate
First, we define
The naïve confidence interval is then
McKay Estimate
The McKay confidence interval is
McKay’s estimate is valid for large values of n (at least n ≥ 10). McKay recommends this estimate only when the coefficient of variation is less than 0.33. Otherwise, McKay’s approximation may not be valid.
Vangel Estimate
Vangel’s modification of McKay’s estimate gives better results for small samples but is still not recommended for V ≥ .33.
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack provides the following worksheet function.
CV_CONF(R1, lab, ctype, short, tails, alpha): returns a 4 × 1 column array with the values: CV of the data in R1, a corrected version of the CV, and the 1-alpha (default for alpha is .05) confidence interval for the CV.
If lab = TRUE (default FALSE) a column of labels is appended to the output. If short = TRUE (default) then the short version of the corrected CV is returned; otherwise, the long version is reported.
Which confidence interval is reported depends on the choice of ctype with values 1 (Kelley, default), 2 (Naïve), 3 (McKay) or 4 (Vangel). These are intervals around the sample V. You can also use the negative of these values, in which case the intervals are around the corrected version of V (short or long, depending on the value of short).
If tails = 2 (default) the two-tailed confidence interval (lower, upper) is returned. If tails = 1, then the two versions of the one-tailed confidence interval are (lower,∞) and (-∞, upper).
Example
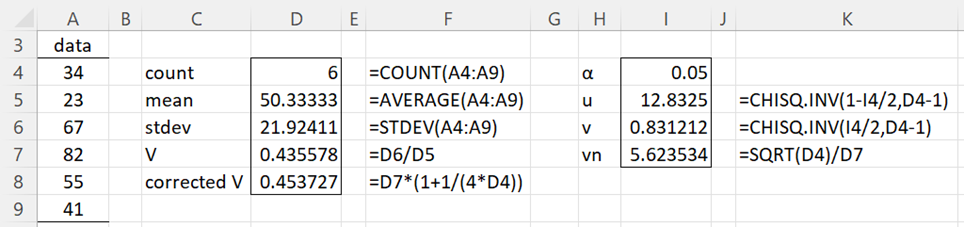
Example 1: Find the 95% confidence interval for the coefficient of variation based on the data in column A of Figure 1. We will consider confidence intervals around the sample V (and not the corrected V).
Figure 1 – CV confidence intervals (part 1)
In Figure 1 we report the shorter version of the corrected V in cell D8. If we had used the long version, then the formula in D8 would be =D7*(1+1/(4*D4)+D7^2/D4+1/(2*(D4-1)^2)).
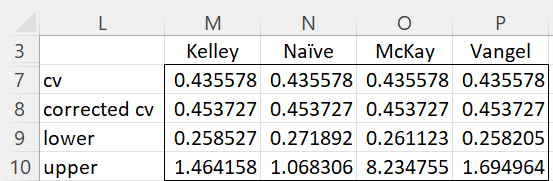
Using the CV_CONF function, we obtain the estimates of the confidence interval shown in Figure 2.
Figure 2 – CV confidence interval (part 2)
E.g. range L7:M10 contains the array formula =CV_CONF(A4:A9,TRUE), which is short for =CV_CONF(A4:A9,TRUE,1,TRUE, 2,.05). If we wanted to use the confidence interval around the long version of the corrected V, we would use the formula =CV_CONF(A4:A9,TRUE,-1,FALSE).
If we calculate the confidence interval manually using the Kelley estimate, we would insert the formula =SQRT(D4)/NT_NCP(I4/2,D4-1,I7) in cell M9 and =SQRT(D4)/NT_NCP(1-I4/2,D4-1,I7) in cell M10.
For the Vangel estimate we would use the formula =D7/SQRT(((I5+2)/D4-1)*D7^2+I5/(D4-1)) in cell P9 and =D7/SQRT(((I6+2)/D4-1)*D7^2+I6/(D4-1)) in cell P10. We could also use the Real Statistics array formula =CV_CONF(A4:A9,,4) in range P7:P10.
References
NIST Dataplot (2017) Coefficient of variation confidence limit
https://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/coefvari.htm
Sokal, R. R. and Braumann, C. A. (1980) Significance Tests for coefficients of variation and variability profiles
https://academic.oup.com/sysbio/article-pdf/29/1/50/4659819/29-1-50.pdf
Beigy, M. (2019) Coefficient of variation
https://github.com/MaaniBeigy/cvcqv
McKay, A. T. (1932) Distributions of the coefficient of variation and the extended ‘t’ distribution. Journal of the Royal Statistical Society, Vol. 95, pp. 695-698.
https://www.jstor.org/stable/2342041
Vangel, M. (1996) Confidence intervals for a normal coefficient of variation. American Statistician, Vol. 15, No. 1, pp. 21-26.
https://www.jstor.org/stable/2685039
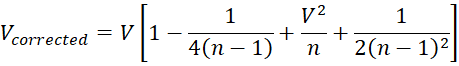
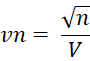
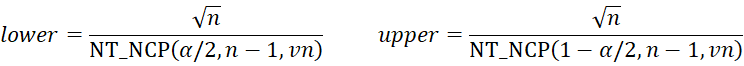
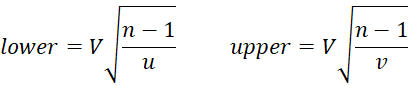
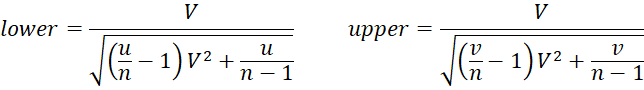
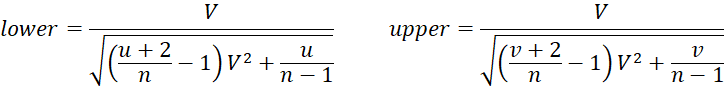
Hi Charles
Thank you for the great help your site is providing.
You have denoted both V (s/av(x)) and Vp (the population CV) by V, which is rather confusing for the equations that follow.
Secondly, what you say is Vcorrected is actually E(V) (expected value of V expressed as a function of sample size and Vp). The truly corrected value of V is the (approximately) unbiased estimate of Vp, i.e. V(1+1/(4n)) (and you describe in “Coefficient of Variation Testing”). In example 1 (Fig. 1) your “corrected V” is actually this unbiased estimate of Vp.
Hi Gudjon,
Thank you for your useful comment. I have made some changes to the webpage to try to clarify things better.
I appreciate your help in improving the clarity and accuracy of the Real Statistics website.
Charles
Doc Thanks a lot