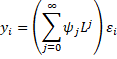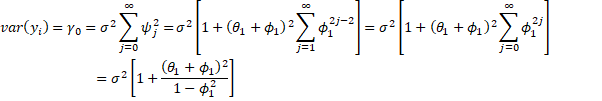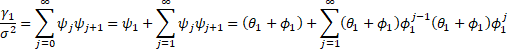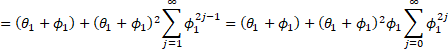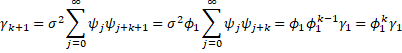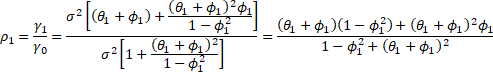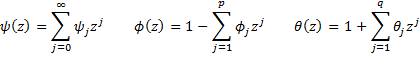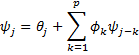ARMA Proofs

Property 1 of ARMA(1,1) Processes: The following is true for an ARMA(1,1) process

Proof: As we saw in Infinitive Moving Average

where ψ₀ = 1 and for j > 0

By Property 4 of Infinitive Moving Average

Property 2 of ARMA(1,1) Processes: The following is true for an ARMA(1,1) process

and for k > 1

Proof: By Property 4 of Infinitive Moving Average

The rest of the proof is by induction on k. First, we note that

By Property 4 of Infinitive Moving Average and the induction hypothesis

Property 3 of ARMA(1,1) Processes: The following is true for an ARMA(1,1) process

and for k > 1
Proof: By Property 1 and 2

Property 2 of ARMA(p,q) Processes: Let

Then

which in turn results in

where θ₀ = 1, θ_j = 0 for j > q and ψ_j = 0 for j < 0.

Proof: Since

If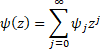converges, then

In this case, we can find the coefficients in ψ(z) by solving φ(L)ψ(z) = θ(L) as follows:

Multiplying out the left side of the equation and equating coefficients of z^j for j = 0, 1, 2, … yields

etc.

which yields the result we are seeking.