Basic Concepts
In paired sample hypothesis testing, a sample from the population is chosen and two measurements for each element in the sample are taken. Each set of measurements is considered a sample. Unlike in two-sample hypothesis testing (see Two-sample t-Test), the two samples are not independent of one another. Paired samples are also called matched samples or repeated measures.
For example, if you want to determine whether drinking a glass of wine or drinking a glass of beer has the same or different impact on memory, one approach is to take a sample of say 40 people, and have half of them drink a glass of wine and the other half drink a glass of beer, and then give each of the 40 people a memory test and compare the results. This is the approach with independent samples.
Another approach is to take a sample of 20 people and have each person drink a glass of wine and take a memory test, and then have the same people drink a glass of beer and again take a memory test, after which we compare the results of the two tests. This is the approach used with paired samples.
Advantages
The advantage of this second approach is the sample can be smaller. Also since the sampled subjects are the same for beer and wine there is less chance that some external factor (confounding variable) will influence the result. The problem with this approach is that it is possible that the results of the second memory test will be lower simply because the person has imbibed more alcohol. This can be corrected by separating the tests in time, e.g. by conducting the test with beer a day after the test with wine.
It is also possible that the order in which people take the tests influences the result (e.g. the subjects learn something on the first test that helps them on the second test, or perhaps taking the test the second time introduces a degree of boredom that lowers the score). One way to address these order effects is to have half the people drink wine on day 1 and beer on day 2, while for the other half the order is reversed (called counterbalancing).
The following table summarizes the advantages of testing with paired samples versus testing with independent samples:
| Paired Samples | Independent Samples |
| Need fewer participants | Fewer problems with fatigue or practice effects |
| Greater control over confounding variables | Participants are less likely to figure out the purpose of the study |
Figure 1 – Comparison of independent and paired samples
Obviously, not all experiments can use the paired sample design. E.g. if you are testing differences between men and women, then independent samples will be necessary.
As you will see from the next example, the analysis of paired samples is done by looking at the difference between the two measurements. As a result, this case uses the same techniques as for the one-sample case, although usually, it is easier to use either the paired t-test data analysis tool or the T.TEST worksheet function with type = 1.
Hypothesis Testing
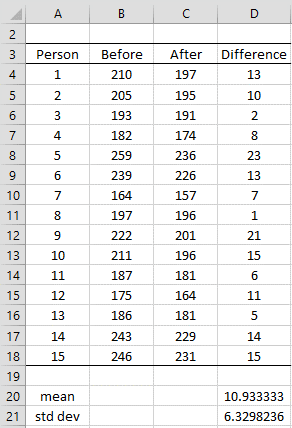
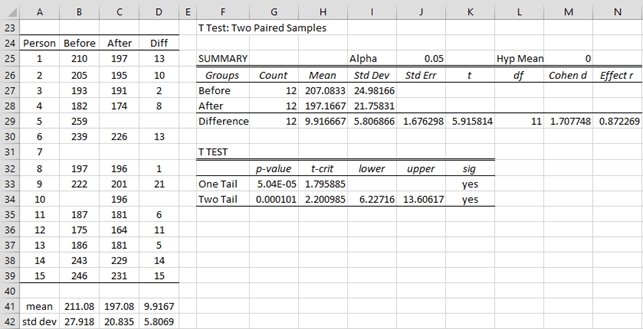
Example 1: A clinic provides a program to help their clients lose weight and asks a consumer agency to investigate the effectiveness of the program. The agency takes a sample of 15 people, weighing each person in the sample before the program begins and 3 months later to produce the table in Figure 2. Determine whether the program is effective.
Figure 2 – Data for paired sample example
Let x = the reduction in weight 3 months after the program starts. The null hypothesis is:
H0: μ = 0; i.e. any differences in weight is due to chance (two-tailed test)
We can make the following calculations using the difference column D:
s.e. = std dev / = 6.33 /
= 1.6343534
tobs = (x̄ – μ) /s.e. = (10.93 – 0) /1.63 = 6.6896995
tcrit = T.INV.2T(α, df) = T.INV.2T(.05, 14) = 2.1447867
Since tobs > tcrit we reject the null hypothesis and conclude with 95% confidence that the difference in weight before and after the program is not due solely to chance.
Alternatively, we can use a type 1 T.TEST to perform the analysis as follows:
p-value = T.TEST(B4:B18, C4:C18, 2, 1) = 1.028E-05 < .05 = α
and so once again we reject the null hypothesis.
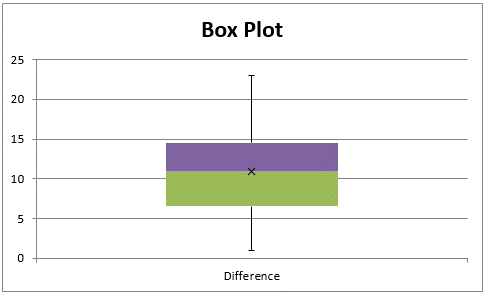
As usual, for the results to be valid, we need to make sure that the assumptions for the t-test hold, namely that the difference measures are normally distributed or at least reasonably symmetric. From Figure 3 we see that this is the case:
Figure 3 – Box Plot for difference measures (column D of Figure 2)
Data Analysis Tools
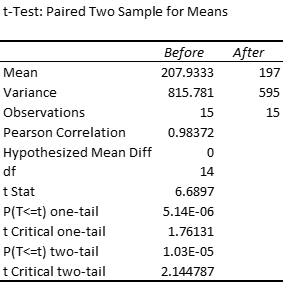
Excel Data Analysis Tool: We can use Excel’s t-Test: Paired Two Sample for Means data analysis tool. The output from this data analysis tool is shown in Figure 4.
Figure 4 – Excel data analysis for paired samples
The Pearson Correlation entry in Figure 4 is explained in Correlation.
Real Statistics Data Analysis Tool: We can also use the T Test and Non-parametric Equivalents data analysis tool in the Real Statistics Resource Pack to get the same result.
To use this tool press Ctrl-m and select T Tests and Non-parametric Equivalents from the menu (or from the Misc tab if using the Multipage interface). A dialog box will appear (as in Figure 1 of t Test Analysis Tool). Enter B3:C18 in the Input Range 1 field (or B3:B18 in Input Range 1 and C3:C18 in Input Range 2) and choose the Column headings included with the data, Paired Samples, and T Test options. When you press the OK button, the output shown in Figure 5 is displayed.
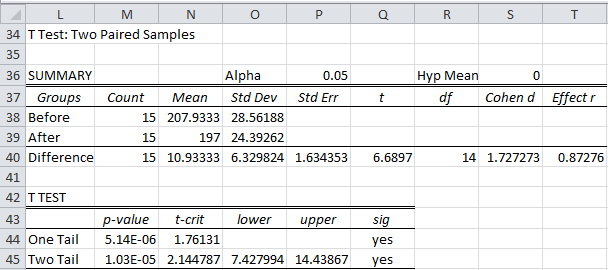
Figure 5 – Real Statistics data analysis for paired samples
Missing Data
The input data for the paired-sample t-test can have missing data, indicated by empty cells or cells with non-numeric data. Such cells will be ignored in the analysis.
Example 2: Repeat Example 1 using the data in range B24:C39 of Figure 6.
In this example, there is missing data for subjects 5, 7, and 10. The analysis is rerun with the data for these people removed. Note that some of the formulas have been changed to account for the missing data. E.g. when there is no missing data, cell H27 can contain the simple formula =AVERAGE(B25:B39), but since there is missing data the following formula is used instead:
=SUMPRODUCT(ISNUMBER(B25:B39)*ISNUMBER(C25:C39),B25:B39)/G27
Figure 6 – Paired t test with missing data
Caution: If you have missing data you can change the data values and even fill in the missing data with numeric values and the resulting analysis will be correct. If, however, the input does not contain any missing data, you can change any of the data values and still get a valid analysis but if you change a numeric value to a non-numeric value then the analysis will not be correct and you will need to rerun the data analysis tool to get the correct results.
Comparing paired samples with independent samples tests
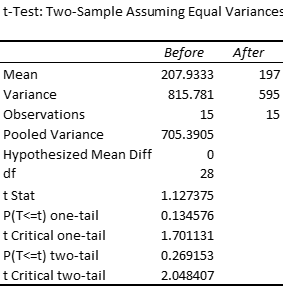
Suppose we run the same analysis for the data in Example 1 from Two Sample t Test with Equal Variances using the t-test with independent samples and compare the results with those we obtained for paired samples:
Figure 6 – Excel data analysis for independent samples
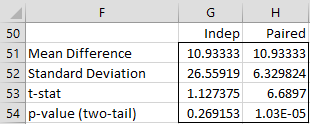
We summarize the results from the two analyses as shown in Figure 7.
Figure 7 – Comparison of paired and independent sample t-tests
Note that the mean differences are the same, but the standard deviation for the paired sample case is lower, which results in a higher t-stat and a lower p-value. This is generally true.
One-sample test
Although Real Statistics provides a data analysis tool for one-sample tests, Excel doesn’t provide a standard data analysis tool for this case. The T.TEST function with type = 1 and the paired samples data analysis tool can, however, be used for the one-sample case by simply creating a null paired sample with all zero data.
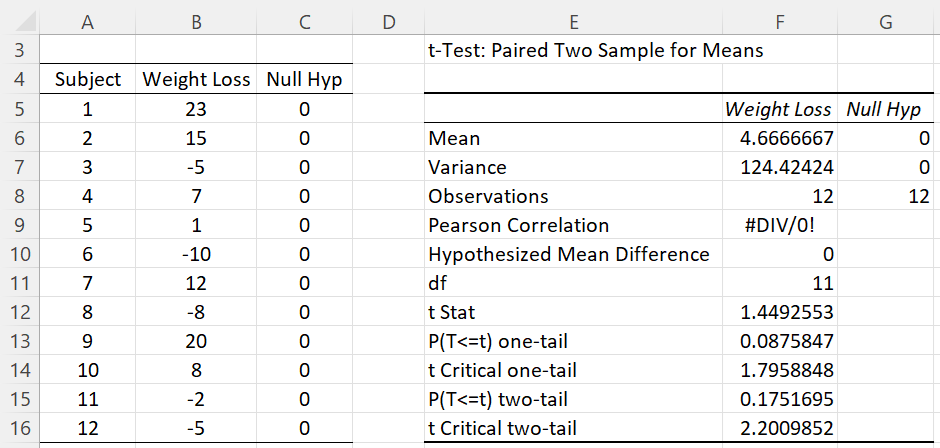
Example 3: Repeat Example 1 of One Sample t-Test using the above observation.
Figure 8 shows how to do this using Excel’s paired t-test data analysis tool.
Figure 8 – Use of paired sample data analysis for one sample test
Effect size
Since the two-sample paired data case is equivalent to the one-sample case, we can use the same approaches for calculating effect size and power as we used in One Sample t Test. In particular, Cohen’s effect size is
where z = x1 – x2. There are other versions of Cohen’s effect size, including drm and dav. These are described at Cohen’s d for Paired Samples.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
Nelson, S. L. and Nelson, E. C. (2016) How to use the t-test data analysis tool in Excel
https://www.dummies.com/article/technology/software/microsoft-products/excel/how-to-use-the-t-test-data-analysis-tool-in-excel-152093/
Zar. J. H. (2010) Biostatistical analysis 5th Ed. Pearson
Greetings, Charles
As always, your website always comes up in various internet searches, and there is always useful infomation that cannot be (easily) found elsewhere.
And of course, your generosity does not end there, given that you always provide help to those who ask.
Here is a question, if I may.
I’d like to run at paired t-test for a set of PRE POST variable , but would like a ONE tailed (positive difference for POST minus PRE) test and CONFIDENCE intervals.
I notice that the output you provide has NO confidence intervals for the one tailed test.
I suppose they should be given as either “lower bound” or”upper bound” only, the latter pertaining to my case.
Here are some questions, if I may, please:
1) Can can one “compare” such outcomes. For a two-tailed test, if both confidence interval boundaries are on either side of ZERO (not crossing it), the diagnosis of “difference” is easy to make… How does it work for ONE-tailed tests?
2) Can one simply change the “alpha” and obtain a two-sided confidence interval,
of which ONE of its boudaries
will have the SAME
as the outer boundery of the one-sided test confidence interval?
Once again, thank you very much for your generous help.
Georgios,
1. If mu represents the population mean, x-bar is the sample mean, se is the sample standard error and crit = T.INV(1-alpha,df), then when H0: mu <= 0 and H1: mu > 0, then the confidence interval is (x-bar – se*crit, +infinity). If H0: mu >= 0 and H1: mu < 0, then the confidence interval is (-infinity, x-bar + se*crit). If 0 is in this interval, then the null hypothesis is accepted. 2. No, because when calculating crit for the two-tailed test, crit = T.INV.2T(alpha, df) = T.INV(1-alpha/2,df) Charles
Many thanks, Charles. You provided 2 key point I could not find in books: ” If 0 is in this interval, then the null hypothesis is accepted”! And that for positive one-tailes, the interval used is that with the lower value to infinity that is used. It now became so clear!
===
I’m working on SPSS, but decided to work with your addins, especially for such issues as one-tailed analyses, etc…
For the paired t-test, you provide effect sizes, Pearson’s “r” and Cohen’s “d”. I’d like to make a diagram such as the following
(http://rpsychologist.com/d3/cohend/)
in my dissertation that will show a score of d = 1.7
I saw such diagrams in another t-test page of yours.
Can a set of two curves be drawn using “real statistics”?
Once again, thanks for everything.
Georgios
Georgios,
You can draw these curves in standard Excel. For curve 1, you create a list of (x,y) coordinates that correspond to a t distribution with the desired degrees of freedom, just as was done for Figure 1 of t Distribution Basic Concept.
For curve 2, you do the exact same thing except that you need to use the same x values but displace the curve (i.e the y values) by the amount that corresponds to d, using the definition of d (essentially you are shifting the mean from zero).
Charles
Charles,
This website is so informative and useful.
I have one participant that I am trying to manipulate behaviour. I have collected 10 sets of data on the same participant (before and after treatment). Basically, I am using a single-case design whereby I measured the participant’s behaviour on 10 different occassions at baseline before treatment. I then measured the participant’s behaviour on 10 different occassions (after treament). Do I use a paired sample t-test for this. Measurements are in time (minute) intervals. Thanks for your help.
Christine,
You can’t use the paired t test because the 10 sets of data are not independent (since they are for the same subject).
Charles
I have just carried out a survey on consumer satisfaction for 7 companies, and I only retain the responses where the respondent has made a purchases from each of the 7 companies. For each case, the respondent is asked to rate (1-10) on 14 items representing consumer satisfaction and 4 items representing consumer convenience. So I will have an individual rating for each item as well as an aggregate score for satisfaction and convenience. Now, if I want to perform a statistical test on whether the individual/aggregate rating for satisfaction and convenience are statistically different from each of the 7 cases, could you advise how I can do so?
If you are using the aggregate score, then you can perform a one-way ANOVA with 7 factors (representing the companies). If there is a significant difference, you can pinpoint where the differences are by using a follow up test (e.g. Tukey’s HSD).
If you have multiple scores per person, then you probably want to consider using MANOVA.
Charles
Hi Charles,
This was a lot of help! Just wondering, if i was analysing three groups- a control, a caffeine group, and an alcohol group, would I still use the paired sample test?
Kindest regards,
Anne
Also, just a little bit more information- I’m testing which group causes more impairment when driving.
Thanks!
Anne,
After performing ANOVA you have two possibilities: (1) there is no significant difference between the three groups, in which the analysis ends and conclude that there is no group that causes significantly more impairment than the others or (2) there is significant different difference between the groups and so you can perform a follow-up test (contrasts, Tukey HSD, etc.) to locate which group causes more impairment.
Charles
Anne,
In general, if you have three different groups, then you would use ANOVA and not a t test.
Charles
I am in a statistics class in college right now. Can someone help me with these problems?
Which problems do you need help with?
Charles
the articles are wow and excellent. I have a question though
If you have 5 groups in your study, why shouldn’t you just compute a t test of each group mean with each other group mean?
I’d be glaf if you answer please.Thanks in advance
Kelvin,
You can, but the experimentwise error will be very high, as explained on the following webpage>
Experimentwise Error
Charles
Hi Charles,
When you compare the 2-Sample test w/ the paired sample test, you state the P-Value for a 2 tailed, 2 sampled test is 0.134576, but I believe that’s the value for a 1 tailed test, and the 2-tailed test is twice that amount.
Jonathan,
Thanks for catching this mistake. The correct values are shown in the Examples Workbook, but not on the webpage. I have now corrected the error. I appreciate your help in improving the website.
Charles
Hi, I’ve conducted a test of 4 different exercises using the same people, and want to calculate the p-vale between exercises to see if the results are significantly different. To put this into context, each exercise measured muscle activation from the gluteus medius and adductor magnus in working and opposite legs. Basically I would like to know what type of t-test to perform to find out if the gluteus medius results from one exercise are significantly different to the gluteus medius results of another exercise, and the same with adductor magnus. All of the data is on Excel.
Your help would be greatly appreciated.
David
Hi David,
If you are using the t test, you should choose the paired sample t test.
You might want to consider using ANOVA, in which case you should look at the repeated measures ANOVA.
Charles
Sir,
I got Mean and standard deviation of a group of subjects before and after treatment respectively, but no individual data, how can I calculate the mean and SD of change?
Thank you
Hello Charles. I’m doing comparing water quality before 2010 and after 2010. I’m using t-test from excel to test it. I also used SPSS to run Mann-whitney U-test on the same data. From SPSS, one of the results showed : “Exact Sig. [2*(1-tailed Sig.)]”. From my understanding, I think SPSS determine it as a one-tailed and thus i need to divide the p-value by 2 in order to get the right sig.value. But how do i know that the results from t-test in excel is in one tailed or two-tailed? If mann-whitney analysis it as one-tailed, should i take the one-tailed p-value for t-test too (say I run on the same set of data).
I’m still abit blur on is it one-tailed or two-tailed. My main purpose is to reject my null hypothesis and say that there IS a difference in the water quality after 2010. this is my scenario.
Jon,
You need to determine in advance of running the test whether you want to use a one-tailed or two-tailed test. This is true for SPSS, Excel or any other test environment. Generally, you should choose the two-tailed test. The one tailed test is chosen if, based on some theoretical reason, only one side of the test is possible — see Null and Alternative Hypothesis for more details.
Charles
1. Thanks for the link. I think I’m doing two-tailed since I’m determining
H0: data set before 2010 = data set after 2010
H1: data set before 2010 ≠ data set after 2010
is my approach correct?
2. For the SPSS results, “Exact Sig. [2*(1-tailed Sig.)]” mean my data can only actually test for one-tailed?
Jon,
1. Looks right
2. Probably correct, but I don’t use SPSS
Charles
Hello,
I am doing a project comparing pre and post test scores of outcome measures for a group therapy. I am limited to the use of Microsoft Excel to undertake statistical analysis. I am sure that I am meant to do a t-test, but I am unsure which one.
My sample is composed of 29 clients who completed the pre and post measures. These were chosen as they completed both measures, as opposed to those that didn’t. So I end up with two columns of 29 scores to compare (29 pairs).
I have run both a ‘t-Test: Two-Sample Assuming Unequal Variances’ and a ‘t-Test: Paired Two Sample for Means’ using the ‘Data Analysis’ function of Excel. The results end up different for both, so I am unsure which one is correct.
After reading this guide, I feel that the ‘t-Test: Paired Two Sample for Means’ is the most appropriate but I don’t trust my understanding enough to decide which is the one to report.
I would be incredibly appreciative if you could clear this up for me, as no one else has yet been able to.
Thank you.
Luke,
Your intuition is correct. The ‘t-Test: Paired Two Sample for Means’ is the one to use.
Charles
Im comparing Qty of Transactions from different age-stage segments (Young, Adults, Mature, etc). Do you think the T-Test Two Paired Sample appropriate?
You can run paired t-tests on pairs of samples (provided you take care of inflated error values), but with more than two samples, you need to use repeated measures ANOVA.
Charles
Dear Charles,
I am analyzing the difference between the financial performance of two kinds of mutual funds over a period of time (vertically for the same kind) pre and post financial crisis and (horizontally for the two kinds). I am analyzing the population of both so, the two types have different number of observations (n). Which basically means that I should use the independent T-test not the matched pair one, based on the fact that the two types have different number of observation along the timeline. Using SPSS and Excel didn’t really help because I have no cut point or grouping variable.
Any help?.
Badr
Badr,
I don-t completely understand your scenario. How many mutual funds do you use in your study? For each what sort of observations are you making (closing price, etc.)? For each mutual fund are you looking at the observations over a multiple time periods. both pre and post financial crisis?
Not sure what sort of cut point or grouping variable you are referring to.
Charles
What an awesome web site! I refer to it often because it has so much valuable information. I am working on a research project and I have two questions Sir. What values go into the TINV function to get the tcrit value? I am testing whether there is a difference between the responses (to the same questions) that business students give versus non-business majors. From your examples, it seems this would be a paired samples test. Does this seem reasonable? Thank you in advance for your time.
Katherine,
I am very pleased that you are getting value from my site. This makes me very happy.
1. The formula =TINV(alpha, df) gives the right critical value for a t distribution with df degrees of freedom at the alpha significance level assuming a two tailed test (critical value at 1-alpha/2). The formula =TINV(1-alpha,df) gives the left critical value (critical value at alpha/2).
2. The paired t test is used when the two groups are related – e.g. (1) data on Monday vs. data for Tuesday for the same subjects or (2) data from two twins or (3) data for the right eye vs data for the left eye for the same people
Here you have business majors vs non-business majors and so you should consider using the two independent sample t test.
Charles
Hi,
I have 2 questions, why would I get a different t value in SPSS and Excel?
2- I have a student who did a pre and post test but messed up the ID numbers so I am assuming we can not do a paired ttest so what type of ttest is the best? Thanks
Hello Charles,
Thanks. This is of great help. I performed a paired t-test for a pre-post analysis. I got a negative -statistic, -3.57 and statistically significant. What does the negative imply? that the post average was lower than pre?
Yasmin,
Yes. If you subtract post from pre you will get 3.57 instead.
Charles
Charles, I am still confused. my post mean is greater than pre mean for all cases but for some the paired samples t-test is negative and others positive. Why? Does the sign matter or do i just check significance level and ignore the sign, and take it to mean post is greater than pre irrespective of the sign?
Thanks a million!
Yasmin,
I’d have to see your data, before I can comment.
Charles
Dear Mr Charles,
I am currently writing a practical write up and I encounter several problems regarding paired t test and outliers. In the experiment, we are comparing two set of data(heart rate, blood pressure etc.) during (1)constant velocity exercise and (2) interval training in the same group of subjects. i.e. each of them did both exercises.
When I was trying to use histograms to test the normality of my data, some of them are only normal when I removed the outliers and transformed. I was trying to use parametric and paired tests to test their significance. Should I include the outlying data during significance calculation? If not, would my data consider as not paired because outliers removed are not in pairs?
Sorry for asking loads of questions but I could not think anymore. Thanks for your time.
Dear Kris,
It really depends on why these outliers exist. If they are true anomalies, then you can remove them and run the test. If instead they are legitimate data elements that are just higher or lower than the others, then it is best not to remove them. If you remove data, you should remove the pair (not just one of the elements in the pair).
The paired t test is pretty robust to violations of normality, and so usually I would just run the t test. If the data is quite different from normal, then I would use a non-parametric test — e.g. Wilcoxon signed-ranks test.
Regarding outliers, when in doubt, run the test both with and without the outliers and report both results.
Charles
Dear Sir, This was very helpful but I’m still confused as to what the best statistic would be for me to use to determine whether a wellness intervention was successful? I have data from 2012 (preintervention) for 60 people followed by annual data in 2013 and 2014 (i.e. blood pressure, weight, total cholesterol, LDL, HDL, smoking status, and activity level –the last two being categorical). I also have data from a number of other people who chose not to participate in the intervention that I would like to use as a control group. At first, I was thinking a matched pairs t-test…then I was pondering a time-series ANOVA. What would you recommend? How can I use all of this data to figure out whether the intervention was successful? Any help would be very much appreciated. Thank you!
Jen,
I would need more complete information about the scenario to give you a definitive answer, but you might find that ANOVA with repeated measures or repeated measures MANOVA to be the appropriate test. These are described on the Real Statistics website.
Charles
Thank you! I reviewed the repeated measures MANOVA and the ANOVA on your site. Your examples are helpful; however, I’m still trying to figure out which statistic(s) I should use. It’s almost as if I have too many factors to compare. For example, on each person I have the following information:
2012 2013 2014
Age 47 48 49
Sex 1 1 1
Highest Grade 6 6 6
Smoking 1 2 3
Exercise 2 2 2
Height 68 68 68
Weight 227 225 227
BP systolic 120 130 120
diastolic 78 82 80
Glucose 307 251 100
Triglycerides 236 219 206
Total Cholesterol 154 158 142
HDL 25 30 33
LDL 82 84 68
Overall Health 3 3 4
Some of the factors I coded such as sex (1=male, 2=female), smoking status, highest grade, exercise habits, and overall health. Would I have to do a repeated measures MANOVA or ANOVA for each factor? I was thinking with the repeated measures ANOVA I could use three factors as you showed. For example, in Excel I tried…
Pre BP Pre Chol Pre Wt/ Post BP Post Chol Post Weight
1
2
3
4
…but then that would only compare two years. So, would I do a 2nd repeated measures ANOVA comparing the next two years…and then pick the next three factors and do the same calculation? If so, how would I make the calculations relate to one another? I truly appreciate your help! Thanks!
Jen
Jen,
I describe single factor MANOVA with repeated measures. It looks like you would need more factors than I currently support.
You should be careful, however, when using such models since they may be quite difficult to interpret.
Before you build such complicated models, you should make sure that you are clear about what hypotheses you are trying to test. Are you really trying to show that there is no difference in all these factors from year to year (in which case a multi-factor MANOVA may be necessary)?
Charles
Hi – great site and information -thank you so much for explaining. However, I have a question concerning my project data: I’ve already taken repeated measures of individuals every 30 second, giving 6 data-points per indivudual (1-150 seconds). Now I want to see if there are significant changes between datapoints for the same individual – i.e. if there is a significant change in values from start to end, or between 30sec and 120 sec.
Do you recomend me to make paired t-tests for samples with unequal (AND equal for checking) variances, or paired t-tests (these are dependent samples- energy penetration is measured over time in human tissue). Should I do this multiple times for each comparison?
In my book (statistics) they write about ANOVA for two or more samples – I did not find any function like this in Excel…??
After all, I want to see if there is any significant change of penetration for each individual. Because individual variations in tissue properties, the SD is big for the group, and the values measured differ very much among individuals – thus not of greatest interest here to compare group means above.
Later, I will compare two different energy sources applied to the same individuals – I then do the same tests as above for each datapoint (i.e. 150 sec)???
Excel does provide various ANOVA data analysis tools, but not a repeated measures ANOVA tool, which is the type that you require. The Real Statistics software does provide this capability along with the follow up tests that you require. See Repeated Measures ANOVA for more information.
Charles
Hi Charles,
I had a question with regard to matched sample data analysis. I have gathered matched data on a popilation. Each set of data is normally distributed. When I perform data analysis on the difference between the matched pair, the date set for this (di) is not normally distributed. A cant perform a T-test if this data is not normally distributed right? If I cant, I went ahead and removed the outliers from the data set and when I run the numbers again, the skewness of (di) is under .05, so the data set is normally distributed. Is that the right way of thinking about this?
If x and y are normally distributed, then x – y is also normally distributed, and so I would have expected the differences to be normally distributed. To use a t test, the data should be normally distributed, but the the test is quite robust to violations of normality provided the data is reasonably symmetric. If the assumptions for the t test are not met you can usually use the Wilcoxon signed ranks nonparametric test. This is described in the website.
You shouldn’t simply remove outliers just to make the assumptions hold. If the outlier is caused by an error or a very exceptional situation, then you might eliminate it. Otherwise you should try to find a suitable replacement test. If this is not possible, then you can eliminate the outlier, but be sure to report that you did this and interpret your results based on the removal of the outlier.
Charles
Hello Charles,
I have a situation that seems to call for a paired t-test, and I was wondering what you’d recommend for a sample size. I want to see if 2 different valuation tools will return a different price for a house. Say I currently use Tool 1, but the assumption is that Tool 2 is more accurate, and thus if Tool 2 returns a significantly different value it would be worth the expense to switch. There are multiple types of houses being evaluated, but the paired t-test would seem to account for that.
Thanks,
Dave
Hello Dave,
The Real Statistics Resource Pack has a data analysis tool which estimates the sample size needed to perform various statistical tests. You need to choose the one-sample/paired t test option. This is further described on the following webpage:
Real Statistics Power data analysis tool
There is additional information on the following webpage:
Sample size requirements for t tests
Charles
Thanks!
Hey Charles!
Great article! I just want to understand if the one-tailed critical value suggests the variable it’s under is significantly greater or lesser?
Yes, depending on whether you are testing against the right (upper) or left (lower) critical value.
Charles
I recently ran choice tests for birds, to see if they preferred either food that they have waited for or food that they have not waited for.
Each of the 8 birds had 15 tests, so I have 120 choices in total. I am logging their latencies to choose either side, and my supervisor said to run a paired t-test.
I have two columns, I am putting the first “wait” latencies in column A of spss and the no-wait in column B of spss. I have 36 values in column A and 84 in column B.
My question is.. Can I analyse two different column sizes? Most birds went for the second choice of not waiting so the not-waiting column consequently has a higher number of values.. n is 36 in the first output so has it only analysed the first column/the first 36 values of both columns?
I am horrible at stats and have tried doing this so many times with the same output.. any (simple) help would be so gratefully received… thank you very much!
Carley,
The columns must have the same size to use the paired t test. I don’t fully understand the situation you are describing, but if say each bird had 15 trials where they waited and 15 trials where they didn’t wait, you could create a score for the wait case and a score for the non-wait case and use these in the paired t test (in this case you would have 8 pairs of scores). Caution: this may not be your situation.
Charles
Hello, I am doing a comparison of two portfolios by comparing the series of sharp-ratios, will this be a independent or dependent t-test?
I am not that familiar with the Sharpe ratio, but a quick look on the Internet indicated that there are a lot of papers about how to compare sharpe ratios using a t test. From what I can tell, the test is neither the classical independent nor dependent t test. In any case, there are many references to how to conduct various tests based on the t distribution.
Charles
sir, i am working in the privatization and want to find out the mean diffrence between public and private sector banks, should i use paired sample test or two smple test … plz help me
It sounds like an independent samples test. Depending on the details, it could be a t test, ANOVA, MANOVA or some other test.
Charles
Thanks for this helpful article.
In my experiments i have 3 measurements before treatment and 3 after treatment. However these are the same sample measured three times (triplicates).
Would this paired t-test still work?
And is the size (3) too small?
Thank you!
Sam
Sam,
A sample of size 3 is quite small and so the power of such a test would be very low. Also size all the measurements are on the same subject, you don’t have the required independence to even use the paired t test.
Charles
I am trying to understand how to interpret the critical values of t-distribution. When I read about the t-test it says if the value is higher than the critical value then you reject the null, but I have written in notes from a course (and see it written here) if it is lower you reject the null. With practice data I entered into excel, the value is coming out to .09e-6 which I understand the e means it is 10^-6. (with 10 samples). I am either misreading or misunderstanding the interpretation of that value or both?! Any suggestions?
In a two tailed test, there are two critical values, one on the right side of the distribution and another on the left side of the distribution. You reject the null hypothesis if the statistic is less than the left critical value or greater than the right critical value.
There are two versions of a one tailed test. In one you reject the null hypothesis if the statistic is less than the left critical value. In the other you reject the null hypothesis if the statistic is greater than the right critical value.
See Hypothesis Testing for more details.
Charles
Dear Sir,
I have a question. If the Box-Plot is not normally distributed (severely one-sided based on BoxPlot), does it mean that paired t-test cannot be used / invalid (assumption for paired t-test: normal distribution)? What about Wilcoxon signed rank test? I tried Wilcoxon signed rank test and found that p > 0.2. This is very similar to paired t-test where p > 0.19.
Thank you.
Sincerely,
Yoga
Yoga,
These tests are fairly robust to violations of the assumptions, but if the data is severely skewed, then you should consider using the sign test.
Charles
Yoga,
The paired t test requires that the paired differences be normally distributed. Two things to note: (1) the two samples don’t need to be normally distributed, just the difference values and (2) the test is fairly robust to violations of this assumption, especially for relatively symmetric data, but if the data is severely skewed then the test is not so robust.
Wilcoxon signed ranks test also depends on the data being relatively symmetric.
The sign test does not assume symmetry and so you this might be your best choice, even though its power is not so high (and so you might need a large sample to avoid high type II error).
You can also investigate using a transformation which will make the data more normal (t test) or at least symmetric (sign-rank test).
Finally, you should make sure that the data is not severely skewed due to outliers. In this case, you still be able to use Wilcoxon signed ranks test.
Charles
Dear Charles,
I have a question. What should I do for a case when there are pre- and post test scores measured, but there are missing values for some of the pre- scores and some of the post- scores.
First I wanted to remove the paires with missing values, but in this case it is difficult to remove them, because there are too little measurements. Is it possible to use a two-sample t-test in this case, whithout removing any data. Or is there another test which I can use?
Thanks,
Henriette
Henriette,
The only approach I am familiar with is to delete any pairs with a missing value. I came across the following approach, however, which may be helpful to you.
https://sph.uth.edu/courses/biometry/Lmoye/PH1820-21/PH1821/misttest.htm
Charles
Thanks for your reply!
Unfortunately, it is very complicated the way they solve it in the link you sent me.
Dear Charles,
I have a question.
What should I do for a case where two different numbers of participants (i.e. two subgroups with different Ns) from the same group took two tests. So, let’s say I have Group T (N=30), but 23 and 20 out of Group T took two different tests (Test A and Test B), and I want to test the difference between the scores from Test A (N=23) and Test B (N=20). I think I should do a (independent) two-sample t-test for this case. But I also want to make sure whether there is any way to use paired-t test for it (because Test A and Test B were actually from the same Group T). Thanks for your comments in advance,
Thanks for your
As long as the A and B groups were selected randomly from group T you can use the two independent samples t test. But no one in group A can also be in group B. If you have overlap between the two groups then neither t test is appropriate. In fact, I know of no test that would be appropriate.
Charles
Thank you very much for your prompt reply!!
Very helpful and clear explanation. Thank you.
I’m trying to interpret a data set with 187 pre and post test scores – the hypothesis being that scores will increase from beginning to the end of the year. The means are 42 and 66 for pre and post, but the paired sample t-test returns a negative value for the t-stat (-23.3591). What does this mean?
I think I can see what that negative value means – it’s the difference between pre and post means. So instead of the difference being zero which is the null hypothesis, and the negative number indicates that the post test score incraesed.
So I guess I answered my question.
Yes, that is correct.
Charles
this was really nice
Thank you for this webpage– very helpful!!
Is there a way to do a repeated measures with 3 time points? I’m comparing means at pretreatment, posttreatment, and 3 months posttreatment.
Grace,
Yes, it is called ANOVA with Repeated Measures.
Charles
Hi I was wondering what test I should use if I am trying to compare the ages of people and their life expectancy.
Thanks
Brandon,
It depends on what you mean by compare. Generally this is like comparing “apples” with “oranges”. Perhaps you mean that you want to correlate ages and life expectancy, in which case you probably want to use one of the correlation tests. Or you might want to predict life expectancy based on a person’s age, in which case you would use regression.
Charles
I want to do pre and post test of anxiety and the effect of exercise on anxiety. Is this a good use of Paired Sample t-test? Or should I be using TWO SAMPLE T –TEST WITH PAIRED SAMPLES?
thanks,
S. Self
One of these is the standard Excel data analysis tool and the other is the Real Statistics data analysis tool. They should yield the same results, although the Real Statistics tool provides some additional information.
Charles
Hello,
I would please have a simple question. I need to run a paired t-test between groups of different sample size. Do I need to extend my smaller array to the same size of the largest one? Or do I need to reduce the largest one, excluding some data?
Thank you in advance,
Stefano
please help me…
can we use paired t-test for 450 samples also…
If by 450 samples you mean two samples with 450 elements, then the answer is yes. If you mean 450 samples, then the answer is no. Instead you should use ANOVA with repeated measuress.
Charles
Just out of curiosity. I have many different blood values to analyze. I have set up all the worksheets in a workbook exactly the same way. Is it possible to have a t test run on an entire workbook or do I have to do an individual t test for each worksheet?
Thanks
Charles
I love your website and it has been very useful for me. I have recently downloaded the real statistics download that you provide and have a question. I am comparing the blood values of test subjects in a clinical trial such as WBC before and after a drug. The tests subjects are the same. Under the t test and nonparametric equivalents which option would be best: one sample; two paired samples; or the two independent samples? I am looking to see if the difference is significant.
Sorry if this is a novice question.
Many Thanks
Charles
Charles,
If you are testing the same subjects before and after then you should use a paired samples test.
Charles
Thanks for the quick reply. That is the one that I have been using. Awesome website. Once again Thank you
BTW – Pretty cool first name.
Charles
Hi, I’m doing a lab in order to see the effect of hand dominance on reaction time. I tested 15 people, each of them doing 5 trials. If I average out the reaction time trials for the dominant hand and non-dominant for each person, would I use a paired sample t-test to compare the means(for example, my average reaction time for my right hand is 0.553 s and 0.883 s for left hand, to compare these two values)? Or would a independent t-test be more suitable?
Lana,
If you are testing the right and left hands of the same people, then you should use the paired sample t-test.
Charles
I’m looking at pretty much the same situation.
Looking at the data of dominant versus non dominant hand from the same people.
Seeing as it isn’t a before and after test and just a which hand is faster test wouldn’t it be independent?
Also if the data is incredibly skewed will that change which test I would use?
Just one other thing I know I need a one tail test but I’m still trying to figure out if it is upper or lower.
Matt,
If the mean of the differences between sample pairs is negative then you are typically dealing with a lower tail. If it is positive then you are dealing with an upper tail. The test is whether the population mean is zero.
Charles
Matt,
Since the right hand and left hand are owned by the same person, the pairs of values are not independent, but dependent, and so for this reason a paired test is used. The before and after types of situations are probably the most common paired tests, but others also occur (e.g. husbands vs. their wives).
If the assumptions for the test are not met you might use the paired Wilcoxon Signed-Ranks test instead of the t test.
Charles
Thanks so much for the reply.
It has been incredibly useful.
My sample size is 125 and the data is incredibly skewed to the right however the differences of the two samples is approximately normal. Will chance my choice of test?
Matt,
Since the test is on the differences between the two samples, you should be able to use a paired t test. If you use the Wilcoxon Signed Ranks non-parametric test the results should be similar.
Charles
Great website!!
I have a similar situation, seeing if a metric like reaction speed changes with a device ON vs. OFF. We have 37 subjects test ON five times and OFF five times. How would we use the repetitions of the test to increase our statistical power? One ON vs. OFF test one 37 different people would be a paired t-test, but if each person had multiple repeats can we use that somehow, like get a better feel for the st dev of the population? Thanks!
Glad you like the website.
You could perform a two factor repeated measures ANOVA where both factors are repeated measures (factor A = ON vs. OFF and factor B is trial 1, 2, 3, 4, 5). I don’t know whether this will improve power, but you can try some experiments yourself.
Charles
Hi Charles, great tutorial!
I am used to using SPSS so Excel is a bit of a change. I just ran a paired samples t-test with a large-ish sample size (1403) following your directions and it’s saying the p one-tail is P(T<=t) one-tail 1.77E-07 I'm not sure how the p value can be greater than 1 or how to interpret this. Any suggestions would be helpful and I apologize if this is a silly question.
Thanks!
Mandy,
1.77E-07 = 0.000000177, which is a very small positive number less than 1.
Charles
Hi Charles,
Thanks! But how did you calculate that? Does the E-07 mean to move the decimal over by 7? Sorry for all of the questions 🙂
Mandy,
Yes. 1.4E-07 is the same as 1.4 times 10 raised to the -7 power (which means move the decimal over 7 places). E stands for exponent.
Charles
Thank you Charles. Great site!
Is this technique suitable for determining whether a simulation of a ball trajectory is ‘close enough’ to a measured trajectory?
Rather than columns A, B and C being “Person”, “Before” and “After” could they be replaced with “Time”, “Height (test)” and “Height (simulation)”? In your example the weight of each person is independent of the person before, but in my example the time is dependent upon the one before. I would really apprecaiate any advice!
Toby,
You can use Chi-square Goodness of Fit. See Goodness of Fit.
Charles
sir
i need your help for my research data analysis. i applied paired sample t-test for pre-test post test comparison. mean differences r very high i.e n=8 pre-test mean =41.25 post test mean= 71.25
mean=-30 , t -value is= -13.09, df =7 sig (2 tailed )=0.000 at .05
for another test
mean =-17.750, t= -20.139, df=7, sig =0.00 at .05 level
plz guide me what to do and how to defend my work
When you say that for another test you get a different result. Is this for the same data using a different test? If so which test did you use for this other test? If it is for different data, then I don’t understand your question; please provide more information.
Charles
nice data very professional in your presentation
comment not capturing second part of question- if p lt 0.05 two tailed and p gt 0.05 one tailed, what is conclusion?
Jeff,
You are supposed to decide on the type of test (one-tail or two-tail) before you collect the data or run the test. If you believe very strongly that the lower or upper tail of the distribution is highly unlikely then you would use a one-tail test. Generally the default (at least for most tests) is a two-tailed test.
For a symmetric distribution if you get say p-value = .04 for a one-tailed test, then the p-value of the two-tailed test will be .08. It is certainly possible to have a significant result for a one-tailed test (i.e. you reject the null hypothesis), while a non-significant result for a two-tailed test (i.e. you cannot reject the null hypothesis). The reverse is not true (since the p-value for a two-tailed test greater than or equal to the p-value of the one-tailed test).
I would say that if you haven’t decided prior to running the test whether you are using a one-tailed or a two-tailed test, then you should use the result of the two-tailed test (unless it is clear that you should have seen that one tail of the distribution was highly unlikely or impossible).
Charles
Sorry,. Question should have been-
Regarding t-test mean comparisions in general; at 95% confidence, if the two-tailed value had come out 0.05, what would be the conclusion. Could this happen?
Hello Charles,
Regarding t-test mean comparisions in general; at 95% confidence, if the two-tailed value had come out 0.05, what would be the conclusion?
Thank you.
-Jeff
Sir,
I could not understand – p-value 1.028E-05 < .05 = α
What is the meaning of E in it and how it is less than .05?
thanks
E-05 just means ten raised to the minus 5th power. This is the notation that Excel uses.
Charles
great really!!!
Sir, please if you could be so kind as to help with one question that troubles me. You said that paired samples can be protected easier from cofouding variables. What if (in my case), I cant get reed of a cofouder, but I would like to perform some kind of correction to the paired samples t-test. To be more specific: in dialysis patients as days from dialysis session pass, their blood pressure rises and their arterial stifness seems to rise also. How could I correct my findings regarding arterial stifness, taking into account that blood pressure might be a cofunder and correct for that? Is it posible to perform that with SPSS? or Excel? is it possible anyway?
Thank you for your kindness
With Respect
Pavlos Malindretos
Pavlos,
I don’t have a precise answer for you, but I will provide some reflections:
(1) If blood pressure is highly correlated with arterial stiffness, then maybe there is no need to adjust for blood pressure since they are essentially measuring the same thing.
(2) Assuming that blood pressure is a confounding factor that needs to be corrected for, how you do the correction depends on what you are trying to test (e.g. there is a significant degradation in arterial stiffness as a patient undergoes more days of dialysis).
(3) There is a technique called Repeated Measures ANCOVA which may be appropriate for your needs. It is supported in SPSS.
Charles