Fitting a Weibull Distribution via Regression

Basic Concepts

Another approach to finding the parameters for a Weibull distribution is based on linear regression. First, note that the cumulative distribution function of a Weibull distribution can be expressed as

Weibull cdf

and so

Taking the natural log of both sides of the equation yields the equation

Multiplying both sides of the equation by -1 and then taking the log again yields the equation

This can be expressed as the linear equation

where y = ln(–ln(1–F(x))), x′ = ln x and a = –β ln α. Thus if the sample has a Weibull distribution, then we should be able to find the coefficients via linear regression. We now show how to do this in Excel using the SLOPE and INTERCEPT functions.

Examples

Example 1: Repeat Example 1 of Method of Moments: Weibull Distribution using the regression approach described above. The data is repeated in range B4:B15 of Figure 1.

Fitting Weibull via regression

Figure 1 – Fitting a Weibull distribution via regression

First, we sort the data (e.g. by using the Real Statistics array formula =QSORT(B4:B15)) in column C. Now the x values in the regression are the values of LN(x), i.e. the values in column D. To get the y values, first, we calculate the estimated values of F(x) by placing the formula =(A4-0.5)/A$15 in cell E4, highlighting the range E4:E15 and pressing Ctrl-D. This is similar to the approach used to create a QQ Plot as described in Graphical Tests for Normality. Alternatively, we could use Benard’s approximation by inserting the formula =(A4-0.3)/(A$15+.4) in cell E4.

Next, we enter the formula =LN(-LN(1-E4)) in cell F5, highlight range F5:F15 and press Crtl-D. The y values for our regression are those found in column F.

We now estimate β parameter to be 3.746 using the slope of the regression line (cell I3 of Figure 2) and α to be 692.088 using the intercept of the regression line (cells I4 and I5 of Figure 2).

From the scatter chart shown on the right side of Figure 2, we see that the Weibull distribution is a good fit for the data (i.e. the linear trendline aligns pretty well with the data elements).

We also see that the R-square value is quite high (cell I13) and the sample mean and variance are quite close to the theoretical values determined by alpha and beta (range I7:I8 and I10:I11).

Estimating Weibull parameters regression

Figure 2 – Using regression to calculate the Weibull parameters

Worksheet Functions

Real Statistics Function: The Real Statistics Resource Pack contains the following array functions that estimate the Weibull distribution parameter values which fit the data in range R1 based on regression. R1 is a column array with no missing data values.

WEIBULL_FITR(R1, lab, benard) = returns an array with the Weibull distribution parameter values and the R-square value. If lab = TRUE, then an extra column of labels is appended to the output (default FALSE). If benard = TRUE (default) then Benard’s approximation is used; otherwise, the version described above is used. MLE is the LL value corresponding to the alpha and beta parameters.

For Example 1, Figure 3 shows the output from the array worksheet formula =WEIBULL_FITR(B4:B15,TRUE,FALSE), while Figure 4 shows the output from the array formula =WEIBULL_FITR(B4:B15,TRUE) (the version with Benard’s approximation).

Weibull regression fit function

Figure 3 – Output from WEIBULL_FITR without Benard approximation

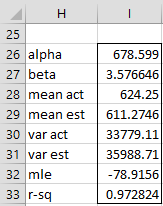
Weibull fit regression Benard

Figure 4 – Output from WEIBULL_FITR with Benard approximation

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Evans, J, W., Kretschmann, D. E., Green, D. W. (2019) Procedures for estimation of Weibull parameters
https://www.fpl.fs.usda.gov/documnts/fplgtr/fpl_gtr264.pdf

Dorner, W. W. (1999) Using Microsoft Excel for Weibull analysis
https://www.qualitydigest.com/jan99/html/body_body_excel.html

ReliaWiki (2019) The Weibull distribution
https://www.reliawiki.com/index.php/The_Weibull_Distribution

NCSS (2017) Distribution (Weibull) fitting
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/NCSS/Distribution-Weibull-Fitting.pdf

62 thoughts on “Fitting a Weibull Distribution via Regression”

  2. Charles,

    Thank you very much for your informative article.

    Previously, I have used Excel to produce a histogram, then used a least squares method with solver to fit a Weibull distribution, using an additional column.

    What I don’t understand from your method, is why F(x) is the rank of the data point divided by n, i.e. the canonical position in the list (from 0 to 1). F(x) from the original formulae is the Weibull distribution itself. I’m missing something fundamental here…

    Paul

    Reply

    • Hi Paul,
      This is a commonly used approach for estimating the cumulative distribution function F(x). This is also used by the Kolmogorov-Smirnov test and the Anderson-Darling test.
      Charles

      Reply

  3. Charles,

    Please could you include examples with multiple examples of censored data. I don’t think the method of moments works with censored data but ranked regression and MLE do, If we are trying to calculate reliability with components that have scheduled replacements (that have variance in the ages they are changed) and taking into account the age of the components currently fitted, (all censored data) as well as the ages when the components fail, we should get better results

    Reply

  4. Hi Charles,

    I had a bit of a question about fitting probability density functions (specifically the Weibull Distribution) to a set of data, although it is in a different case to the one you discussed, I was still hoping you could help me. I have seen a number of examples where the distribution is directly overlaid on the histogram and they both share the same axis titles and I don’t fully understand why this is, specifically with the y-axis.

    From my understanding, the y-value for the distribution is the probability density, which can be described as the rate that the probability is changing over the unit that x is (or the probability per x). The y-axis for the histogram is simply the number of times that a specific outcome has occurred, so I am not entirely sure how these two can be equated. Should the axis titles be different? I’m not entirely sure why the standard layout seems to be sharing the same axis title?

    Reply

    • Elisabeth,
      If you had a very large sample and your histogram had lots of bars then the histogram would match the distribution graph quite well. Of course, the units on the y axis would be different. For the histogram, the units are frequency numbers. You can think of the perfect histogram as slicing the area under the distribution curve and the x-axis into lots of rectangular bars. In fact, as the width of these bars approaches zero the histogram would fill up this area perfectly.
      For the normal distribution (instead of the Weibull distribution), this process is illustrated at
      https://www.real-statistics.com/distribution-fitting/kernel-density-estimation/
      Charles

      Reply

  6. Hi
    Is it possible to use this method for other distributions? I currently use for the exponential, Weibull and log-logistic but would also like to use it for lognormal, generalised gamma and gompertz if possible.

    Reply

    • Hello Keith,
      Yes, it is possible to use a similar approach for some other distributions, but I have not yet implemented these as yet. The Maximum Likelihood approach has been implemented for a great many distributions, but not yet for generalized gamma and Gompertz.
      Charles

      Reply

  7. Dear Charles,

    Thanks for the great explanations

    What about fitting nonlinear regressions by minimizing the least squares with Solver? Isn’t that an option for any regression, expanding from Weibull to Gompertz, Lognormal, Logistic etc?

    Regards,

    Ivan

    Reply

  8. Dear Charles,

    thank you so much for your helpful example. I would like to extend it with a weigth ‘w’
    where w := [(1-F(x))log(1/1-F(x)))]². I calculated the weigth factors but, since I am not an expert in statistics, I don’t really know at which point I would have to apply the multiplication with w.

    Can you aid me on this one ?

    Thanks and kind regards
    Lucas

    Reply

  9. Dear Charles, I really appreciate your explanation.

    I’m trying to fit data to a distribution with the expression: a*(1-exp-(x/b)^c), and I found difficult to take care of the a parameter in the linealization of the expression. Do you have any ideas?

    Thank you very much

    Reply

    • Are you trying to create a linear regression model for y = a*(1-exp(-(x/b)^c)) ? If so, are a, b and c fixed constants or coefficients to be estimated?
      Charles

      Reply

      • Yes, a, b and c are coefficients to be estimated. I was trying to estimate them as you calculated alpha and beta in this post, but not sure about a.

        Thank you very much

        Reply

        • Andres,
          I don’t know how to take care of the a coefficient using linear regression. You might need to use non-linear regression (e.g. using Solver or Newton’s method).
          Charles

          Reply

          • Dear Charles, thank you very much for your kind reply. I’m trying to fit my values using Newton’s method. Thanks

  10. Dear Charles. Thanks a lot for the exercise. I have done it in stata as well and it is perfect for teaching Weibull’s distribution.
    Just an additional question. Could you help me to get the fitted values but in it’s original “x” values? I had no problem in doing that with the exponential distribution, but I’ have been hours trying it for Weibull distributions but unfortunately can’t achieve them.

    Regards

    Reply

  13. Charles,
    Will you please check the logic included in the Real Stat Analysis Tool for the Weibull distribution with censored data? The alpha and beta rendered using the system produce the same alpha and beta values without censoring data.

    Thanks,
    -Sun

    Reply

    • Sun,
      Can you give me an example where the data analysis tool produces the same alpha and beta values with censored data and without censored data?
      Charles

      Reply

      • I used the same data provided in the example on the web with n=12, ncensor=2, and censor=900.

        without censored data using the method of MLE:
        alpha= 689.8070722
        beta= 4.141937628
        mean act = 624.25
        mean est= 626.4900006
        var act= 33779.11364
        var est= 29001.55648
        mle= -78.83963515

        with censored data using the MLE and Sover:
        alpha 755.03769
        beta 3.55435801
        n 12
        m 2
        T 900
        MLE -83.50895892

        with censored data using the Real Stat Analysis Tool with the censor options:
        iterations 20
        censor 900
        count 2

        alpha 689.8070752
        beta 4.141937786
        mean act 626.4605309
        mean est 626.4900046
        var act 29028.04921
        var est 29001.55485
        mle -78.83963518

        Thanks,
        -Sun

        Reply

        • Hello Sun,

          Sorry that it has taken me so long to respond. I started to look into this a few weeks ago, but then got distracted with other things. Using the latest version of the Real Statistics software, I get the following results when using =WEIBULL_FIT(A4:A15,TRUE,20,4,D4,D3) with censored data. These results are the same as the results from Solver but different from the non-censored case.

          alpha 755.0382616
          beta 3.554355741
          mean act 678.6938455
          mean est 679.9019237
          var act 48784.89265
          var est 45027.33003
          mle -83.50895892

          I can’t recall whether I made any changes to the software a few weeks ago based on your comments.

          Charles

          Reply

  15. Hi Charles,
    I installed the Real Statistics Resource Package
    latest version: 6.1 Excel 2010/2013/2016/2019/365 Windows
    I use Excel 2013.
    When I tried your example, x column in figure 1, using WEIBULL_FITR(B4:B15,TRUE,FALSE)
    I get “alpha” in the cell but not additional number or text in other cells.
    Thanks
    Mario
    Mario

    Reply

  16. It appears that everything in Figure 2 is right, but there is a formula you give that doesn’t match the equation you used in Figure 2, cell H4.

    Given:
    ln(–ln(1–F(x))) = β ln x-β ln α
    and
    y=βx′+a

    I understand that:
    y = ln(–ln(1–F(x))) and
    x′ = ln x

    But should α = β ln x
    actually be a = -β ln α,
    which would yield and estimate for α as
    α=exp[-a/β],
    where a is the intercept of the regression line as you correctly display in Figure 2.

    Reply

    • Dear Kevin,
      Thank you for finding this error. I completely misstated the expression for the intercept a. I have now corrected this on the webpage. Please let me know if I have missed something else.
      I really appreciate your help in improving the Real Statistics website and making it easier for people to understand the underlying concepts.
      Charles

      Reply

  17. Thank you for this wonderful work on the Weibull distributions, as a reliability engineer this is really useful. The Abernethy book ‘The Weibull handbook’ provides a lot of insight into how engineers use Weibull. I would like to request that you produce some goodness of fit methods for the Weibull, but also show how this regression method may also be used with right censored data. I would like to see your work here reproduced in Python, especially using the Jupyter notebook formats so all of the explanations and formulas can be seen juxtaposed with the code. Would you give permission for this?

    Reply

    • Charles,

      Thank you for your kind words.

      The website already includes goodness of fit methods. See
      Anderson-Darling Test
      Chi-square Goodness of Fit Test

      I investigated using the regression approach for Weibull distributed data, including right censored data. I wasn’t entirely happy with the approach, and so I decided to perform this using the maximum likelihood approach. See
      Weibull with Censored Data
      Fitting Weibull Parameters via MLE
      If you have a good reference for doing this via regression, I would be happy to look at it.

      What sort of permission do you need to reproduce the Real Statistic work in Python?

      Charles

      Reply

      • Your permission to make any python code using the methods you describe in your site (not Python calling excel) freely available on Github. Obviously, if I do anything I would acknowledge you and this website.

        Reply

        • Dear Charles,
          I am quite pleased that the code that you created was based on things that you learned from the Real Statistics website and would be honoured to get your acknowledgement.
          Charles

          Reply

          • x ln(x) F(x) ln(F(x)) ln(-ln(1-F(X)))
            1 315 5.752572639 0.041667 -3.178046 -3.156841
            2 386 5.955837369 0.125 -2.079442 -2.013419
            3 487 6.188264123 0.208333 -1.568618 -1.454083
            4 509 6.232448017 0.291667 -1.232143 -1.064672
            5 512 6.238324625 0.375 -0.980829 -0.755015
            6 613 6.418364936 0.458333 -0.780159 -0.489221
            7 680 6.522092798 0.541667 -0.613104 -0.248257
            8 725 6.586171655 0.635 -0.454130 0.007827
            9 753 6.624065228 0.708333 -0.344841 0.208755
            10 811 6.698268054 0.791667 -0.233614 0.450195
            11 848 6.742880636 0.875 -0.133531 0.732099
            12 872 6.770789424 0.958333 -0.042560 1.156266
            Hi Charles,
            Sorry I could not paste the chart .
            Just thought that would power law ln- ln chart be an alternative for regressing failure -time? Much appreciate your comments.

      • This looks very interesting and rather an advance on my more primtive OLS fitting in Excel.
        One problem I’ve been struggling with is to estimate precision around Weibull (and other distribution) parameters for right censored and full data sets.
        Does/ Could your package permit estimation of SEs for alpha beta (or lambda(slope) gamma(shape) as I would call from (from Collett 2004)? I read somewhere that MLE can be used to this purpose…

        Thanks

        Reply

        • Hello Jack,
          This is an excellent question. I know of three methods for estimating the standard error and confidence intervals for distribution parameters: (a) exact method (can only be used for a few distributions), (b) an approach based on some large sample properties and (c) simulation.
          Real Statistics currently only provides support for (a), but this is not applicable for most distributions.
          I plan to add support for (c) shortly (probably in the next release) and maybe even (b).
          Charles

          Reply

  18. This was quite helpful, in getting started on developing a solution in Excel for creating Weibull plots. I wanted to understand the underlying estimator and regression. It is helpful to note that the formula used to estimate the values of F(x) in column E belongs to the method of symmetric cumulative distribution function. There are other possible estimators, such as the mean rank and median rank (used by Dorner, 1999). To get a look into the math of the estimator and regression methods, see the 2014 paper “A Comparison of Methods for the Estimation of Weibull Distribution Parameters” by Nwobi and Ugomma. It is freely available online. They conclude that the mean rank (MR) gives the best estimates for a two-parameter Weibull distribution, and that the maximum likelihood estimation (MLE) is preferable over the method of moments and least-squares methods. Good stuff!

    The Excel implementation I come up with should be freely available, so I will post a link here to my solution once it is finalized.

    Reply

  19. I m quite confused about the terminology. Are the least square, the graphical and the regression method all the same as stated above ?
    Thanks

    Reply

  21. Hello i am following your website and found it very useful but at some place got some confusion. for the X values 308,362,364,376,470,470. Now if we go by the suggestion given in figure 2, it has different results while from WEIBULL_FITR it is giving different results… am i missing something ?

    Weibull_FLTR Excel native formula
    alpha 419.0054967 510.1082484
    beta 6.764077297 5.401703329
    mean act 391.6666667 391.6666667
    mean est 391.2498584 470.4495904
    var act 4232.666667 4232.666667
    var est 4605.423387 10080.40283
    mle -33.48598565
    r-sq 0.875813349 0.835018325

    Reply

Leave a Comment