ARMA Tool Options

We now describe the following options that are displayed in Figure 1 of Real Statistics ARMA Tool.

• Make AR(p) agree with OLS
• Include sigma-sq in AIC/BIC
• Reformat for Linear Regression
• Use Solver

Also, note that the Differences field is described in ARIMA Differencing and ARIMA Model Coefficients.

Use Solver: If this option is selected then the ARIMA_Coeff function is not used to estimate the ARIMA coefficients, but instead Solver is used as described in Calculating ARMA Coefficients using Solver.

Make AR(p) agree with OLS: The usual calculation for the statistic (e.g. cell J15 of Figure 2) is to take the square root of SSE/n. If we are modelling an AR(p) process, then it is common to use an ordinary least squares (OLS) regression, in which case, s.e. = =  if there is a constant term and s.e. = =  if there is no constant term.

If you check this option then the OLS regression approach is used for an AR(p) model; otherwise the  value is used. This option does not affect the results for an ARMA(p, q) model where q ≠ 0.

Include sigma-sq in AIC/BIC: When calculating AIC and BIC, as shown in Evaluating the ARMA Model, there is a term k which represents the number of parameters in the model. The usual approach is to include σ as one of the model coefficients, and so k = p + q + 2 for an ARMA(p, q) model with a constant term. For the AR(p) model using OLS regression, however, the σ parameter is not used in calculating AIC and BIC, and so k = p + 0 + 1 for an ARMA(p, 0) model with a constant term. Actually, the σ parameter is not used in the Solver approach described in Calculating ARMA Coefficients using Solver either.

If you check this option and either q > 0 or Make AR(p) agree with OLS is unchecked, then σ is included as a parameter when calculating AIC and BIC; otherwise, it is not.

Reformat for Linear Regression: In the case of a time series that is modeled as an AR(p) process, you can choose to use ordinary linear regression using the Real Statistics Linear Regression data analysis tool. To do this the data in the time series must be reformatted as shown in the following example.

If you check this option then the time series data is reformatted so that it can be sued as input to the Linear Regression tool; otherwise, no such reformatted data is output. In either case, the usual ARIMA calculations are made.

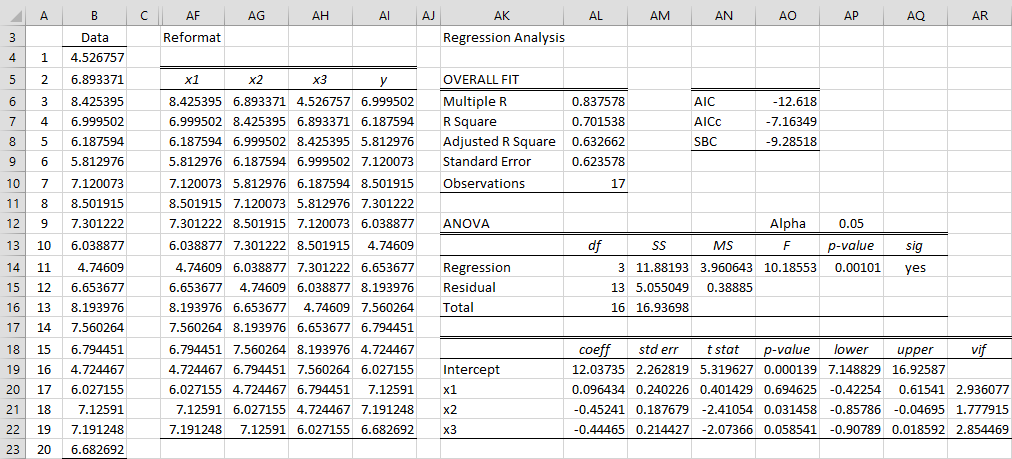
Example 1: Perform multiple linear regression for the AR(3) model of the time series in range B4:B23 of Figure 1.

This time we choose the ARIMA Model and Forecast data analysis tool and insert the range B4:B23 in the Input Range field, insert 3 in the AR order field, 0 in the MA order field and check the Reformat for Linear Regression option.

When we click on the OK button, we see output similar to that in Figures2, 3 and 4 of Calculating ARMA Coefficients using Solver along with the output in columns AF through AI of Figure 1.

Figure 1 – Linear regression for time series data

We can now use the Linear Regression data analysis tool using range AF5:AI22 as input to obtain the linear regression output shown on the right side of Figure 1.

Note that if when we ran the ARIMA Model and Forecast data analysis tool on the data range B4:B23 with 3 in the AR order field and 0 in the MA order field, we had also checked the Constant included in the model, along with the Make AR(p) agree with OLS and Include sigma-sq in AIC/BIC fields, then the output would agree with the linear regression model shown in Figure 1.

Real Statistics Function: The Real Statistics Resource Pack provides the following array function where R1 is an n × 1 column range containing time series data and p is a positive integer

ARMap(R1, p): outputs an n–p × p+1 range which contains X and Y data equivalent to the data in R1 in order to perform multiple linear regression

In fact, the ARIMA Model and Forecast data analysis uses this function to produce the reformatted data range described above. In particular, range AF6:AI22 in Figure 1 contains the array formula =ARMap(B4:B23,3).