Basic Concepts
Sometimes linear regression can be used with relationships that are not inherently linear but can be made to be linear after a transformation. In particular, we consider the following exponential model:
y = αeβx
Taking the natural log (see Exponentials and Logs) of both sides of the equation, we have the following equivalent equation:
ln y = ln α + βx
This equation has the form of a linear regression model (where I have added an error term ε):
y′ = α′ + βx + ε
Observations
Since αeβ(x+1) = αeβx · eβ, we note that an increase in x of 1 unit results in y being multiplied by eβ.
A model of the form ln y = βx + δ is referred to as a log-level regression model. Clearly, any such model can be expressed as an exponential regression model of form y = αeβx by setting α = eδ.
Example
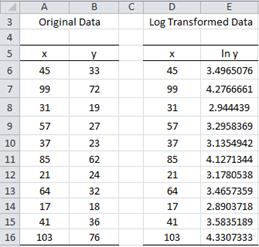
Example 1: Determine whether the data on the left side of Figure 1 fits with an exponential model.
Figure 1 – Data for Example 1 and log transform
The table on the right side of Figure 1 shows ln y (the natural log of y) instead of y. We now use the Regression data analysis tool to model the relationship between ln y and x.
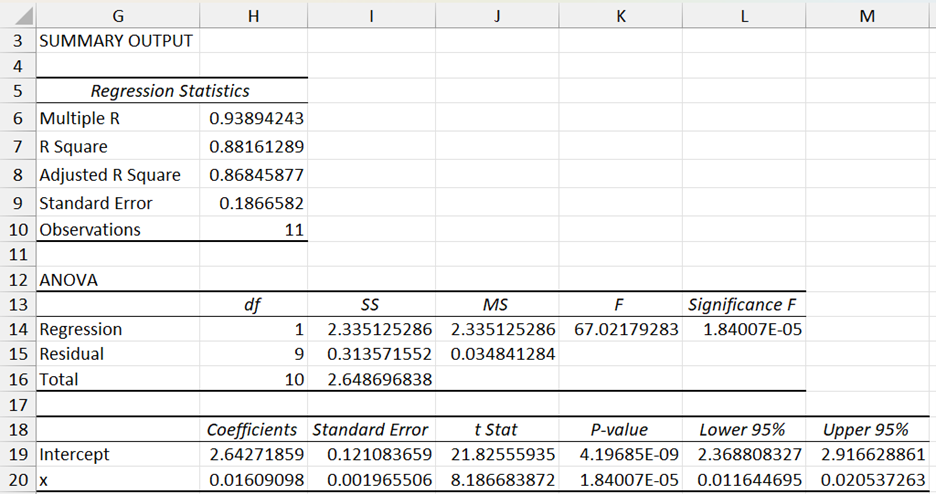
Figure 2 – Regression data analysis for x vs. ln y from Example 1
The table in Figure 2 shows that the model is a good fit and the relationship between ln y and x is given by
ln y = 2.64 + .016x
Applying e to both sides of the equation yields
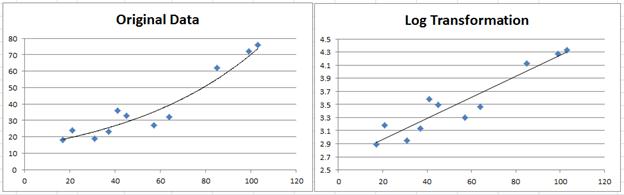
We can also see the relationship between x and y by creating a scatter chart for the original data and choosing Layout > Analysis|Trendline in Excel and then selecting the Exponential Trendline option. We can also create a chart showing the relationship between x and ln y and use Linear Trendline to show the linear regression line (see Figure 3).
Figure 3 – Trend lines for Example 1
As usual, we can use the formula y = 14.05∙(1.016)x described above for prediction. Thus if we want the y value corresponding to x = 26, using the above model we get ŷ =14.05∙(1.016)26 = 21.35.
We can get the same result using Excel’s GROWTH function, as described below.
Worksheet Functions
Excel Functions: Excel supplies two functions for exponential regression, namely GROWTH and LOGEST.
LOGEST Function
This worksheet function is the exponential counterpart to the linear regression function LINEST described in Testing the Slope of the Regression Line. Once again you need to highlight a 5 × 2 area and enter the array function =LOGEST(R1, R2, TRUE, TRUE), where R1 = the array of observed values for y (not ln y) and R2 is the array of observed values for x, and then press Ctrl-Shft-Enter. LOGEST doesn’t supply any labels, and so you will need to enter these manually.
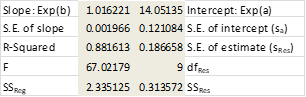
Essentially LOGEST is simply LINEST using the mapping described above for transforming an exponent model into a linear model. For Example 1 the output for LOGEST(B6:B16, A6:A16, TRUE, TRUE) is as in Figure 4.
Figure 4 – LOGEST output for data in Example 1
GROWTH Function
This worksheet function is the exponential counterpart to the linear regression function TREND described in Method of Least Squares. For R1 = the array containing the y values of the observed data and R2 = the array containing the x values of the observed data, GROWTH(R1, R2, x) = EXP(a) * EXP(b)^x where EXP(a) and EXP(b) are as defined from the LOGEST output described above (or alternatively from the Regression data analysis). E.g., based on the data from Example 1, we have:
GROWTH(B6:B16, A6:A16, 26) = 21.35
which is the same result we obtained earlier using the Regression data analysis tool.
GROWTH can also be used to predict more than one value. In this case, GROWTH(R1, R2, R3) is an array function where R1 and R2 are as described above and R3 is an array of x values. The function returns an array of predicted y values for the x values in R3 based on the model determined by the values in R1 and R2.
Observation: Note that GROWTH(R1, R2, R3) = EXP(TREND(R1, R2, LN(R3)))
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Microsoft Support (2012) LOGEST function
https://support.microsoft.com/en-au/office/logest-function-f27462d8-3657-4030-866b-a272c1d18b4b#:~:text=In%20regression%20analysis%2C%20the%20LOGEST,entered%20as%20an%20array%20formula.
Microsoft Support (2012) GROWTH function
https://support.microsoft.com/en-gb/office/growth-function-541a91dc-3d5e-437d-b156-21324e68b80d
Hi, Charles
If you know, could you tell me Excel`s RSQ (R2) command counterpart for exponential regression?
many thanks
Alex,
I don’t think there is an equivalent Excel function for exponential regression.
Depending on how you view exponential regression, you can use the array formula =RSQ(EXP(Y),EXP(X))
Charles
Hi Charles
thanks
Hi Charles! I’m a novice learning about price elasticity. Can you point me to a method for calculating multiple exponential regression? I’m not looking for a model, and I know how to use Excel’s solvers and analysis toolpacks. More than anything I’d like to understand how to calculate it the old-fashioned way. Something that tells me the various parts and how to calculate them. Do you know of anything like this?
Hello Andy,
The approach is very similar to that described for Exponential Regression.
Approach 1: Take the natural log of both sides of the equation and then use ordinary linear regression
Approach 2: Use Solver, exactly as described for Exponential Regression.
Charles
Dear Charles.
Thank you very much for the exponential regression explanation.
I just have 1 question. For the exponential regression equation y= A e^rx , How do we find the value for r for only 2 data points example (0, 1.3964) (1, 1.3423) in excel without plotting a graph.
Chris,
You have two equations in two unknowns:
1.3964 = A e^(0*r)
1.3423 = A e^(1*r)
From the first equation, A = 1.3964. From the second equation
1.3423 = A e^r = 1.3964 e^r. Taking the log of both sides, we get
ln(1.3423) = ln(1.3964) + r
Charles
Hi,
Can the following equation be expressed linearly? if so, how?
y = e^B0 + B1 * X1 + B2 * X2 + E Note: B= Beta
Hello Gerald,
If I understand the equation correctly, this equation is of the form y = B1 * X1 + B2 * X2 + C where C = e^B0 + E is the intercept coefficient. Once C is found, then B0 = ln(C-E)
This can be done by OLS linear regression provided the intercept coefficient takes the correct form.
Charles
Charles,
Great article. I recently came across this so called exponential regression and as you mentioned it is a linear regression after some transformation. So the question arises that one needs to check all the appropriate assumptions for linear regression before applying this excel function, right? In addition, if the data is a time series then one needs to check for stationarity as well. Please let me know if you agree or not
Hello Bilal,
Glad you found the article useful.
1. This depends on how you will be using exponential regression. Most of the assumptions are related to confidence intervals for the regression parameters. If you are just using the regression model for predicting then you don’t need to meet all the linear regression assumptions.
2. For time series data, the key issue is autocorrelation, not stationarity. If there is autocorrelation, you need to correct for this. This is described on the Real Statistics website.
Charles
Hi Charles.
How can I draw the 95% CI for the exponential regression line?
I have X= time
Y is the survival function
1. You can calculate the lower and upper interval for each point in linear regression as described at
https://real-statistics.com/regression/confidence-and-prediction-intervals/
You can use this to create three graphs on the same chart (lower and upper points as well as data points). You can then add a linear trendline for the data points. The result should look something like that in Figure 1 of the above webpage.
2. Since exponential regression using a linear model is really linear regression with a transformation, you need to perform the above steps, but before plotting the results you need to use the inverse transformation.
3. I will add an example of how to do this in the next release of the Real Statistics software.
I need to fit my data with an exponential function y=A*(1-exp(-x/B)). How to linearize my data, apply the linear fit, and find the coefficients A and B?
Hi Lexy,
I don’t believe that you can linearize this equation if A and B are regression coefficients.
If A and B are known constants then it would be possible to linearize this equation.
Charles
Can i get hand solution for polynomial and exponential solution
Kalpana,
I am not sure about what you mean by “hand solution”. In any case, you can download Excel worksheets about the polynomial and exponential solutions. These can be found at
Example Workbooks
In particular, you should download the Regression 1 workbook.
Charles
Please, can you explain your “error term” to a greater extent?
Jose,
The error term is explained in the Linear Regression portion of the website. See, for example
https://real-statistics.com/regression/regression-analysis/
Charles
Hi Charles,
Thank you for this post. Would you mind elaborating on the process to use if we suspect that a polynomial equation is more appropriate?
What is a good and easy way to make that decision (without diving into the complexities of Model Selection), and how would we then proceed to actually implement it?
Thank you.
Harvey,
I don’t know of a good way to decide on whether a polynomial equation is more appropriate, except by trying it and see how well it predicts the output based on real data. See the following webpage for more info on this topic:
Polynomial Regression
Charles
Y=a*exp(Bx^0.5 + CX^3)
can any one solve this example???
i cant fit into Y= mX + c
Please
Y=aexp(bx^0.5 + cX^3)
can any one solve this example???
i cant fit into Y= mX + c
George,
Take the log of both sides to get ln(Y) = ln(a) + bx^.5 + cX^3. Let y = ln(Y), x1 = X^.5, x2 = X^3, d = ln(a). Thus the equation takes the form
y = b*x1 + c*x2 + d. This of the form of a multiple regression.
Charles
Thanks Charles
Y=β/(1+Aexp^X) pls how do i convert this to linear form
Psalmseen,
y = b/(1+ae^x) is equivalent to 1+ae^x = b/y which is equivalent to b/y – 1 = ae^x. Taking the log of both side yields ln(b/y-1) = x + ln(a).
Unfortunately, this isn’t in the form y = cx + d (unless b is a known constant), and so you need to use some form of non-linear regression (e.g. using Solver).
Charles
tanks
Hi!
Have a question on Exponential trend method, when calculating the U value is it always X-3?
What is the U value?
Charles
Hi,
In linear regression, we set up the null hypothesis as slope (β=0) v’s (β≠0). How can we setup the null hypothesis in exponential regression equation.
Gowher,
It really depends on which parameter you want to test, but the test that corresponds to the one you listed for linear regression is the same in exponential regression, namely (β=0) v’s (β≠0).
Charles
Thanks, if we apply t-test we take degrees of freedom as (n-1) but if we set up the null hypothesis (β=0, i.e slope is equal to zero) v’s (β≠0, i.e, the slope is not equal to zero) in linear regression. Why we have to take degrees of freedom as (n-2)? Please explain.
Gowher,
The degrees of freedom in each case is n-p where p = the number of independent variable. In the first case p = 1 and in the second case p = 2.
Charles
Thanks
sir I have used the above exponential regression model explained by you in which “y” represents total fertility rate(dependent variable) and “x” represents birth order(independent variable) and estimates of TFR have been obtained. Now please tell me how can I check the validity of the model?
Gowher,
The exponential regression model presupposes that this model is valid for your situation (based on theory or past experience). You can use the model to gain evidence that that the model is valid by seeing whether the predictions obtained match with data for which you already know the correct values. E.g. suppose you have a sample of size 100. One approach is to use 80 elements from the sample (taken at random) to create the regression model. Now use this regression model to “predict” the values of the dependent variable in the 20 remaining sample elements. Since you know the correct value of the dependent variable for these 20 items, you can compare the model’s predictions with the correct values to see how well the model performs.
Charles
hello guys ,i want to regress a given data points of t and y ,then find the coefficients and constants for the following models .
y=a*exp(bt^c)
y=a*exp((bt)^c)
can any one help me how to find the a,b and c values by regression for a given datas of experiment of t and y?
Mitku,
If we take the log of both sides of the first equation we get ln y = ln a + bt^c. Now let y’ = ln y, a’ = ln a and x = t^c, then the equation takes the form
y’ = bx + a’. You can then use ordinary regression to find the values for a’ and b. Then a = exp(a’). The only problem with this approach is that c is treated as a constant. If you want to calculate a value for c, then this approach won’t work and you will need to use a non-linear regression approach, e.g. using Solver as I have shown on the website for exponential regression. The situation is similar for the second equation.
Charles
Let’s say we have y = a exp(b*x) + e1 where e1 is the error term. Then we solve ln y = lna + b ln x + e2 where e2 is the error term using the regression. What is the relationship between e1 and e2 so that linearization is accurate?
Mallika,
e2 = ln(a*exp(b*x)+e1) – (lna + b*lnx)
Charles
hi will i able to use this exponential equation for forecasting?
Yes
Is there any Example or link for that. i want manual calculation
Vinodh,
This webpage shows how to transform an exponential regression model into a linear regression model. The webpage uses Excel’s Regression data analysis tool to carry out the regression. If you want to do this part manually, then please see the following webpage:
https://real-statistics.com/regression/least-squares-method/
Charles
Hello, I am new in the field of statistics, I would like to ask how to calculate the growth rate with time series data.I wanna know the crop yield growth rate and calculate the instability in growth.
I have this exponential equation:
Y=ab^t
Where Y=yield
a=constant
b=trend
t=time(from 2000to 2014)
I have the data of crop Yield for this period.
The formula for instability index :CV*(1-R squared)square root
Thanks, waiting your kind reply
Tina,
Have you tried to apply the approach on the referenced webpage?
Charles
@Charles, Yes,I have tried many in this way:
1)calculate ln y
2)regress ln y x
3) calculate exp(b)
When I calculate the Compound Annual Growth rate from the value
of b obtained(CAGR=(antilog b-1 )*100,i find the answer different when i use the common formula to calculate CAGR in excel.
@Charles, can you refer where i can find how to calculate Compound Annual Growth rate with empirical study(not the common formula in excel )
Thanks
Tina,
If all your data lies on the regression line then the CAGR should agree with the usual value. If not, then you could expect the CAGR not to be the same as that generated by the usual formula, although if the data lies close to the regression line, then the results should be similar.
Charles
Hi,
I am in a bit puzzled by following question. I need linear regression to model the following form: y = Ae^(-0.3t); as you can see that b is already known in this case. So, how to do this kind of regression in excel. Actually, I want to compare results with my hand calculations. I have done hand calculations using two methods:
1. without data transformation
2. with data transformation
Now, using these two approaches, I get slightly different values for A. The value for A obtained by using model without data transformation gives a smaller sum of squared errors, as compared to using model with data transformation. I am puzzled by this variation as my understanding is that both systems should give same answers. Is my understanding correct? Am I missing something?
This probably depends on the nature of the data transformation. There is no reason to assume that you will get the same answer from options 1 and 2.
Charles
Thanks, for the clarification. Can you please also guide some source where we can learn about scaled residuls.
Thanks,
Zulfiqar
Zulfiqar,
Here are some references:
https://real-statistics.com/multiple-regression/residuals/
https://support.sas.com/documentation/cdl/en/statug/63347/HTML/default/viewer.htm#statug_intromod_a0000000355.htm
Charles
Can you provide any real life example of log-linear model??
Examples can be found in Howell’s textbook (see Bibliography). Other real examples can be found in various textbooks and online.
Charles
Q. what is the suitable statistical method to calculate and measure the time once we knew the value of y at t0 and value of y at tn ?
In the graph below
y
t
t0 tn
tn-t0=?
Q. what is the suitable statistical method to calculate and measure the time once we knew the value of y at t0 and value of y at tn ?
I think we calculate the time using linear interpolation and certain numerical methods.
In this case, I need to know the statistical method to estimate the time. And how?
We can rewrite the question as follows:
How long time the process takes from initial value y0 to end value yn ?
Yousif,
Sorry, but I don’t understand your question.
Charles
Hi,
Does anyone know if there is a way to calculate the whole thing by hand? The whole formula?
Alan,
The referenced webpage tells you how to perform exponential regression based on linear regression. If you look at the webpages on linear regression as well, you will see how to perform linear regression (and therefore exponential regression) by hand. This will not consist of a single formula.
Charles
Hi,
What do you suppose is the simplest way in which I could show and explain how the method of obtaining an exponential function via a linear model is valid to all exponential functions?
I have already demonstrated that an exponential function (ab^x) can be found by first obtaining a linear function using using logs and graphing however need to further prove that it can be applied to all exponential functions.
Would the use of natural log be useful for the (ae^kx)? If so how would I go about showing this with a given set of data? My first and second x and y values are (0,100) and (1,62).
Brittany,
Yes, the same technique should apply. y = ae^(kx) means that lny = lna + kx.
Charles
I have further question after finding the intercepts.
Using Y=a.exp(kt)
In order to determine the value of t for given max/min value of Y (max = 100, min = 0 in my application.) wouldn’t the value of t be Inf. ?
By subsitution, t = (ln(Y)-ln(a) )/ k
Also , When the logarithmic distance between the 2 points to determine the constants is ‘more’ or ‘less’ , how would be the prediction of t ?
Your comments would be useful. Thanks
Pranav,
Since t = (ln(Y)-ln(a))/ k, t would be undefined when y = 0, but would have a finite value when y = 100.
Sorry, but I don’t understand your other question.
Charles
Sorry about not posing the question clearly.
If we had to calculate the value of t at end positions(ex:1 and 100),
how would the separation between the 2 points used to determine the values of a and k affect the value of t.
Pranav,
Sorry, but I still don’t understand the question.
Charles
Hi Charles,
How to determine the vlaues of a and b without using excel functions ( on paper)
Thanks
Can linear model intepretation of slope and intercept be applied directly after take the natural log ?
Pranav,
Yes, as described on the referenced webpage.
Charles
Pranav,
See the following webpage for the calculation of a and b (for the linear case) by hand.
https://real-statistics.com/regression/least-squares-method/
Charles
Very detailed information. Thanks for the link.
thanks for the post
Y=αe^-βt
can any one solve this example???
i can fit into Y= α+βt
but answer … EInY=-0.37182, E(InI)^2=3.45846, EtInI=-1.37554
NOTE E MEANS SUM
thanks for the wonderful post; please check out this question how do you solve this
Y=aBexp-kt
please find the transformation
Dennis,
If y = aexp(-kx), then lny = -kx + lna, which takes the form of a linear regression y’ = -kx + a’ where y’ = lny and a’ = lna.
Charles
Hello,
Can you please explain to me how you would do the regression data analysis…? I want to know how to get the values in figure 2, Thank you!
Lily,
See the webpage
https://real-statistics.com/regression/hypothesis-testing-significance-regression-line-slope/
Charles
Hi,
Can you please elaborate, if we have an exponentially decaying function, when we need to/ we can use linear fiitting for interpolation instaed of using exponentially decaying curve?
Nazia,
As described on the referenced webpage, you can always model data that fits an exponential function using a linear model. The non-linear model (as described on the Real Statistics website) will be a little more accurate.
Charles
Hi,
I saw in some papers that the coefficients are interpreted as semi-elasticity without outlining the initial model. Does that mean that the model is in log-level form ?
Ahmed,
Yes. This is explained on the following webpage>
Power Regression
Charles
When we use other functional forms to run the regression analysis, why do we then choose the functional form with the least MS residual to analyse the result?
Zaynab,
I don’t see any reference to least MS residual on the referenced webpage. In general, the logic behind minimizing the squared error is as described on the webpage
Maximum Likelihood Function.
Charles
Under what circumstances would it be appropriate to log transform only the independent variable for an exponential regression?
Would that be considered a log-level or a different type?
Rachel,
This transformation is appropriate when it provides a better fit for your data.
This is level-log regression as described on the webpage https://real-statistics.com/regression/power-regression/.
Charles
Thanks Charles. These pages are very helpful.
However, a power regression includes the transformation of both the x and y axis.
log-log: power
log-level: exponential
What is it called when you just transform the independent variable?
Rachel,
See Power Regression
Charles
thank you, i will try to understand this stuff. I actually a bit confused. 🙁
Dear Charles
I am trying to download the software or application as per your posting from https://real-statistics.com/free-download/real-statistics-resource-pack/#install
It might be possible that I am not doing it properly, because I still can not download it to my computer and have it as an Add in tool
Could you please help me out with some step by step guidance ?
Thanks
MK
Moshe,
To download the software, just go to the following webpage and click on the Free Download button (assuming that you are using Excel 2010, 2013 or 2016 for Windows)
Real Statistics Resource Pack
To install the software after you have downloaded it, perform the following steps:
1. Open Excel, but don’t try to open the realstats.xlam file that you downloaded
2. Press Alt-TI (i.e. hold the Alt key down and simultaneously press T followed by I)
3. On the Add-Ins dialog box that appears press the Browse button and locate where you stored the realstats.xlam file that you downloaded (this done in a similar manner as when you Open a file)
4. Once you have done this, make sure that the Realstats option on the Add-Ins dialog box is checked and click the OK button
Please reply soon… i need it
What if we take log to the base 10 i.e. normal log instead of ln i.e. natural log?
Will the answers differ?
You can use log base 10 instead of the natural log, but the answers will differ by a constant factor since LN(x) = a Log(x) for any x where a = 2.302585…
Charles
Y=aexp^(-x/b)
can any one solve this equation?
Take the natural log of both sides of the equation and then use properties of logs and exp:
ln y = ln(a exp^(-x/b))
ln y = ln a + ln(exp^(-x/b))
ln y = ln a – x/b
x/b = ln a – ln y
x = b ln (a/y)
Charles
In order to run the regression why don’t you have to take the natural log form of both x and y before coming up with the equation? Then once you have it in the natural log form would you just take the equation and set it equal to marginal cost to find the profit maximizing quantity? Thank you.
Alyssa,
I have taken the natural log of both sides of the equation. Remember that LN(EXP(x)) is x.
Regarding “…marginal cost to find the profit maximizing quantity”, you apparently have a particular application of exponential regression in mind, but exponential regression can be used to address a variety of applications, not just those from economics.
Charles
how all functions (linear, semi log, double log and exponential) can be applied
Sorry, but I am not sure that I understand your question, although perhaps the following webpage provides the information you are looking for.
Power Regression
Charles
Pls I need a solution to this problem where can I get semi-log regression and double log regression in SPSS or which software can I use to solve it
Sorry, but I am not that familiar with SPSS. I do my statistical analysis using Excel and my software, the Real Statistics Resource Pack.
Charles
Can you provide any real life example of log-linear model??
Taniya,
Take any example you have for the chi-square test for independence (of two variables) and simply add another variable. Log-linear models analyze the resulting 3-way contingency tables.
Charles
I would like to know about decline curves and rates.
y = 2E+21e-0.002x
I want to know decline rate is -0.02%? My problems are to know rates and -0.002.
.002 is the exponential decay constant, which results in a decline rate of .2%.
If this is not the answer to your question, please explain better.
Charles
Exactly how do you arrive at your residual values? Can you please explicitly show us the calculation? As an example, the residual between the observed value x of 7.4 and the observed value y of 5.2.
If you are modelling y = a*e^(bx), then the linear model is lny = bx + lna. The residual of the linear model is the difference between the observed value of lny and the predicted value of lny. For the model in Example 1 of the referenced webpage, when x = 7.4 then the model predicts y to to be 15.828 (although caution should be used since the value for x is a bit output the observed data range). Since you said that the observed value of y is 5.2, the observed value of ln y is ln 5.2 = 2.001 and the predicted value of ln y is ln 15.828 = 2.762, and so the residual is 2.001 – 2.762 = 0.761.
Technically the residual for the exponential model is simply 5.2 – 15.828 = -10.628, although the value in the above paragraph may be more relevant for many purposes.
Charles
Y=αxe^βx
can any one solve this example???
i cant fit into Y= mX + C
By “solve” do you mean put y=αxe^βx into the form Y = mX + C? This doesn’t seem likely since logy = βx + logα + logx takes the form Y = mX + logX + C.
Charles
Hey, I have a doubt. If we have a data and we need to find the relation between them,we use correl to see if they have any linear relation between them. Likewise is there any counterpart for correl to see the exponential relation between the data. If we have a data,how can we come to a conclusion that they are exponentially related and then use logest or growth to predict the further values.please help me
Petr,
As described on the referenced webpage, if x and y have a exponential relationship, i.e. y = abe^x, then ln y = bx + ln a, which is a lineaar relationship. Thus you could use correl between ln y and x to test whether x and y have an exponential relationship.
Charles
wise contributions from all of you guys, my problem has been solved. thank you
For exponential, logarithmic and power trend fits, Excel uses the least square method on the data pairs [x, ln(y)] (in the exponential case).
From this approach inherit two issues:
1) The R-squared given in charts is the one of the linear fit to those [x, ln(y)] pairs. NOT the R-squared of your original data! So do not rely on this value in the chart!
This fact is documented somewhere in Excel … not too easy to find though.
2) The overall approach will in general NOT deliver an optimal fit!!! I can provide examples, where the Excel trend (no matter if calculated as a chart trendline or by a worksheet function like GROWTH) is worse than an exponential fit calculated e.g. with an Levenberg-Marquardt algorithm.
This fact is NOT documented in Excel – maybe not even known to Microsoft.
On the contrary, Excel documentation states that its trends are “best fit”. They are not – always.
So, if you want to be sure whether your data follow an exponential, logarithmic or power pattern: do not rely on Excel!
Jorj,
Sorry that I haven’t responded to your comment earlier, but I have been on vacation for the past few weeks. I appreciate your serious comment and plan to look into it. Based on your comments I may need to provide a new version of the referenced regression algorithms that provide a better fit along the lines that you have suggested.
Charles
Hi Charles.
I just came across this thread and if you have already addressed this issue elsewhere, just ignore my post.
We can view the exponential model as follows. Y has a log-normal distribution while Ln(Y) has a normal distribution. The relationship between the Normal and Log-normal distribution is well defined. For instance, if the variable Ln(Y) has a Normal distribution with mean = mu and standard deviation = sigma, then the variable Y has Log-normal distribution (with parameters mu and sigma). The mean of Y is given by e^(mu + 0.5*Sigma^2). It is NOT e^(mu). Similarly higher order moments can be defined (see Wikipedia Log-normal).
The following notation is not exactly right, but I hope it conveys the message. Excel predicted values are off because of the fact that Excel trend line does prediction as e^(bo + b1X) (where b0 and b1 are the result of regressing Ln(Y) on X). But e^(bo + b1X) is not the expected value of Y given X. The correct expression for the expected value of Y given X should be e^(b0 + b1X + 0.5*MSE). So Excel will consistently under-estimate the expected value of Y given X (unless it is a perfect fit in which case MSE will be 0).
This would be the solution for the Exponential model, but not necessarily for the other models. So Jorj is correct in that the Excel may not be the best approach for non-linear estimation. Most people assume that transformations are easy … they usually are not. And this is a case in point.
Krish,
Thanks for your comments. I had been reluctant to spend the time necessary to implement the Levenberg-Marquardt algorithm as suggested by Jorj, but I can see that it is not sufficient to simply accept the approach used by Excel. Shortly I will modify the website to at least comment on the discrepancy and try to come up with a compromise solution.
Charles
Krish,
The latest release of the software, Release 3.8, provides a nonlinear regression solution to the exponential model.
Charles
correction:
I meant to say
Is it correct to say that if x increases by delta_x units, y increases by 100*(eˆ(b1*delta_x)-1)%? (for b1 much larger that 0.1)
Hi,
Yes this is correct. I believe this is true for any value of b1, not just for b1 much larger than 0.1, using simple algebra.
Charles