Maximizing the log-likelihood statistic
Property 1: The maximum of the log-likelihood statistic occurs when
Proof: Let
where the yi are considered constants from the sample and the pi are defined as follows:
Here![]()
which is the odds ratio (see Definition 3 of Basic Concepts of Logistic Regression). Now let
To make our notation simpler we will define xi0 = 1 for all i, and so we have
Thus
Also, note that
The maximum value of ln L occurs where the partial derivatives are equal to 0. We first note that
Thus
The maximum of ln L occurs when
for all j, completing the proof.
Newton’s method for logistic regression
To find the values of the coefficients bi we need to solve the equations of Property 1.
We do this iteratively using Newton’s method (see Definition 2 and Property 2 of Newton’s Method), as described in the following property.
Property 2: Let B = [bj] be the (k+1) × 1 column vector of logistic regression coefficients, let Y = [yi] be the n × 1 column vector of observed outcomes of the dependent variable, let X be the n × (k+1) design matrix, let P = [pi] be the n × 1 column vector of predicted values of success and V = [vi] be the n × n matrix where vi = pi(1–pi). Then if B0 is an initial guess of B and for all m we define the following iteration
then for m sufficiently large, Bm+1 ≈ Bm, and so Bm is a reasonable estimate of the coefficient vector.
Proof: Define
where xi0 = 1. We now calculate the partial derivatives of the fj.
Let vi = pi(1–pi) and using the terminology of Definition 2 of Newton’s Method, define
Now
where X is the design matrix (see Definition 3 of Multiple Regression Least Squares), Y is the column matrix with elements yi and P is the column matrix with elements pi. Let V = the diagonal matrix with the elements vi on the main diagonal. Then
We can now use Newton’s method to find B, namely define the k × 1 column vectors Pm and Bm and the (k+1) × (k+1) square matrices Vm and Jm as follows based on the values of P, F, V, and J described above.
Then for sufficiently large m, F(Bm) = 0, which is equivalent to the statement of the property.
Reference
Shalizi, C. (2009) Logistic regression and Newton’s method. Data mining class
https://www.stat.cmu.edu/~cshalizi/350/lectures/26/lecture-26.pdf
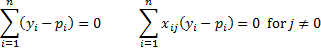
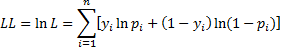
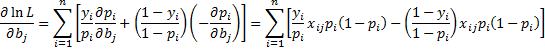
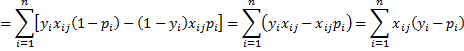
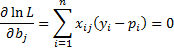
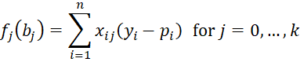
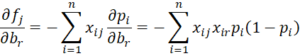
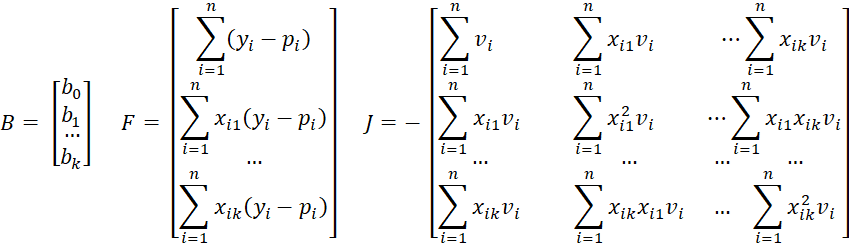
In your proof of Property 2, is there a reason you reversed the position of y and p in the (p-y)–rather than (y-p)–expression? Secondly, there appears to be a missing (second) “=” in the df/db partial expression that you show in the proof of Property 2.
Hello Ed,
Thanks for pointing out the errors and inconsistencies on this webpage.
I just updated this webpage. I did it very quickly, and so hopefully, I haven’t made a mistake.
Charles
Hello, i want ask you about how to find initial for Beta (Bm)? thank you.
You can use almost any values for the initial guess. The default will be all zeros.
Charles
Hi,
Is F= XT (Y-P) instead of XT(Y-mu)?
Regards,
Ashoka
Hello Ashoka,
Yes, you are correct. Thank you for identifying this error. I have now corrected this on the website.
Charles
Hello
in your sentence : ” We can now use Newton’s method to find B, namely define the k × 1 column vectors Pm and Bm and the (k+1) × (k+1) square matrices Vm and Jm as follows based on the values of P, F, V and J described above.”, the Vm matrix should be of size (n,n)?
Thierry,
Yes, you can view V is an n x n diagonal matrix.
Charles
Charles,
I would like to bring your attention on the following three points in the Property 1 proof:
1. Exp(-b0-sum(bjxij)) should be (1-pi)/pi instead of pi/(1-pi).
2. Exp(zi) should also be (1-pi)/pi instead of pi/(1-pi).
3. For the last sentence of the proof, “ln L” is missing between “The maximum of” and “occurs”.
-Sun
Hi Sun,
Thanks for finding these errors. I have now corrected all three items.
Charles