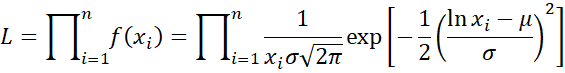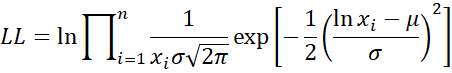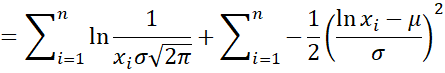We now provide more detail about the LL for a log-normal distribution and the estimation of the μ and σ parameters using MLE (see Fitting Lognormal Parameters via MLE).
LL formulas
The log-likelihood function takes the form
Thus, the log-likelihood function takes the form
Thus
Parameter estimation
Using calculus, LL is maximized when the two partial derivatives are zero.
which implies that
Since
It now follows that
References
Genos, B. F. (2009) Parameter estimation for the Lognormal distribution
https://scholarsarchive.byu.edu/cgi/viewcontent.cgi?article=2927&context=etd
Wikipedia (2020) Log-normal distribution
https://en.wikipedia.org/wiki/Log-normal_distribution
Pavlovic, M. (2022) Formulas & proofs for the log-normal distribution
https://majapavlo.github.io/blog/2022/02/02/lognorm_formulas.html