Basic Concepts
We present the original approach to performing the Shapiro-Wilk Test. This approach is limited to samples between 3 and 50 elements. By clicking here you can also review a revised approach using the algorithm of J. P. Royston which can handle samples with up to 5,000 (or even more).
The basic approach used in the Shapiro-Wilk (SW) test for normality is as follows:
- Arrange the data in ascending order so that x1 ≤ … ≤ xn.
- Calculate SS as follows:
- If n is even, let m = n/2, while if n is odd let m = (n–1)/2
- Calculate b as follows, taking the ai weights from Table 1 (based on the value of n) in the Shapiro-Wilk Tables. Note that if n is odd, the median data value is not used in the calculation of b.
- Calculate the test statistic W = b2 ⁄ SS
- Find the value in Table 2 of the Shapiro-Wilk Tables (for a given value of n) that is closest to W, interpolating if necessary. This is the p-value for the test.
For example, suppose W = .975 and n = 10. Based on Table 2 of the Shapiro-Wilk Tables the p-value for the test is somewhere between .90 (W = .972) and .95 (W = .978). You can estimate this p-value using interpolation (see Interpolation).
Examples
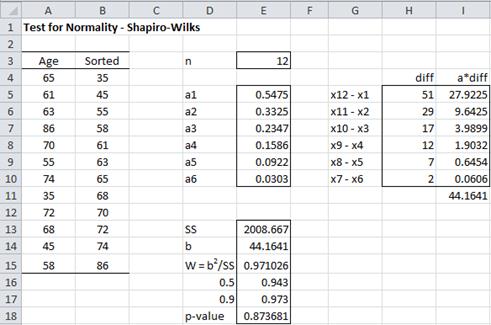
Example 1: A random sample of 12 people is taken from a large population. The ages of the people in the sample are shown in column A of the worksheet in Figure 1. Is this data normally distributed?
Figure 1 – Shapiro-Wilk test for Example 1
We begin by sorting the data in column A using Data > Sort & Filter|Sort (see Sorting and Filtering) or the Real Statistics QSORT function (see Sorting and Removing Duplicates), putting the results in column B. We next look up the coefficient values for n = 12 (the sample size) in Table 1 of the Shapiro-Wilk Tables, putting these values in column E.
Corresponding to each of these 6 coefficients a1,…,a6, we calculate the values x12 – x1, …, x7 – x6, where xi is the ith data element in sorted order. E.g. since x1 = 35 and x12 = 86, we place the difference 86 – 35 = 51 in cell H5 (the same row as the cell containing coefficient a1). Column I contains the product of the coefficients and difference values. E.g. cell I5 contains the formula =E5*H5. The sum of these values is b = 44.1641, which is found in cell I11 (and again in cell E14).
We next calculate SS as DEVSQ(B4:B15) = 2008.667 (cell E13). Thus W = b2 ⁄ SS = 44.1641^2/2008.667 = .971026 (cell E15).
p-value using interpolation
We now look for .971026 when n = 12 in Table 2 of the Shapiro-Wilk Tables and find that the p-value lies between .50 and .90. The W value for .5 is .943 and the W value for .9 is .973.
Interpolating .971026 between these values (using linear interpolation), we arrive at p-value = .873681. Since p-value = .87 > .05 = α, we retain the null hypothesis that the data are normally distributed. Since this p-value is based on linear interpolation, it is not very accurate, but the important thing is that it is much higher than the alpha value, and so we can retain the null hypothesis that the data is normally distributed.
Comparison with other tests
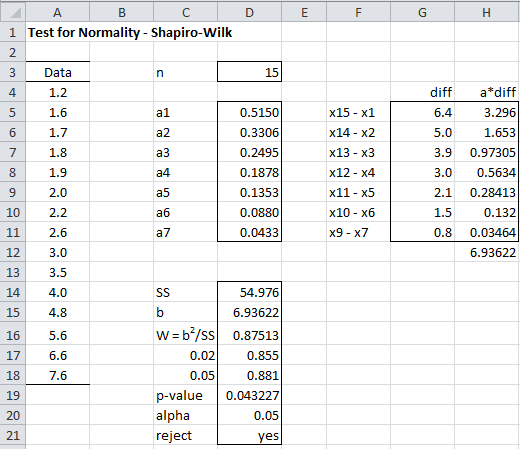
Example 2: Using the SW test, determine whether the data in Example 1 of Graphical Tests for Normality and Symmetry (repeated in column A of Figure 2) are normally distributed.
Figure 2 – Shapiro-Wilk test for Example 2
As we can see from the analysis in Figure 2, p-value = .0432 < .05 = α, and so we reject the null hypothesis and conclude with 95% confidence that the data are not normally distributed, which is quite different from the results using the KS test that we found in Example 2 of Kolmogorov-Smironov Test, but consistent with the QQ plot shown in Figure 5 of that webpage.
Real Statistics Support
Real Statistics Function: The Real Statistics Resource Pack contains the following functions.
SHAPIRO(R1, FALSE) = the Shapiro-Wilk test statistic W for the data in R1
SWTEST(R1, FALSE, interp) = p-value of the Shapiro-Wilk test on the data in R1
SWCoeff(n, j, FALSE) = the jth coefficient for samples of size n
SWCoeff(R1, C1, FALSE) = the coefficient corresponding to cell C1 within sorted range R1
SWPROB(n, W, FALSE, interp) = p-value of the Shapiro-Wilk test for a sample of size n for test statistic W
The functions SHAPIRO and SWTEST ignore all empty and non-numeric cells. The range R1 in SWCoeff(R1, C1, FALSE) should not contain any empty or non-numeric cells.
When performing the table lookup, the default is to use the recommended type of interpolation (interp = TRUE). To use linear interpolation, set interp to FALSE. See Interpolation for details.
For Example 1 of Chi-square Test for Normality, SHAPIRO(A4:A15, FALSE) = .874 and SWTEST(A4:A15, FALSE, FALSE) = SWPROB(15,.874,FALSE,FALSE) = .0419 (referring to the worksheet in Figure 2 of Chi-square Test for Normality).
Note that SHAPIRO(R1, TRUE), SWTEST(R1, TRUE), SWCoeff(n, j, TRUE), SWCoeff(R1, C1, TRUE), and SWPROB(n, W, TRUE) refer to the results using the Royston algorithm, as described in Shapiro-Wilk Expanded Test.
For compatibility with the Royston version of SWCoeff, when j ≤ n/2 then SWCoeff(n, j, FALSE) = the negative of the value of the jth coefficient for samples of size n found in the Shapiro-Wilk Tables. When j = (n+1)/2, SWCoeff(n, j, FALSE) = 0 and when j > (n+1)/2, SWCoeff(n, j, FALSE) = -SWCoeff(n, n–j+1, FALSE).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Shapiro, S.S. & Wilk, M.B. (1965) An analysis of variance for normality (complete samples). Biometrika, Vol. 52, No. 3/4.
Hi Charles,
I am doing a dissertation and have run outlier tests and histograms at a 90% confidence level, should my shapiro-wilk test also at 90% confidence level or the usual 95%?
Thank you
Usually, you use 95% for both tests. If you choose 90% then make sure that you state this clearly in your thesis.
Charles
Hello Charles,
When performing the SW test with the data from example 1 and 2 with SPSS the results of p-value do not match, what could be the difference?
Oscar,
Perhaps SPSS is using the Royston version of the test. This is described at
https://www.real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/shapiro-wilk-expanded-test/
Charles
Hello what is real meaning of W and p value
W is just a statistic that is useful in calculating the p-value. To gain more insight, you will need to read the original paper from Shapiro and Wilk. See Bibliography
See the following for a definition of the p-value:
Hypothesis Testing
Charles
A question Mr. Charles …
Which interpolation method ( https://www.real-statistics.com/statistics-tables/interpolation/ ) you recommend to use in Table 2 of SW original method ( https://www.real-statistics.com/statistics-tables/shapiro-wilk-table/ ) ?
Thanks a lot!
Hello Jesus,
I believe that I am using log interpolation, but it is better to use the Royston version of the SW test and avoid the whole issue of interpolation.
Charles
thanks and regards! …
Thank you very much Charles. I follow your examples for Excel in WPS Spreadsheet and the results are fine. One question, do you write some paper about this?
Thank you…
Cleonir,
Thank you for your kind remarks.
I have had the intention to write a book about this and other statistics subjects but supporting this website and the Real Statistics software tends to take up the spare time that I have.
Charles
Hi Charles,
Thank you for the great work you are doing.
I am dealing with a set of data that has failed the Shapiro-Wilk’s test for normality (ie. the p-value is less than 0.05). I transformed the data by evaluating its natural logarithms and conducted the Shapiro-Wilk’s test on it. (hoping that the data would be lognormal). It still fails this test for log normality. According to the literature, such data sets should be lognormally distributed. What other statistical tests can I use to test whether my data is lognormal?
Thank you in anticipation
Hello Newman,
I assume that you found that the set of ln(x) where x is in your original sample was not normally distributed per the Shapiro-Wilk test. Unless there are a lot of ties, this tends to be the best test for normality. You could try the Anderson-Darling test, but if the original data is truly lognormally distributed, then the SW test should confirm this. What is the p-value of the test?
Charles
Hi,
With the example data (65,61,63,86,70,55,74,35,72,68,45,58) I get the following p-value from both R and a python function, 0.9216, as opposed to the 0.873681129
you get. I can reproduce your value of 0.873681129
in spreadsheet calculations. Do you have any idea why there’s a discrepancy, please?
Thanks,
James. Picksley
Hello James,
They are using the Royston version of the Shapiro-Wilk test. This is also the default version in Real Statistics. If the data is in range A1:A12, then SWTEST(A1:A12) = .9216, while SWTEST(A1:A12,FALSE) = .8737. The problem with the calculation in the original version of the SW test is that the interpolation that is being used is probably not so accurate.
Charles
Hi Charles,
Thanks for the reply. I’d just worked it out and then came here to see you’d put a response up! I spotted it because I have a set of data where W in the original test is outside of the range of table 2, so I wasn’t getting a valid result, so I ran it through the extended version and got a match with R and python.
Sorry to have wasted your time. Thanks very much for this website. I’ve found it very useful over the last few years.
Cheers,
James.
James,
No problem. Glad that I could clarify things.
Charles
Primeramente saludar a Charles por su publicacion desde aqui de Bolivia. por muchos años no podia hacer correr los datos con mas de 50 muestras prueba Sapiro Willk. ahora si se puede con esta prueba ampliada. Pues llege a desifrar todas las formulas. Solo que tengo una observacion. Al final, la hipotesis de normalidad con la distribucion de probabilidad normal esta confuso con la prueba original dice no y con el ampliado dice si del ejemplo con 12 muestras. deberian coicidir ambos, en este caso la normalidad de esos datos se aceptaria o tal ves estoy equivocado. Yo acostubro trabajar al 5% de nivel de significancia y no asi con nivel de confianza que es al 95%. ya que la misma prueba te aroja a nivel de significancia. En este caso mi sale 0,078 redondeado, pero se resto de 1, seria a nivel de confianza que deberia contrastarse. Tal vez estoy muy grosero, pero muchas gracias por su aporte.
Hello Ruben,
Thank you for your kind remarks.
Both the original and expanded versions of the Shapiro-Wilk test should give similar results. If the p-value < alpha then you have evidence that the data does not come from a normally distributed population. Charles
Charles, Can Shapiro-Wilk (SW) be used on datasets that have tied values? The State has directed me to use SW for groundwater monitoring data, and there are often tied values in groundwater data. I’ve been told there is additional data manipulation that must be done to use SW on data with tied values. I am hoping you can tell me what these additional manipulations are. Here’s an example data set: 0.075, 0.077, 0.1, 0.1, 0.1, 0.15, 0.19, 0.2, 0.2, 0.23, 0.27, 0.28, 0.28, 0.29, 0.3, 0.33, 0.34, 0.35, 0.37, 0.37, 0.44, 0.52, 0.56, 0.58. I use excel to calculate W and get W=0.9437 (without accounting for ties).
Thank you.
Hello David,
There is a method for correcting ties in the SW test, but I am not familiar with it. The following paper describes the process:
https://www.tandfonline.com/doi/abs/10.1080/00949658908811146?journalCode=gscs20
Charles
Hi Charles,
I’m testing a bunch of my data for my dissertation so I can do further analysis.
On my last data set my W value came out being super low at 0.6927 (n=12).
As the W values in the chart don’t go down that low does this just mean that I accept the null hypothesis and my data isn’t normally distributed?
Hi Kai,
Since W is lower than the lowest value on the table this means that p-value < .01, which means that you reject the null hypothesis that your data is normally distributed. Charles
Hi there,
I am doing a Shapiro Wilk for n=15 data – however my w value comes out above 1. therefore i cannot continue with the calculations as shown.
Hello Marc,
If you email me an Excel file with your data and calculations, I will try to figure out what went wrong.
Charles
Hey Charles,
Can I send you an email with 2 questions about this in trying to do the same but with few other different things
Yes
Hello Charles,
I also have problem with my n=24 data where the w value exceeds 1 (1.159902956) but I cannot figure out which one is wrong.
Angie
Hello Angie,
If you email me an EXcel file with your data I will take a look at it.
Charles
Thank you very much for your help!
I came accross this paper with tables for W. Just wanted to share 🙂
Rudolph S. Parrish (1992) New tables of coefficients and percentage points for the w test for normality, Journal of Statistical Computation and Simulation, 41:3-4, 169-185,
DOI: 10.1080/00949659208811399
https://sci-hub.tw/10.1080/00949659208811399
Thank you again!
Hello Mercedes,
Thank you very much for sharing this. So far, I haven’t been able to connect to the site, but I will try again tomorrow.
Charles
It is a link to the paper trough Sci-hub, but maybe you cannot connect from your country. Sometimes the links do not work everywhere.
Sorry through 🙂
Hi Charles,
Thank you for your sharing. I have some questions about the normality test in excel.
I do the normality test in excel and spss. But the w value and p value are different.
In excel: w value= 0.953, p value=0.367, while in spss: statistic value=0.952, p value=0.273.
I don’t understand why they are different?
Hope your reply!
thanks
See the response to your previous comment.
Charles
Hello Charles,
Thanks for your sharing. It’s really help me a lot.
While I have a problem.
I do the shapiro-wilk test in excel and spss. But the w values are not equal.
my example: n=25, w value calculated by excel is 0.953, while w value calculated by spss is 0.952, and also the p value is not equal, I used Linear Interpolation to calculate, and the p value calculated by linear interpolation is 0.367, but the p value in spss is 0.273.
I don’t know why they are not equal.
That the W value is different by .001 is not so surprising since some sort of approximation is used. The difference in p-values is likely due to the choice of interpolation techniques. The Real Statistics software (for SWPROB and SWTEST) doesn’t use linear interpolation and in fact returns a value of .293. This too is an estimate. I don’t know whether the SPSS or Real Statistics estimate is better, but both give values that support the assumption of normality.
Charles
Hello Charles,
I have three queries:
1. I am working on three variables EI, CSS and PT(1 independent , 2 dependent
). do i need to to check the normality in totality or of individual construct.
2. After calculating normality using SW test (N=551) EI sig=.054, CSS sig=.056 and PT=.251. plz suggest should i go with it or drop.
3. When i am calculating the same in totality EI+CSS+PT sig=.213
also checked for skweness and kurtosis values they are falling the acceptable limits.
if possible kindly give some references too.
Plz throw some light and give ur suggestions
Hello Daman,
1. It depends on what hypothesis you are testing and what test you are using.
2. The first two are marginal, but probably close enough. The third is clearly out of range for normality. Some tests are pretty robust to violations of normality and so it depends on the shape of the distribution as to whether you can still use that test.
3. Probably not normal, but it is unlikely that your test will require this measurement.
4. Depends on whether you are saying “falling into the acceptable limits” or “failing”. If skewness and kurtosis are falling within the acceptable limits, then it is likely that your data is sufficiently normally distributed. See
d’Agostino-Pearson Test
5. References: See the tutorial at Testing for Normality
Charles
Dear Charles,
Thanks for your great work!
I am new to the data analysis function in excel. I encountered one problem when performing analysis. I have a set of data with sample size of 239 and the p-value of Shapiro-Wilk test displaced is non-numerical (e.g. 6.08116E-08). However, the p-value of Pearson test displaced normally. I am using excel professional plus 2010 version. Could you help me to find out the cause of the problem? Thanks!
Hello Candy,
6.08116E-08 is equivalent to .0000000608116, which is a very small number.
Charles
pls help me. i dont understand how p value calculated? in my case w=0.957575962, that value between 0.9 and 0.95 (n=13). p value is how much? pls tell me method that is how calculate p value thanks
Hello Soko,
Based on the table at https://real-statistics.com/statistics-tables/shapiro-wilk-table/ if W = .974 then the p-value = .90, while if W = .979 then the p-value = .95. Since W = .957575962 is between W = .945 and W = .974, the p-value for your test is between .50 and .90, probably a lot closer to .50 than .90 since .957575962 is closer to .945 than to .974.
Assuming that you have set your significance level at alpha = .05, no matter which value between p-value .50 and .90 you choose, you don’t have a significant result (since any such value is much higher than .05) and so you are safe to assume that your data is normally distributed.
To get a more exact result for the p-value you can use interpolation. The various approaches are described on the following webpage:
https://real-statistics.com/statistics-tables/interpolation/
I believe that the SWTEST function in the Real Statistic Resource Pack uses log interpolation, but the results using linear regression (the simplest type) will give good enough results.
Charles
Hi, I may have missed this small detail, but maybe you would be kind enough to give me some help… I’m using R to calculate the SW test on my data which is 21 and 25 samples. However, I’m having a hard time figuring out how to actually report the results in my paper… is there a good protocol/precedent/format that makes it sound nice and succinct? (I think this is what Sundar was asking also.)
Do I just say something like: After running a SW test for normality W=0.96, p = 0.41, there is no indication that the data set is not normally distributed. (Do I need to included degrees of freedom, or some other #s in there?)
Thanks.
From R:
> shapiro.test(eAp)
Shapiro-Wilk normality test
data: eAp
W = 0.95957, p-value = 0.4059
Matt,
I don’t know whether there is an approved approach. I would simply say that based on the Shapiro-Wilk test, the normality assumption is met. If you want you can insert (p = 0.41).
Charles
Come on Charles answer me.
So, which table is better with small samples, the original or the extended?
Probably the original table, but the results should be similar.
Charles
I agree; however, in your example here-with 12 samples-they aren’t very close. If you’re going to uses exponential estimates to expand Shapiro’s table, I think you need at least 6 exponentials to do a proper job. The worst is small samples.
When using exponential estimates, Excels limit appears to be about 6 exponentials before the 18 digit precision fails.
prof bill -btw, I really appreciate your Excel examples and list your links to my computer wise students. There’s nothing like your examples any where on the internet. thx Dr. Dude!
I am pleased that you and your students are getting value from the Real Statistics website and examples.
Yes, for small samples, the original version should be better.
Charles
Worked like a charm! Thanks for the explanation and resources!
Hi,
I don’t know how to calculate b. There is a specific formula in excel?
Thanx!
Martina,
=SUM(I5:I10)
Charles
Hi Dear from brazil ,
My name is Fernando , thaks for explanation about normality test shapiro wilk , I use it for methods validation in phamaceutical industry ,
I´d like to know how you found the p- value in excel for shapiro wilk ?
best regarding Thank you for your help in this matter
Fernando,
Thank you for your kind remarks.
The p-value comes from the table shown on the following webpage:
https://real-statistics.com/statistics-tables/shapiro-wilk-table/
This based on the work done by Shapiro-Wilk.
Charles
Hi,
I am attempting to use the SWTEST and/or SWPROB functions described above after installing your RealStatistics add-in. Unfortunately, I am receiving errors (The SHAPIRO function works fine, though). I have screenshots of the errors, however, I am unable to paste them into this message. Please advise.
Daniel,
If you send me an Excel file with your data and test results (at least until you get the error message), I will try to figure out what is going on.
Charles
Sir,
I have result Shapiri-wilk test analysis statistics and P-value . My result is 0.-19 and P-value is 0.18. Then what solution is this result. Please kindly reply to How is write interpretation.
Sir,
I have result Shapiri-wilk test analysis statistics and P-value . My result is 0.-19 and P-value is 0.18. Then what solution is this result. Please kindly reply
Sundar,
As explained in Example 1, since p = .19 > .05 = alpha, the result indicates that the normality assumption is satisfied.
In your comment you say that you got a result of 0.-19. I don’t understand what this means.
Charles
How is write interpretation. Thant only sir
Dear sir, run test value -1.39 and p- value 0.16 . Each value -4.95, -5.72. Sir i want this details. Run test value minus value correct or incorrect. Please tell me sir
Sundar,
Sorry, but I don’t understand your messages. If you send me an Excel file with your data and analysis, I will try to help you further.
Charles
Hi,
Can you help me interpret this Shapiro-Wilk Statistic df Sig.
,918** 51 ,002
by age?
Sorry, but I don’t know what ,918** 51 ,002 is referring to. How to interpret the results from the Shapiro Wilk test carried out by Real Statistics is explained on the webpage.
Charles
Hi: Can I fixe a p-value=0.001 for to proof normality?
Giovanni,
You can use alpha = .001, but generally alpha = .05 is used.
Charles
Could you tell the references you used?
Patricia,
The reference is to the Shapiro-Wilk paper. See the Bibliography webpage.
Charles
Hi Charles,
If one gets a value for W = b2/SS = 0.837 < 0.884 (with n=24) which is not in p-value tables, how would you handle that situation? Would this imply that there has been a calculation error or is automatically a reject? Many thanks for putting together this helpful web site!
Julian,
Since the smallest value for n = 24 is .884 (at alpha = .01), this means that p-value < .01, which is usually interpreted as significantly different from normality. Charles
Hi, could you explain me why you use that b formula instead of the “standard” formula used on wikipedia for calculate W? Is there any difference? Thanks
Giacomo,
It should be equivalent to formula shown in Wikipedia. I can’t recall whether I used the version in the original Shapiro-Wilk paper or elected to use the approach that I did to emphasize the symmetry aspect of the calculation.
Charles
Dear Charles,
first I would like to say that the Add-in seems great however I did fail to follow your example by calculating it with the RealStat Add-in for Excel 2016.
I´m using the the “example 1” data set “age”.
Using the add-in I got:
W 0.971066437
p-value 0.921648864
alpha 0.05
normal yes
These results are different from your manual calculations which I could follow and got the same results.
Do you have any idea what the reason is?
I would love to use the add-in but I need to be sure it is working the right way.
Best regards,
Stefan
Stefan,
There are two versions of the Shapiro-Wilk test: the original version, which is described on the referenced webpage, and Royston’s version, which is described on the webpage https://real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/shapiro-wilk-expanded-test/
The add-in value that you describe uses the Royston’ version. Actually, if you look at the output for W from the add-in, it will contain the formula =SHAPIRO(A4,A15). If you change the formula to =SHAPIRO(A4:A15,FALSE) you will get the value of W as calculated by Shapiro-Wilk’s original algorithm (the same is true for the p-value, which is calculated by SWTEST).
The original version works well for smaller samples, but doesn’t support larger samples. This is the advantage of the Royston version.
Charles
My W value is 1.273573913 for 22 samples. I can’t find a table that goes that high, and an online calculator gave me an error. What does this mean?
Jared,
It could mean that you made an error in calculating W. What is the data in your sample?
Charles
Hi, Charles,
thank-you for your very helpful side.
My sample consists of 5 cases (i.e 37;105;110;150;216), resulting W = 0,9762. I want to do the SW-Test with a probability of error of 5%.
Do I have to compare my calculated W with W(p=0,95)=0,986 or with W(p=0,05)=0,762?
Thank you very much for your answer!
Ulrike
Ulrike,
As described on the referenced webpage, if W =.971, then p = .874 (via interpolation between .5 and .9). Since .874 > .05, then we conclude that we don’t have evidence to reject the hypothesis that the data is normally distributed.
Another way to look at this is that if W =.971 >= .762 (the W value at .05), then the data is considered to be normally distributed.
Charles
Thank you very much for your answer!
Meanwhile I downloaded also your AddIn for Excel; that will help me a lot for my work! What a great offer!
Best regards,
Ulrike
Hi admin
This is an excellent explanation for the Shairo-Wilk’s test. This saved lots of time. However, I still have a questions in this test; how are the weight values calculated? What do the mean?
Thank you
Moutaz,
You need to read the original Shapiro-Wilk paper. See Bibliography.
Charles
Thank you very much for the excellent explanation!
For n=4, my calculated value of W is 0.677. The smallest critical value for 0.01 when n=4 is 0.687. How do I interpret this result given that my W value isn’t even within any range given? I’ve double checked my data and don’t see any typos in my data recording or calculations.
Marissa,
This means that the p/value is less than .01
Charles
Thank you. It is really helpful
I tried this on a sample of 41. I got a W = 0,90728. According to the table, the closest value is 0,92 (p = 0,01) – none are lower with the same sample size. Do I just use this value or should some measure be taken?
Also, I need to make sure that I understand the method correctly. The p-value i get from interpolating is the actual p-value and has to be lower than a threshold value (say p = 0,05) in order to reject the null hypothesis – correct?
Thanks in advance
Magnus,
Yes, the approach you are using is correct. Since .90728 < .92, you can deduce that p < .01. In fact, if you sue the Real Statistics formula =PROB(41,.90728) you get the p-value = .002739. Since this is much lower than .05, you do indeed reject the null hypothesis that the data is normally distributed. Charles
Thank you very much.
I have another issue though. What is more reliable (and under what conditions), QQ plot or SW-test? I seem to get a rejection of the null hypothesis using SW, but the QQ show very small devations – or so it appears to me. Is the SW test very sensitive to large (e.g. n = 40) samples?
Magnus,
I find it easier to use the SW test since it is easier to interpret its results, but both are fairly accurate. Also, since most tests are fairly robust to violations of normality, either test can show whether the data is really departing from normality. Both tests can be sued with large samples.
Charles
My entire population is just 30 values. Can the Shapiro-Wilk test also be applied to a population rather than just a sample?
Am I correct in assuming that it is simply a test for symmmetry? My situation is that I have hundreds of datasets of 30 values and I find that even if the dataset is symmetrical the distribution of the values can be a long way from the 68-95-99.7 probability bell-curve.
For example, for one dataset, the number of entries in 1Sd bins from -2sd to 2sd is … 7,4,13,5, which produces a SW p-value of 0.43. In contrast to this distribution the “68-95-99.7” probability curve suggests that a population of 30 should be either 5, 10, 10, 4 or 4, 10, 10, 5.
Is it good practice to identify those datasets where the distribution is a long way from 68-95-99.7? If so, how is that done?
Thanks in advance.
John,
You can use the Shapiro-Wilk test for a population. Shapiro-Wik tests for normality not just symmetry.
Charles
Thanks Charles.
Another question that might interest other readers. I’m using your Excel method and I’ve written a Fortran subroutine to calculate the p_value. With the same input data they give the same results (as they should).
When I put the same data into http://contchart.com/goodness-of-fit.aspx I get a different p-value for the Shapiro-Wilks test.
Before I contact that website to ask them to check their processing, do you have any thoughts on the matter?
John,
I have also checked my results with other programs and they match.
Charles
Can I get the idea how to do the below :
Interpolating .971026 between these value (using linear interpolation)
Salman,
Please look at the following webpage:
Interpolation
Charles
Thank you very much for your excellent explanation and excel workbooks!
Dear Dr. Zaionts,
Thank you very much for your great tool.
I recently downloaded the latest Release (3.5.3) for the Mac version of Excel. In this one, the SWTEST function apparently gives a #VALUE! output with range size greater than 3. Is there a way to fix this? If not, where may I find and download a previous Release?
I thank you in advance for your attention.
Stefano
Dear Stefano,
I don’t think I made any changes to this function since the previous release. In any case, if you send me an Excel file with your data and function results I will try to figure out what is causing this. You can send the file to my email address, which you can find at Contact Us.
Charles
These are the W values I have got from a raw data of response times for n=18.
1,012157199 0,996684879 0,824085184 0,960953212 1,006536182
Most of these values of W are out of range from the (n/p)table. Does that mean I have some calculation errors? If not, then how do I interpret the data?
Pri,
Since W = 0,824085184 is less than the smallest value in the table for n = 18 and p = .01, it just means that p < .01 Actually, I calculate that the p-value = 0,003394 using the Royston approximation that is described elsewhere on the website. This means that your data is likely not normally distributed. Similarly, W = 0,9609532124 is greater than the largest value in the table for n = 18 and p = .99. This just means that the p-value is larger than .99. This means that your data is probably normally distributed. The value W = 0,9609532124 is not in the table, but you know that it occurs between the values p = .5 and p = .9. You can interpolate (as described on the referenced webpage) to come up with an approximate p-value of .59, but in any case the value is much higher than .05, and so the random sample probably comes from a population that is normally distributed. Now the cases where W > 1 are causes for concern since I believe the value for W can’t exceed 1. There is a good chance that you have made a calculation error.
Charles
Hello Dr. Zaiontz,
I really appreciate your examples and web page on real statistics using excel. I tried Shapiro-Wilk test on my data (n=10),however, I have got many variables, so I am testing the normality for each of the variables. So for one of the data, I got W=0.5679 and I referred the Wilk Test sheet, I could not get the P-values. Could something be wrong with my data itself? Or is there an extended table? Please help.
Thanks
Soira,
Since the value for W is less than the critical value at p = .01, you can conclude from the table that p-value is less than .01
Alternatively, you can use the Royston version of Shapiro-Wilk test. See the webpage
https://real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/shapiro-wilk-expanded-test/
In this case, you can calculate the p-value as SWPROB(10,.5679) = 2.3E-05.
Charles
thank you Charles
Hi Charles,
Thanks for the information on the website. It is really useful. However when I applied the Shapiro test to my data it gave me an error. This error does not happen for larger samples (mine is 4) like 5 or 6. Is there a limitation to the excel function that does not allow small samples to be tested with this function?
Thanks
It looks like it should work for samples of size at least 5.
Charles
Hi Charles,
I tried again the Shapiro test on my data and surprisingly it work for a sample size 3 but still not 4… Just thought I should let you know.
Thanks for the website
Joana
Joana,
Thanks for finding this bug.
The original test for sample size of 4 does work (setting the second argument in the SHAPIRO or SWTEST function to False). The Royston version of the test has the bug when the sample size is 4.
I will provide a fix in the next release.
Thanks again for helping me improve the accuracy of the software.
Charles
I have gone through your explanation and I found very rewarding and useful. However, will appreciate an example for sample that is odd and not even like your two examples.
Regards
Tony,
The sample in the second example has an odd number of elements. The middle element is not used.
Charles
I want to know what happens if data fails the SW test?
Is there any way out?
Jerry,
If data is not normally distributed, then for tests that assume normality you can
1. use a nonparametric test that doesn’t require normality
2. transform the data so that the resulting data is sufficiently normal
In addition, some tests that require normality (e.g. the t test) are sufficiently robust that as long as the data is symmetric the test will usually be ok (although even in these cases, the Mann-Whitney nonparametric test should give similar results).
Charles
Thank you Dr. I am learning a lot from your useful website. When I tried Real Stat for Shapir0-Wilk test for the two data given in the two examples, I get different W and p values from those given in the examples, as follows:
W=b^2/SS 0.971025924 W 0.971122526
0.5 0.943 p-value 0.922200674
0.9 0.973 alpha 0.05
p-value 0.873679 normal yes
W=b^2/SS 0.873965213 W 0.874012
0.02 0.855 p-value 0.03866
0.05 0.881 alpha 0.05
p value 0.041882692 normal no
Could you please explain why the difference? Have I committed any mistake in the calculations?
I don’t know why you get different results. If you send me a spreadsheet with your calculations I will try to understand why there is a difference.
Charles
how is analysis durbin watson test using excel or spss software. Please tell step by step sending my email id
The example 1 is well explained. However, my linearly interpolated value of Wc (p-value) comes out to be 0.89999 instead of 0.876681. The interpolation coeffcient is 0.075 per probability of .1, between 0.5 and 0.9. Hence for approx. diff. of 0.002 in W (0,973-0,971), p value = 0.89999. Pl. correct me if wrong.
The calculation I used was to interpolate between the table values .973 – .943 = .03 and .9 – .5 = .4. So the answer is .9 – .002/.03 * .4 = .873.
In any case, the value is far more than .05. Note that you can get a more exact value (which doesn’t require interposlation) by using the Royston approximation, as described on the webpage https://real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/shapiro-wilk-expanded-test/
Charles
Hi Charles,
I found this webpage is very useful and it guided me so well. Thank you very much. But I would like to know something..How will you rank this test with respect to A-D and K-S test?
Shreya
Hi Shreya,
I would use SW over KS. I have not used AD and so don’t have an opinion.
Charles
Hi Charles,
Thanks a lot for this web page!!
You said that the function SWTEST ignore all empty and non-numeric cells. Sure? Because if I add empty cells at the end of the range R1, the p-value is different.
Also, what is the difference between the original Shapiro-Wilk test and the Royston algorithm, and when do you one or the other? (Meaning that I don’t know if in the SWTEST I have to write “FALSE” or “TRUE”.
Thank you very much!
Julien
Hi Julien,
I just retested the SWTEST and SHAPIRO functions by adding empty and non-numeric cells at the beginning, end and in the middle of the range. The results are all the same. Which version of Excel are you using?
If the values you are looking for are found in the table then you might as well use the original algorithm (although the results using the Royston algorithm are quite similar). Otherwise you should use the Royston algorithm. I tend to use the Royston algorithm always since in that case I don’t need to make any decisions.
Charles
I use Microsoft Excel for Mac 2011 in English
Julien,
Which version of the Real Statistics Resource Pack do you have? You can find this out by entering =VER() in any cell. If it is not one of the latest releases (Release 2.15) then this could account for the problem.
Charles
Hi Charles,
It’s the release 2.10.1
Julien,
This is the latest version of the software for the Mac, but it doesn’t contain some of the features that I have added for Windows. In particular WTEST only returns the one-tailed version of the test. You just need to double the value to get the p-value for the two-tailed test. I hope to get a new version for the Mac out soon (as soon as I can get a Mac computer to test it on).
Charles
Julien,
Now I understand the problem. I have not yet updated the Mac version of the software with the latest features. This is why some of the arguments don’t work and why some of the functions don’t handle missing data the same way. My problem is that I don’t have a Mac myself and need to borrow one to test and update the software.
Charles