Regression Analysis – Advanced

Property 1:

image1711

image1712

image1713

Proof: The first and last equations are trivial. We now show the second. By the first equation:

image1714

Taking the sum of both sides of the equation over all values of i and then squaring both sides, the desired result follows provided

image1715

This follows by substituting ŷi by bxi + ai and simplifying.

Property 2:

image1720

Proof: We give the proof for the case where both x and y have mean 0 and standard deviation 1. The general case follows via some tedious algebra.

In the case where x and y have mean 0 and standard deviation 1, by Theorem 1 of Method of Least Squares and Property 1 of Method of Least Squares, we know that for all i

image3471

Since
image3450

it follows that

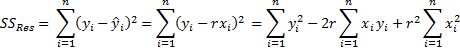
image3473

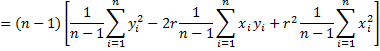
image3474

image3475

But
image3476

and so n – 1 = SST, which means that

image3478

Property 3:

image1721

Proof: From Property 2, solving for r2, we have the following by Property 1:

image5044

Property 4:

image1724

image1725

Proof: The first assertion is trivial. The second is a consequence of Properties 1and 2 since

image1726

Property 5:

a)  The sums of the y values is equal to the sum of the ŷ values; i.e. \sum_i{y_i} = \sum_i{\hat{y_i}}

b)  The mean of the y values and ŷ values are equal; i.e. ȳ = the mean of the ŷi

c)  The sums of the error terms is 0; i.e. \sum_i{e_i} = 0

d)  The correlation coefficient of x with ŷ is sign(b); i.e. rxŷ = sign(rxy)

e)  The correlation coefficient of y with ŷ is the absolute value of the correlation coefficient of x with y; i.e. r_{y\hat{y}} = |r_{xy}|

f)  The coefficient of determination of y with ŷ is the same as the correlation coefficient of x with y; i.e. r_{y\hat{y}}^2 = r_{xy}^2

Proof:

a) By Theorem 1 of Method of Least Squares

image3479

and so
image3480

b) That the mean of the ŷi is ȳ follows from (a) since the mean of ŷ = \sum{} ŷi/n = \sum{} yi/n = ȳ.

c) This property follows from (a) since

image3482

d) First note that by Property 3 of Expectation

image3483

and so
image3484

Now by Property A of Correlation

image3485

image3486

Thus, r = 1 if b > 0 and r = -1 if b < 0. If b = 0, r is undefined since there is division by 0. By Property 1 of Method of Least Squares, r = sign(b) = sign(rxy).

e) Using property (b), the correlation of y with ŷ is

image3488

By Theorem 1 of Method of Least Squares

image3479

for all i, and so
image3489

As we saw in the proof of (d),

image3484

and so putting all the pieces together, we get

image3490 image3491

By Property 1 of Method of Least Squares, r = sign(b) = sign(rxy), and so

image3493

f) This follows from (e),

2 thoughts on “Regression Analysis – Advanced”

  1. Hi Charles,
    I am working with isotope data in tree rings. I simply want to explore whether a linear decline in the isotope time series is significant. I have used a complex, non-intuitive boot strapping procedure in the past but I would prefer to use something more along the lines of simple linear regression model but whenever we do receive somewhat valid critiquies of repeated measures and potential autocorrelation issues. Is there a simple method that I can use to check the concerns or a simple model I can employ?

    Reply

Leave a Comment