Expected Value
Definition 1: If a discrete random variable x has frequency function f(x) then the expected value of the function g(x) is defined as
The equivalent for a continuous random variable x is
where f(x) is the probability density function. This is the total area between the curve of the function h(x) and the x-axis where h(x) = f(x)g(x). For those of you familiar with calculus
In order to avoid using calculus, we will restrict ourselves to the discrete case in the rest of this chapter, although all the results shown here for discrete random variables extend to continuous random variables. Click here for more details about how to extend the results presented here to continuous distributions.
Property 1: For any random variables x and y and constant c
- E[c] = c
- E[cg(x)] = cE[g(x)]
- E[g(x) + h(x)] = E[g(x)] + E[h(x)]
- E[xy] = E[x] ∙ E[y] if x and y are independent
Proof: (a) – (c) are simple consequences of Definition 1. (d) is a consequence of Property 2 of Discrete Distributions.
Population Mean and Variance
Definition 2: If a random variable x has probability density function f(x) then the (population) mean μ of f(x) is defined as
Here the function g(x) in Definition 1 is the identity function g(x) = x.
The (population) variance σ2 is defined as
Property 2: The variance can also be expressed as
Proof: By Property 1,
![]()
Property 3: For any random variable x and constants a and b
Proof: The first assertion is a consequence of Property 1c, namely
For the second assertion, by Properties 1 and 2, we have
![]()
![]()
It follows from Property 3 that for any constant b, Mean(b) = b and Var(b) = 0.
Property 4: For random variables x and y
If in addition, x and y are independent, then
Proof: The first assertion follows from Property 1:
For the second assertion, by Properties 1 and 2
![]()
![]()
But by Property 1d, E[xy] – E[x]E[y] = 0 since x and y are independent, and so
![]()
Standardization
Definition 3: For any random variable x with mean μ and standard deviation σ, the standardization z of x is defined by
Property 5: The standardization of any random variable has a mean of 0 and a variance of 1.
by Property 3 the mean of z is
Excel Function: Excel provides the following function for calculating the value of z from x, μ, and σ:
STANDARDIZE(x, μ, σ) = (x – μ) / σ
Real Statistics Function: The Real Statistics Resource Pack provides the following array function for the array or cell range R1.
XSTANDARDIZE(R1) = STANDARDIZE(R1,AVERAGE(R1),STDEV.S(R1))
Moments
Definition 4: The nth moment around the mean is defined as
Click here for more advanced information about moments and related subjects.
Observation: It follows from Definitions 2 and 4 that the variance can be expressed as
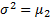 Skewness and Kurtosis
Skewness and Kurtosis
In Symmetry and Kurtosis we define the skew and kurtosis of a sample. We now define the population equivalents of these concepts as follows.
Definition 5: The (population) skewness is defined as
The (population) kurtosis is defined as
The 3 in the kurtosis definition is the value of μ4/σ4 for the normal distribution function (see Normal Distribution). Thus the kurtosis of the normal distribution function is 0.
Reference
Wikipedia (2012) Expected value
https://en.wikipedia.org/wiki/Expected_value
Penn State (2021) Mathematical expectation. Introduction to probability theory
https://online.stat.psu.edu/stat414/lesson/8
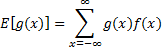
For property 4, it implicitly state that x and y are independent through the proof process.Iit will be clearer if we can have the conditional statement (if only x and y are independent) for the variance addition.
Sun Kim,
Thanks for catching this error. As you have stated, the second assertion depends on x and y being independent, as is clear from the proof.
I have now corrected the webpage. I appreciate your help in making the Real Statistics website clearer and more accurate.
Charles
I was looking for the information on moments, the link given above is not working. Could please provide with the working link. Your explanation and derivation is very intuitive.
Thanks Regards
Harsha
Harsha,
Sorry about that. I have just repaired the link. In any case, here is the link that I believe that you are looking for
https://real-statistics.com/general-properties-of-distributions/advanced-properties-of-distributions/properties-probability-distributions-detailed/
Charles
Hi,
a little error here
Sigma/Sigma^2 = 1
To correct, Signa^2/Sigma^2 = 1
This web site is awesome. It’s really useful providing many excel add-in functions.
Thanks, Sir
Hi Mobb,
I am very pleased that you like the website.
I also appreciate your identifying the typo. I have now corrected the error on the referenced webpage. Thanks for catching it.
Charles