Property 1: Given samples {x1, …, xn} and {y1, …, yn} and let ŷ = αeβx, then the value of α and β that minimize 
Proof: The minimum is obtained when the first partial derivatives are 0. Let
Thus we seek values for α and β such that 
Property 2: Under the same assumptions as Property 1, given initial guesses α0 and β0 forα and β, let F = [f g]T where f and g are as in Property 1 and
Now define the 2 × 1 column vectors Bn and the 2 × 2 matrices Jn recursively as follows
Then provided α0 and β0 are sufficiently close to the coefficient values that minimize the sum of the deviations squared, then Bn converges to such coefficient values.
Proof: Now
Thus
The proof now follows by Property 2 of Newton’s Method.
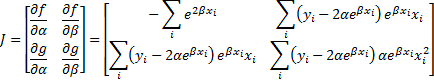
Hi Charles:
Regarding Question 1, it is standing no more. I thought it was the Fcrit, but instead it is like the p-value, then it does have the value you presented. Sorry for my confusion.
Question 2 still stands.
All the best.
Hi Charles:
I find your site very interesting and useful. Thanks for the great effort !!!
In your “Exponential Regression using Newton’s Method” page, it does not have a “Leave a Reply” at the end, so I am posting here. Sorry for any inconvenience.
Question 1. In Figure 3. Which is the formula for “Significance F”…is it “=F.INV(0.05, 1, 9)”? If that is the case, Excel gives the result of 0.00416, but you have 1.175E-06.
Question 2. Which is the rationale to have the formulas in cells Q25 and Q26, for the standard error of a and b (alfa and beta)? I mean, why you take values from the JTJ-1 matrix? Please clarify the reason.
Thanks in advance for the clarifications.
Jorge,
Question 2: This is how Newton’s Method works. See the following webpage:
https://real-statistics.com/matrices-and-iterative-procedures/newtons-method/
Charles