Confidence and prediction intervals for forecasted values

Objective

On this webpage, we explore the concepts of a confidence interval and prediction interval associated with simple linear regression, i.e. a linear regression with one independent variable x (and dependent variable y), based on sample data of the form (x1, y1), …, (xn, yn). We also show how to calculate these intervals in Excel. In Confidence and Prediction Intervals we extend these concepts to multiple linear regression, where there may be more than one independent variable.

Confidence Interval

The 95% confidence interval for the forecasted values ŷ of x is

Confidence interval regression

where
image1773

Here, sy⋅x is the standard estimate of the error, as defined in Definition 3 of Regression Analysis, Sx is the squared deviation of the x-values in the sample (see Measures of Variability), and tcrit is the critical value of the t distribution for the specified significance level α divided by 2. How to calculate these values is described in Example 1, below.

The 95% confidence interval is commonly interpreted as there is a 95% probability that the true linear regression line of the population will lie within the confidence interval of the regression line calculated from the sample data. This is not quite accurate, as explained in Confidence Interval, but it will do for now. 

 Confidence prediction interval

Figure 1 – Confidence interval

In the graph on the left of Figure 1, a linear regression line is calculated to fit the sample data points. The confidence interval consists of the space between the two curves (dotted lines). Thus there is a 95% probability that the true best-fit line for the population lies within the confidence interval (e.g. any of the lines in the figure on the right above).

Prediction Interval

There is also a concept called a prediction interval. Here we look at any specific value of x, x0, and find an interval around the predicted value ŷ0 for x0 such that there is a 95% probability that the real value of y (in the population) corresponding to x0 is within this interval (see the graph on the right side of Figure 1). Again, this is not quite accurate, but it will do for now.

The 95% prediction interval of the forecasted value ŷ0 for x0 is

Prediction interval regression

where the standard error of the prediction is

Standard error prediction

For any specific value x0 the prediction interval is more meaningful than the confidence interval.

Example

Example 1: Find the 95% confidence and prediction intervals for the forecasted life expectancy for men who smoke 20 cigarettes in Example 1 of Method of Least Squares.

Confidence prediction intervals Excel

Figure 2 – Confidence and prediction intervals

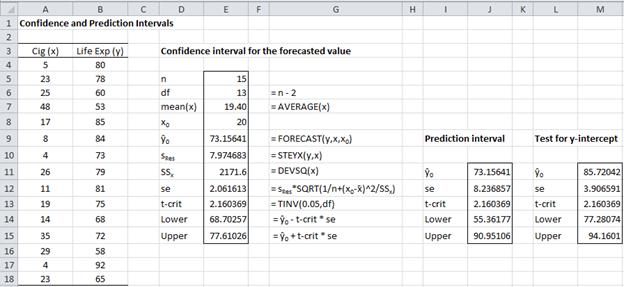
Referring to Figure 2, we see that the forecasted value for 20 cigarettes is given by FORECAST(20,B4:B18,A4:A18) = 73.16. The confidence interval, calculated using the standard error of 2.06 (found in cell E12), is (68.70, 77.61).

The prediction interval is calculated in a similar way using the prediction standard error of 8.24 (found in cell J12). Thus life expectancy of men who smoke 20 cigarettes is in the interval (55.36, 90.95) with 95% probability.

Graphical representation

You can create charts of the confidence interval or prediction interval for a regression model. This is demonstrated at Charts of Regression Intervals. You can also use the Real Statistics Confidence and Prediction Interval Plots data analysis tool to do this, as described on that webpage.

Testing the y-intercept

Example 2: Test whether the y-intercept is 0.

We use the same approach as that used in Example 1 to find the confidence interval of ŷ when x = 0 (this is the y-intercept). The result is given in column M of Figure 2. Here the standard error is

image1782

and so the confidence interval is

image1783

Since 0 is not in this interval, the null hypothesis that the y-intercept is zero is rejected.

Reference

Howell, D. C. (2009) Statistical methods for psychology, 7th ed. Cengage.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf

185 thoughts on “Confidence and prediction intervals for forecasted values”

  1. Hello!
    I’m using a simple linear regression to predict the content of certain amino acids (aa) in a solution that I could not determine experimentally from the aas I could determine. I want to place all the results in a table, both the predicted and experimentally determined, with their corresponding uncertainties. By replicating the experiments, the standard deviations of the experimental results were determined, but I’m not sure how to calculate the uncertainty of the predicted values. I could calculate the 95% prediction interval, but I feel like it would be strange since the interval of the experimentally determined values is calculated differently. In the end I want to sum up the concentrations of the aas to determine the total amount, and I also want to know the uncertainty of this value. How do you recommend that I calculate the uncertainty of the predicted values in this case?

    Reply

  2. Hi Charles, thanks for getting back to me again. I’m trying to establish the confidence level in an upper bound prediction (at p=97.5%, single sided) . I used Monte Carlo analysis with 5000 runs to draw sample sizes of 15 from N(0,1). In order to be 90% confident that a bound drawn to any single sample of 15 exceeds the 97.5% upper bound of the underlying Normal population (at x =1.96), I find I need to apply a statistic of 2.72 to the prediction error. As I’m doing this generically, the 97.5/90 interval/confidence level would be the mean +2.72 times std dev, i.e. x =2.72. As far as I can see, an upper bound prediction at the 97.5% level (single sided) for the t-distribution would require a statistic of 2.15 (for 14 degrees of freedom) to be applied. A prediction upper bound (such as at 97.5%) made using the t-distribution does not seem to have a confidence level associated with it. So my concern is that a prediction based on the t-distribution may not be as conservative as one may think….

    Reply

    • Ian,
      Since the sample size is 15, the t-statistic is more suitable than the z-statistic.
      I don’t understand why you think that the t-distribution does not seem to have a confidence interval.
      Charles

      Reply

  3. Hello Charles,
    Your material has been very helpful in enhancing my understanding of statistics, for which I’m very grateful.

    Does the following interpretation of CI & PI with the context of sampling distribution seem appropriate to you?

    Sampling Distribution of the Mean of Y
    If all possible samples, m, of sample size n were taken for a specific value of X (i.e. X = h), and mean (μy) calculated for the Ys observed against those Xs, then :
    1) The distribution of such means will be normally distributed.
    2) 95% of the confidence intervals (μy ± 1.96σ) calculated from such estimated means will contain the true population mean of Y.
    3) Mean of all the m means will be equal to the overall population mean of Y.

    But since its not practical to take all possible samples of size n, we take 1 sample of size n, and calculate mean of y.

    Confidence Interval for Y
    We expect that, μy obtained from this one sample is one of those 95% that will yield a confidence interval that will contain the true population mean of Y.

    Prediction Interval for Y
    The 95% prediction interval (that has a much wider reach than the confidence interval) calculated using the μy obtained from this one sample will contain 95% of all the possible population values of Y.

    Have I got the interpretation for CI & PI right ?

    Reply

    • Rahul,
      1. A 95% confidence interval for any parameter would mean that if the same experiment is repeated a large number of times, then 95% of the confidence interval calculated from each experiment would contain the true (population) value of the parameter. The true value of the parameter is not guaranteed to be in the confidence interval of the one sample that is drawn. Thus, the phrase “…this one sample is one of those 95%…” in your definition of the Confidence Interval for Y is not correct.
      2. For the confidence interval of a regression model the parameter is the mean μy.
      3. For the prediction interval of a regression model the parameter is any one of the predicted y values.
      Charles

      Reply

  4. Thank you for the explanation.

    Follow on question, is there a way to calculate the confidence interval bounds if I was to force my trendline to go through the origin? Currently, the trendline as a y-intercept value.

    Reply

  5. Dear Charles,

    Thanks for the nice explanations on this website. If the prediction bands and CI bands of a couple of regression lines with unequal slopes (interacion effect) are known, is it then possible to calculate the SE of difference between two regression lines at the mean x?

    The data I want to analyse usually gives divergent regression lines and I want to do post hoc tests with the interpolated values at the mean x. I can do this analysis with Minitab, but I do not understand how they calculate the SE of difference. Do you know where I can find a method to do this?

    Thank you very much,

    Bart

    Reply

    • Hello Bart,
      Sorry, but I am not familiar with the Minitab analysis, and so I am not able to answer your question. In fact, when you reference SE I am not sure whether you are referring to the standard error of the slope or something else.
      Charles

      Reply

  6. Hi Charles,
    Really appreciate your quality lecture note.
    May I ask the derivation of s.e.(standard error of the prediction) formula?
    Thank you!

    Reply

  7. Dear Charles,
    You discussed here how to predict (Y) value from (X) and how to estimate its confidence interval. In my stydies, I use the regression equation to predict (X) value from (Y) as in the following example:
    Conc (X) Response % (Y)
    10 20
    15 27
    20 35
    25 46
    30 55
    35 70
    40 85
    Regression line equation: Response% = Slope * Conc. + Intercept
    = (2.15) * Conc. + (-5.46)
    Then the concentration that cause 50% response will be:
    Concentration = (50 + 5.46) / 2.15 = 25.79
    My question is how to calculate the Confidence interval of this predicted concentration to get the lower and upper predicted values (X ± ???).
    Please help me and give your answer in steps with an example.
    Sincerely,

    Reply

  8. Hello,

    Thanks for the article. I have a question, which might not be so related to this article, but still about confidence and prediction intervals.

    I’m using lmfit for python. It provides function for confidence interval, but not prediction interval. Its documentation cites the code it is based on, and it has prediction interval calculation.

    https://www.astro.rug.nl/software/kapteyn/kmpfittutorial.html#confidence-and-prediction-intervals

    It uses different formula for standard error. I don’t know if it will hold the same value as the formula here, or their relationship; too complicated for me. Still, I want to have prediction interval, so I want to modify the function in the lmfit module to support it.

    There, the difference between confidence and prediction interval is that err*err is added to the standard error for the prediction intervals. However, in the code, that err is the noise added to smooth model to simulate real data. I don’t think I can get the real noise from real data. I can only get residuals, but the calculation of residuals (and derivation) is also weird there (they’re divided by err), which adds more confusion for me.

    Below the definition of err in the code, there’s a commented out line of err that makes err a straight 1 for the length of the dataset. If err is 1, then err*err is also 1, so it will just add 1 to the standard errors before they are sqrt-ed. I notice that here in your article, the difference of standard error formula for confidence interval and prediction interval is that 1 is added there before it is sqrt-ed. This doesn’t seem like coincidence for me. So, my question is, can I just change err*err with 1?

    Thank you

    Reply

    • Hello Rizqi,
      I am not familiar with the lmfit module, and so I can’t comment on it.
      As you can see from the referenced Real Statistics webpage, the only difference in the calculation between a prediction interval and a confidence interval is an extra 1 under the square root symbol.
      Charles

      Reply

      • Thank you for the response. Sorry, I knew this was kind of unrelated.

        I tried adding 1 there, and the prediction interval is now very wide compared to confidence interval. It encompasses all data points. Also, the width of prediction interval when the confidence interval is or close to 0 is the same or almost the same as the sigma (there I use sigma=3). If I change sigma to 2 it’d be 2.

        https://ibb.co/x273fbD

        Is that just how it is? Or is this just wrong?

        Reply

  9. Hi Charles,

    I ran a regression model and added confidence and prediction interval. While most of the data points stay within the prediction band, there are some outside the prediction band. I’m having trouble interpreting those points, in general, do those points mean that they are outliers?

    Reply

    • Leonardo,
      Yes, in some sense these points are potential outliers for the regression model, but if you have a lot of points you can expect that some will lie outside the prediction band.
      Charles

      Reply

  10. Hi Charles,
    Thank you so much for the post.
    I have a question, can we have prediction interval for independent variable if dependent variable is already given. I mean if i m using regression line to predict x value as y value is given, can we calculate prediction interval for x value also.

    Reply

  14. Is this statement true: ”If we estimate a regression slope, its confidence interval represents a plausible range for the slope’s true population value.”?

    Reply

  15. Hi Charles,
    Is it the same formula to calculate prediction intervals for non-linear functions too (i.e. Weibull, Gompertz)?

    Thanks,

    Reply

    • Hello David,
      The situation will be different. Here is an article about the prediction interval for the Weibull distribution.
      lib.dr.iastate.edu/cgi/viewcontent.cgi?article=1011&context=stat_las_preprints
      Charles

      Reply

  16. Hi Charles,

    In a question where they would a model that related the annual number of Australian wines sold to the annual growth rate of Canada, what would be x and what would be y?

    Albert

    Reply

  17. Thanks for a very useful post!

    Just wondering, how would you go about calculating a random set of best-fit lines with those confidence intervals? I guess I would have to determine a distribution for the set of possible slope and a distribution for the set of possible intercept values?

    David

    Reply

      • No idea… I just referring to the plot on the right of the first figure that shows a selection of regression lines withing the confidence intervals, and wondering how one would go about getting a random sample of those regression lines?

        Something like bootstrapping resampling with a t-test to get the ones that are within the 95% interval?

        Reply

        • David,
          Here’s my rough idea for how you might go about doing this. Let’s look at a specific example, namely Example 1 on
          Plot of Confidence and Prediction Interval
          First look at the mean of the X values, namely x = 19.4. Next calculate the upper and lower bound for the y value corresponding to this value of x. Suppose for a minute that the mean of the x values is 20 (i.e. it is one of the sample data values for x) instead of 19.4. Then, as we can see from Figure 1, the the lower and upper bound for the corresponding y value is 68.70 and 77.61. Now pick a value between 68.70 and 77.61 at random: e.g. by using the formula =68.70+RND()*(77.61-68.70). Say this value is 71.22. Next we pick any other sample x data value, say 0. The corresponding y value ranges from 77.28 and 94.16. Once again pick a value at random from this range. Say this value is 88.42. Now this random line connects the points (20, 71.22) and (0, 88.42). We can use easy express the equation for this line in the form y = mx + b.
          It was important to start with the mean value for x so that the two randomly assigned points would stay within the confidence interval. Thus, the only thing left is figure out the range of y values corresponding to the mean value of the x when this value of x doesn’t correspond to any of the points in the sample. I guess some sort of curve fitting approach could be used.
          Charles

          Reply

  18. Hi Charles,

    I’m just starting to uses your excel add-in and it works great for graphically presenting the confidence and prediction intervals for a simple linear regression. Thank you! I’m trying to calculate and graphically display tolerance intervals with 95% confidence and 75% coverage of the population. I’m not seeing those options in your confidence and prediction interval. Do you offer these options in your add-in?

    Reply

  19. Hello,

    I am evaluating the concentration of a chemical in blood in relation to its concentration in the food. I derrived a linear regression and the respective prediction intervals. Now, I would like to calculate how many samples I have to analyse to predict the right concentration ( with e.g. 95% confidence) in the food. How can I do this?

    Best regards
    Suse

    Reply

    • Susanne,
      You have created a linear regression model based on one sample with a number of elements. This model can be used to make predictions. If you create a new sample you will get a different (hopefully not very different) regression model. Thus, it is not clear what you mean by “how many samples…”
      One way to interpret your question is to assume that there is some commonality between the samples; e.g. you fix the values of the x mean, x standard deviation and the correlation coefficient between the y and x values. As can be seen from the formula for the prediction standard error on this webpage, s.e. depends on the x mean, S_x (related to the x standard deviation) and s_y.x (related to the correlation coefficient and sample size n). The size of the prediction interval is twice s.e times t-crit. Here t-crit depends on df, which is n-2. Thus for fixed values of x mean, x standard deviation and correlation between y and x (and x_0), the size of the prediction interval only depends on the sample size n (using the formulas for s.e. and df). If you fill in the values of these three values in Figure 2 on the webpage (e.g. based on the linear regression you already developed), the only remaining variable is the sample size n. You can then manually repeatedly change the value of n (cell E5) until you get the prediction interval size (i.e. the value of =J15-J14) that you desire. You can also use Excel’s Goal Seek to calculate this for you.
      Charles

      Reply

  20. Dear Charles
    Thank you for your useful text, but I would so appreciate if you would advice me how can I plot these confidence intervals for multiple linear regression with more than one variable, please. and I have more question, may you kindly tell me how can I have the equations of these confidence interval lines, for using in predicting models, please?

    Best Regards

    Mojgan

    Reply
  21. Pingback: Paul Connett’s misrepresentation of maternal F exposure study debunked | Open Parachute

  22. Hello Dr. Zaiontz,
    I have a doubt regarding prediction interval calculation.Does the calculation depend on method of forecasting used?(e.g. ARIMA, linear regression, ETS) Or it’s independent of methods used for forecasting.Please give me some references to look at for support of your answer.
    Thanks in advance.

    Reply

    • Arka,
      This webpage specifically addresses forecasts using linear regression (with one independent variable). The techniques will vary depending on which model you use (ETS, ARIMA, etc.)
      Charles

      Reply

  23. Hello Dr. Zaiontz,
    I am developing a correlation between sample lab results (x) and field instrument readings (y) in order to establish a cleanup level equivalent for my field instrument. I’ve calculated 95% upper and lower prediction limits for the field instrument cleanup value equivalent and would like to know what I can say precisely about each of these values. Is it accurate to say of the lower prediction limit that there’s a 95% (or 90%?) chance that the true field instrument cleanup value equivalent is greater than the lower limit and that this value assures minimal false negatives (null hypothesis is that contamination exceeds cleanup level)? Similarly, is there a 95% (or 90%?) chance that the true field instrument cleanup value equivalent is less than the upper limit? If the latter is accurate, what would be any potential value of using the upper limit, other than it being the least conservative value (i.e. allowing minimize cleanup costs) without regard for false negatives?
    Thanks

    Reply

    • Keith,
      In general if you have a 95% confidence interval for some parameter of (a,b), it means that if you reran the experiment 1,000 times, then the true value of the parameter will occur in the interval (a,b) in approximately 950 (i.e. 95%) of these experiments.
      Charles

      Reply

  24. Charles Zaiontz,

    I need to say that you are such an absolutely amazing person. All your intructions are very easy to follow. I even like statistics now. Thank you very much!

    Reply

  25. Hello Charles-

    I am being asked to use the slope and intercept to create a nonlinear model, after I have identified my most linear graph which is the “Power Regression” model. With my regression summary statistics, how am I creating the formula using slope and the intercept. I am missing something rather simple I believe.

    Thanks,
    Cristopher

    Reply

  26. Hi Charles,
    Thanks for maintaining this site with very helpful information.

    Is it a good idea to use the prediction intervals as a check for outliers in the measured data when doing a linear regression between y and x?

    Best regards
    Tomas

    Reply

  27. Hi Charles,

    I would like to know how to calculate the “Standard Error of intercept” or “Standard deviation of intercept” by excel formula rather than LINEST function?

    Thanks for your informative helps
    Chester

    Reply

    • Mark,

      I believe that the type of linear regression that you are referring to is described on the following webpage:
      Multiple Regression without Intercept. The value for the matrix B is given on that webpage.

      The calculation of the prediction interval is shown on the following webpage:
      Confidence and Prediction Intervals for Multiple Regression. You can use the formula on that webpage for the prediction interval substituting the value B given above.

      Charles

      Reply

      • Sorry if I wasn’t specific enough, but I am using a simple linear regression thought the origin (zero-intercept). What is the equation for the confidence interval for the forecasted values ŷ of x? Wouldn’t it be that s.e.=0 when x=0 such that any and all possible true best fits still goes through the origin and do not rotate around the data set mean (curved confidence interval)? Thanks again.

        Reply

        • Mark,
          Clearly at x = 0, s.e. would be zero, but this is not the case for other values of x.
          The information I gave you previous will enable you to calculate a prediction interval at other values of x.
          Charles

          Reply

  29. Hi Charles,

    I’m fitting a regression model to some lifing data (Strain vs Number of Cycles) and would like to make sure I’m making the right assertions.

    When regression isn’t involved, I’ve seen several references to tolerance intervals. (I think this is what Tristan was referring to when he spoke about 98% of the population with 95% reliability.)
    I’m still struggling slightly with the differences between prediction and tolerance intervals (explained in https://en.wikipedia.org/wiki/Tolerance_interval), particularly in the context of a regression model. I was hoping you might be able to explain and have some pointers about how to modify the calculations to include it.

    Ideally I’d like to say for a certain value of strain (X) for a design we can be A% confident that B% of the population will survive beyond Y cycles.

    Many thanks for your help.

    Reply

    • Roger,
      Sorry, but what do you consider to be the pooled within-group regression slope as obtained from ANOVA?
      Charles

      Reply

    • Roger,
      Sorry, but what do you consider to be the pooled within-group regression slope as obtained from ANCOVA?
      Charles

      Reply

      • Hi Charles
        I am not a statistician – please bear this in mind.

        When you have two variables (x,y) and several groups, one can use an analysis of covariance to test the difference between groups for y when regressed against x. This does not use the regression line with the data pooled irrespective of group, but the pooled within group regression line. For example Statistical Methods, Snedechor and Cochran Chapter 14 fig 14:6:1 (6th ed) . I want the prediction intervals around this pooled-within-group regression line. I hope this is clear.
        Roger

        Reply

        • Sorry Roger, but I don’t have access to Statistical Methods, Snedechor and Cochran Chapter 14 fig 14:6:1 (6th ed).
          Charles

          Reply

  33. Thank you so much! This example was extremely helpful in finding prediction intervals in Excel and exactly what I was looking for!

    Reply

    • Steve,

      Since you are treating ln(y) = ln(a) + bx as a linear regression z = bx + c where z = ln(y) and c = ln(a), one approach to creating a confidence interval is to use the confidence interval for z = bx + c, as described on the webpage
      https://real-statistics.com/regression/confidence-and-prediction-intervals/

      This will give you a confidence interval for z of form [h, k] you then need to convert this into a confidence interval for y. The simplest approach for this is to use the confidence interval [e^h, e^k].

      Charles

      Reply

  35. Everything seems to follow in my software (i wanted to transfer confidence intervals into a bespoke dashboard from my software) for a single X variable
    If i have two x variables how do i calculate the SE of the overall confidence interval?
    I.e what does the Equation in cell G12 look like?

    Reply

  36. Hello charles,

    Thank you for the explanation. I have a question though:
    what if I have x and I would like to predict y instead but with a confidence interval? is it the same principle and the same formula?

    Reply

  37. Hello Charles,

    Could you tell me what the first part in cell G12 is (it is kind of blurry on my monitor), for the calculation of s.e. 2.06?

    Also, is there a shortcut (function) in Excel for the s.e. calculation?

    Thank you,

    Reply

    • John,

      Cell G12 contains the following formula: s_Res * SQRT(1/n + x_0 – k) – 2/SS_x)

      There is no Excel formula for calculating this. The Real Statistics form REGPRED will automatically calculate the s.e. in the prediction interval case, but not the confidence interval case. I will add a similar formula for the confidence interval shortly. See the following webpage for more details:
      Prediction and Confidence Intervals

      Charles

      Reply

  38. Hi Charles,

    If I understand you correctly, you describe the confidence interval as the range of possible values for model parameters, e.g. the range of values slope and intercept may be for a linear regression for a given set of data and specified confidence interval. You describe prediction interval as the interval around a predicted Y for a specific X0.

    However, in your example you calculate confidence interval for a specific X0 and do the same for a prediction interval. I am confused as the example does not appear to match the discussion.

    Obviously I don’t understand you correctly!

    On a related matter, when one does a linear regression with Excel, Excel reports the Lower and Upper confidence intervals for “intercept” and “X Variable”, i.e. values for the slope and intercept. How does this Excel output relate to your discussion above?

    Thank you

    Reply

    • Gary,
      I will respond to your first question shortly.
      Regarding your second question: the confidence intervals for the intercept and x variable are really for the intercept and x coefficient (not for the prediction or confidence interval of data elements).
      Charles

      Reply

    • Gary,

      Here is my response to your first question:

      The confidence interval focuses on the population mean. If you create many random samples that are normally distributed and for each sample you calculate a confidence interval for the mean, then about 95% of those intervals will contain the true value of the population mean.

      The prediction interval focuses on the true y value for any set of x values. If you create many random samples that are normally distributed and for each sample you calculate a prediction interval for the y value corresponding to some set of x values, then about 95% of those intervals will contain the true y value.

      Charles

      Reply

  39. Hi, Charles. Can you make a video on plotting a 95% confidence interval. Above instruction was really confusing. Will be grateful.

    Reply

    • Ang,
      Thanks for your input. I will try to improve the explanation, but first I need to finish up the work I am doing on time series analysis.
      Charles

      Reply

  40. Hi Charles,
    I need like to plot the 95% Confidence Interval curves just like they are shown within Figure 1 (e.g. the dotted lines). How would you recommend doing this in Excel? I was informed that other programs may provide this feature, but I prefer to continue working in Excel if at all possible.
    Thank you in advance,
    Andy

    Reply

    • Yes, you can do this in Excel. E.g. to create the dotted line for the upper confidence interval curve, fill in a range of x and y values (say A1:B100) as follows: (1) in column A insert x values of the appropriate scale. If for example you are looking at values between 0 and 10, insert 0 in cell A1 and the formula =A1+.1 in cell A2 and then highlight the range A2:A100 and press Ctrl-D, in (2) in column B insert the y values for the upper confidence interval. E.g. in cell B1 insert the Excel formula for the upper confidence interval value corresponding to the x value in cell A1 (this is as described in cell E15 of Figure 2 of the referenced webpage), then highlight range B1:B100 and press Ctrl-D. (Make sure that you use absolute addressing for all the parts of the formula in B1 that don’t depend on the x value in cell A1.) (3) Finally, highlight range A1:B100 and select Insert > Charts|Scatter.
      Charles

      Reply

  41. Hi Charles,
    I wanted to point out a common misunderstanding about confidence intervals: CI’s say nothing about the probability that the true value of the population parameter lies within them – it either does or it doesn’t. A 95% CI just tells you that, if you were to repeat your experiment (sampling) an infinite number of times and run the statistics on each sample, the true parameter will lie within 95% of those confidence intervals. What you described as a CI in the first section of your post is actually Bayesian credible interval, which is a bit more complicated to calculate, but it does tell you the probability that your population parameter lies within the interval.
    Cheers,
    Phil

    Reply

    • Phil,

      Thanks for correcting my somewhat appealing, but, in the end, inaccurate statement. Shortly I will update the website with a more accurate characterization of the confidence interval.

      I appreciate your help in making the site more accurate.

      Charles

      Reply

  42. Hello! Thank you very much this incredibly helpful guide! Do you have a tutorial on how to find the C.I and P.I using multiple regression?

    Reply

  43. Hi Charles,
    I notice that you use n-2 for degrees of freedom, whilst other publications, for example UKAS M3003, use n-1. Although a small difference is seen in the calculation of the degrees of freedom, it can greatly affect the interval magnitude. Could you give some advise as to which calculation should be used for the df value? Thank you in advance for your reply.

    By the way, your website has been an extremely useful aid, Thanks

    Reply

    • Paul,
      I am not familiar with UKAS M3003, but I just checked a few other publications and they all show df = n-2 when calculating the confidence interval for regression.
      Charles

      Reply

  44. Charles,

    What’s the rationale for the added 1 under the square root of the standard error of the prediction? Theoretically, why 1?

    Thank you

    Reply

    • Ryan,
      The standard error for a prediction interval adds the variability of the points around the predicted mean. mathematically this is where the 1 comes from.
      I plan to eventually show the proofs of the formulas for the confidence and prediction intervals. You will then be able to see from the proofs more precisely where the 1 comes from.
      Charles

      Reply

  45. Hi Charles,

    This post has helped me so much already, really very insightful and easy to follow!

    I am trying to do a prediction interval for some metal fatigue test data but I am trying to find 90% confidence in the 98% reliability data. In order to do this is just using 0.1 as the probability in TINV sufficient for the method to change it to the 90% probability or do I need to make more changes please?

    Thanks for your help!

    Tristan

    Reply

    • Tristan,
      TINV(.1,df) (i.e. alpha = .1) is part of the formula for a 90% prediction interval. But I don’t understand what the 98% reliability data means.
      Charles

      Reply

  46. Hi all,

    It would be good to point out that the function TINV gives a two-sided confidence interval. The new function T.INV (with a dot) gives a one-sided confidence interval. In case of using the new function, you should take \alpha/2; furthermore, it uses the 1-\alpha/2 value, thus, T.INV(0.975,df).

    Emiel

    Reply

      • Hi Charles,

        Your post has been of tremendous help to me.
        Although it took me some time I have applied most of the solutions and they have worked just fine.
        I need clarification on example 2. Why did you have to eliminate the # 1 before 1/15?
        Would really appreciate your prompt response.
        Thanks.

        Reply

        • The test uses the confidence interval and not the prediction interval. This is why a 1 is not inserted before 1/15. Shortly I will update the webpage to explain better when the prediction interval is used and when the confidence interval is used.
          Charles

          Reply

  47. Hi Charles,
    I am using a exponential/hyperbolic function to fit my data. The model is (a*X+b)-SQRT[(a*X+b)^2-((4*a*X*b*c)/(2*c))].
    I wonder if I can calculate prediction intervals in the way you show, or if there is any parameter that is different for this type of models. If so, can you tell me how I should calculate it?
    Thank you very much
    Elisa

    Reply

  48. Hi Charles,

    Is Syx = Sres = STEYX(Y,X)? Is it same as Syx = SQRT((SUM(yi – Yi)^2)/(degrees of freedom)), where (xi,yi) are given data and Y is any nonlinear model (not a straight line, say a sigmoidal or logistic curve), which fits the data.

    Reply

    • Rizwan,
      Sorry for the long delay in responding to you. I just realized that I overlooked responding to you.
      It is true that Syx = Sres = STEYX(Y,X) = SQRT((SUM(yi – Yi)^2)/df) for linear models. I am not sure what these terms would even mean for non linear models such as logistic regression models.
      Charles

      Reply

  49. Hi Charles,

    Thanks for your contributions on this site. I’m a bit confused by your base formula, though. Where you use the sum of squared deviations of x (SSx, calculated as DEVSQ(x) or DEVSQ(A4:A:18), I’ve learned to use the standard deviation of x times (n-1), or STDEV.S(A4:A:18)*(n-1) in Excel speak. This would yield a value of CI SE of 2.090695467 and a PI SE of 8.244184143. The difference is small in your dataset, but where deviations are larger the use of sums of squared deviations instead of the method I’ve heard will yield very different results. That said, I’m not at all certain which method is correct–can you point to some references for your formula, please?

    Thanks in advance for taking the time to clarify this issue for me.

    David

    Reply

    • Hi David,

      Note that for any range R1, the square root of DEVSQ(R1) is STDEV.S(R1)*(n-1). In fact, in the formula for cell E12 in Figure 2 of the referenced page I do take the square root of SSx, and so it seems that we should get the same answer. Can you send me an example of your calculation so that I can see why the results are not the same?

      Charles

      Reply

Leave a Comment