Characteristics of a binomial distribution
Definition 1: Suppose an experiment has the following characteristics:
- the experiment consists of n independent trials, each with two mutually exclusive possible outcomes (which we will call success and failure)
- for each trial, the probability of success is p (and so the probability of failure is 1 – p)
Each such trial is called a Bernoulli trial. Let x be the discrete random variable whose value is the number of successes in n trials. Then the probability distribution function for x is called the binomial distribution, B(n, p), whose frequency function (aka probability density function) is
f(x) = C(n, x)px(1–p)n–x
where C(n, x) = and n! = n(n–1)(n–2)⋯3∙2∙1 as described in Combinatorial Functions.
C(n, x) can be calculated by using the Excel function COMBIN(n,x). See Figure 2 of Built-in Excel Functions for more details about this function.
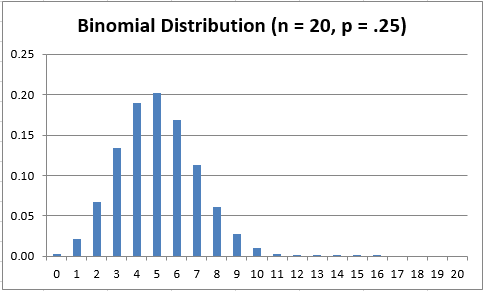
Figure 1 shows a graph of the probability density function for B(20, .25).
Figure 1 Binomial distribution
That the graph looks a lot like the normal distribution is not a coincidence (see Relationship between Binomial and Normal Distributions)
Mean and Variance
Property 1:
Mean = np
Var = np(1–p)
Click here for a proof of Property 1.
Excel Worksheet Functions
Excel provides the following functions regarding the binomial distribution:
BINOM.DIST(x, n, p, cum) = the probability density function value f(x) for the binomial distribution (i.e. the probability that there are x successes in n trials where the probability of success on any trial is B(n, p) when cum = FALSE and the corresponding cumulative probability distribution value F(x) (i.e. the probability that there are at most x successes in n trials where the probability of success on any trial is p) when cum = TRUE.
BINOM.INV(n, p, 1 – α) = critical value; i.e. the smallest value of x such that F(x) ≥ 1 – α, where F is the cumulative binomial distribution function for B(n, p)
These functions are not supported for versions of Excel prior to Excel 2010; the following functions are used instead: BINOMDIST, which is equivalent to BINOM.DIST, and CRITBINOM, which is equivalent to BINOM.INV.
Excel 2013 introduces the following new function (where x ≤ y ≤ n):
BINOM.DIST.RANGE(n, p, x, y) = the probability there are between x and y successes (inclusive) in n trials where the probability of success on any single trial is p
Thus, BINOM.DIST.RANGE(n, p, x, y) = BINOM.DIST(y, n, p, TRUE) – BINOM.DIST(x–1, n, p, TRUE) if x > 0 and BINOM.DIST.RANGE(n, p, 0, y) = BINOM.DIST(y, n, p, TRUE). The y parameter may be omitted, in which case BINOM.DIST.RANGE(n, p, x) = BINOM.DIST(x, n, p, FALSE).
Examples
Example 1: What is the probability that when you throw a die 10 times it will come up six 4 times?
We can model this problem using the binomial distribution B(10, 1/6) as follows
Alternatively, the problem can be solved using the Excel formula:
BINOM.DIST(4, 10, 1/6, FALSE) = 0.054266
Example 2: What is the probability that heads come up more than tails in 20 tosses of a fair coin?
Let E1 = the event that heads come up more than tails, E2 = the event that tails come up more than heads, and E3 = the event that heads comes up just as many times as tails. First note that P(E1) = P(E2) and P(E1) + P(E2) + P(E3) = 1, and so P(E1) = (1–P(E3))/2. Now
![]()
Critical values of a discrete distribution
Because the binomial distribution is discrete, the values calculated by BINOM.INV (or CRITBINOM) may not always represent the critical values. E.g. suppose you are conducting a two-tailed test with n = 100, p = .4 and α = .05, then BINOM.INV(100, .4, .025) = 31. But note that
BINOM.DIST(31,100,0.4,TRUE) = .03985
BINOM.DIST(30,100,0.4,TRUE) = .02478
Since .02478 ≤ .025 = α/2, the lower critical value is 30 and not 31. In fact, the lower critical value is always 1 less than the value calculated by BINOM.INV, except in the case where the value is calculated by =BINOM.DIST(x, n, p, TRUE) is exactly α/2, in which case, x = BINOM.INV(n, p, α/2); and so, in this case, you shouldn’t subtract 1.
It turns out that the upper critical value is indeed the one calculated by BINOM.INV. In the example given above, BINOM.INV(100, .4, .975) = 50 and
BINOM.DIST(50,100,0.4,TRUE) = .9832
BINOM.DIST(49,100,0.4,TRUE) = .9729
Since .9832 ≥ .975 = 1 – α/2, but .9729 < .975, the critical value is in fact 50.
Real Statistics Function
The Real Statistics Resource Pack provides the following function that implements the above process to identify the appropriate critical value.
BINOM_CRIT(n, p, α): if α < .5 then the left critical value is returned, while if α ≥ .5, then the right critical value is returned.
If you are employing a two-tailed test, then you must substitute α/2 for α to get the left critical value and substitute 1–α/2 for α to get the right critical value.
For the previous example given above, we get BINOM_CRIT(100,.4,.025) = 30 and BINOM_CRIT(100,.4,.975) = 50.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Forbes, C. Evans, M, Hastings, N., Peacock, B. (2011) Statistical distributions. 4th Ed, Wiley
https://www.wiley.com/en-us/Statistical+Distributions%2C+4th+Edition-p-9780470390634
Wikipedia (2012) Binomial distribution
https://en.wikipedia.org/wiki/Binomial_distribution
How many minimum number of people would have to visit the store to give you at least a 0.95 probability of covering the transportation costs and the additional fee? Use as 0.28 the probability of a widget being selected by a person.
HINT: You need to sell at least 40 widgets to cover transportation cost and the additional fee. So the number of “successes” need to be greater than equal to 40. The probability of “success” in each trial is 0.28. Now use the BINOM.DIST function trying out various values for “n”, the number of trials.
how it will solve?
What sort of problem are you having in trying to do this homework problem?
Charles
Hi, can someone please help me with this:
Chocolate operations are carried out on two separate production lines, one driven by a new machine and the other by a relatively older machine. Recent monitoring of each machine show that the probability of failure in the new one is 0.2% and the old one is 0.8%. Given that the quality assurance department insists on a probability of 99.9999% that at least one machine is working at all times. Advise the company if this condition is being satisfied.
There’s no trial data and no other data. So I’m not sure how to proceed. I’m very confused.
Jessica,
Do you know how to find the probability that both fail?
Charles
Hi Charles, no I don’t. Is there a specific formula I can use?
Jessica,
What is the probability that the older machine fails?
What is the probability that the newer machine fails?
Charles
The new machine is 0.2% and the old machine is 0.8%
Jessica,
Now, what is the probability that both machines fail at the same time?
Charles
100%?
No. It looks like you need to go back and review some basic probability theory, See
https://www.real-statistics.com/basic-probability-concepts/
Charles
thank you for the explanation, this was very well written
Suneil,
Thank you for your kind words.
Charles
Hi, Could anyone help me with solving that exercise?
Assume that the your_data is in fact binomially distributed with n=10 and with probability of success equal to 0.5. Using such a binomial distribution find the probability that the number of successes in 10 trials is equal to i) first value in your data; ii) first value in your_data plus 1 iii) first value in your_data minus 1. Now, approximate those probabilities using normal distribution and show your work explicitly i.e. how did you get the results? Approximate the same probabilities with Poisson distribution. What are the conditions to apply those approximations?
Javidan,
I am sorry, but I prefer not to directly answer questions that are likely to be from a homework assignment.
What sort of difficulty are you having in answering question (i)?
Charles
Hello Charles,
Need some help with the following problem
“Here we look at a more generic example such as coin flipping. There is a sequence of trials where each trial is a success with probability p and a failure with probability 1 − p. A run is a sequence of consecutive successes or failures. For most of us, intuition says that there should not be long runs. Test this by finding the probability that there is at least one run of length at least six in a sequence of 15 trials. (The run could be of 0s or 1s.) You can use any value of p you like—or try different values of p.”
Thanks
See Runs
Charles
Hi Charles,
I’m a total amateur at excel and binomial distribution. I’ve been given a question as part of my food science studies that I wonder if you could help me enter into excel and work out.
Question, Your company has put 200 prizes into 10,000 packs of food. Use the binomial theorem to find the probability of getting 1 prize if you were to buy 4 of the food packs?
Many thanks in advance
Stephen,
This is similar to Example 1. If you select one food pack at random, what is the probability of getting a prize?
Charles
Hi there! can anyone help me with these?
“You have been given a new multiple choice quiz, on this quiz there are 10 questions. Every question is multiple choice with 3 options, and only one of those options is correct. What is the probability you get 3 questions correct?” I would use the Binom.dist in Excel
or this one “the number of puppies that get adopted from the humane society of greater Waukesha county is modeled with a Poisson distribution, with an average of 6 puppies adopted weekly.” I would these poisson.dist in excel.
Guinevere,
Yes, you use the binomial and Poisson distributions for these examples. For the first example since there are three choices for each question, p = 1/3.
Charles
can anyone help me on this? Fatal pedestrian accidents (peopling walking that get killed by cars) occur about 1.6 times each month in a large city. These accidents are typically unrelated and involve a person walking by themselves. Make a probability distribution for the number of fatal pedestrian accidents per month (use a column graph).
Do you have any other data? What distribution do you think data showing the number of fatal pedestrian accidents per month would follow?
Charles
Use Excel functions to complete each of the following Biostatistics problems.
Problem 1 – Binomial Distribution
Use the following data on Mendel’s pea plants to find the probability that exactly two of the ten trials will be successful. Notes:
1. “Successful” is defined as a yellow pod.
2. The probability of success on each trial is 0.25, and each trial is done with a monohybrid cross.
3. Green pods are dominant over yellow pods.
Plant # Pod color
1 yellow
2 green
3 green
4 green
5 green
6 green
7 yellow
8 green
9 green
10 green
Problem 2 – Poisson Use the data & information from Problem 1 to find the Cumulative Poisson probability for the values.
Soraya,
What is your question or comment?
The Binomial Distribution and Poisson Distribution webpages on the Real Statistic website show how to do these two problems.
Charles
The probability that a body builder will have two protein bars as a mid-morning snack is 0.6. The probability of having three protein bars as an afternoon snack is 0.8. They only eat protein bars at those times each day.
a Show that the probability the body builder will eat at least two protein bars on any one day is 0.92. (Hint: Draw a tree diagram to show all the possible outcomes and probabilities).
b What is the probability they will eat at least two protein bars on at least five of the seven days in a week?
c Which of these two calculations could be found using the binomial distribution and why is it an appropriate model to use?
Give two reasons why it is, and one reason why the other calculation could not use the binomial distribution.
Zurtasha,
What sort of help do you need?
Charles
I need help in part a b and c. Please
Yes, but can you ask some specific questions about the specific issues that you don’t understand or are having difficulty with.
Charles
1.A box contains 18 balls. Six are black and 12 are white.
A sample of four balls is taken with replacement.
aWrite down the binomial distribution
What do you think “success” is for this scenario?
Charles
The 6 black balls out of 18
Hello Zurtasha,
I don’t understand.
Charles
The answer to a is: \binom{n}{k}p^{k}(1-p)^{(n-k)}
I have questions on
A normal distribution has a mean of 80 and a variance 25. if a value is taken at random, what is the probability that it is
1.greater than 80,
2.less than 74.8,
3. within 14.7 of 80,
4.between 73.6 and 83.6
Hello Shradha,
The Excel function =NORM.DIST(x,m,s,TRUE) gives the probability that the random value is less than x for normally distributed data from a normal distribution with mean m and standard deviation s. Since a variance of 25 means that the standard deviation is 5, the answer to item #2 can be found using the formula =NORM.DIST(74.8,80,5,TRUE).
I’ll let you figure out the answers to the other items.
Charles
48. True or False. The binomial distribution is best for modeling the number of successes in a binomial or Normal setting . A) True B) False
hi,
I would appreciate if anyone could help me with calculation of LOSS FUNCTION for binomial distribution in EXCEL
for example for Poisson:
Loss(r) = 𝜇 * poisson.dist (r+1, 𝜇 , 0) – (r+1- 𝜇)*(1- poisson.dist (r+1, 𝜇 , 1)
Hello Shiry,
The Real Statistics website doesn’t yet handle this topic. Perhaps the following webpage would be helpful. Alternatively, perhaps someone else in the community will address your comment.
https://m.tau.ac.il/~mansour/ml-course-02/ml2.ppt
Charles
Tnx!
Analyze the excel sheet formula and identify which that does not belong to the group
Select one:
a. f(x)=NEGBINOM.DIST(12,6,0.5,FALSE)
b. f(x)=EXPON.DIST(9,1/10,FALSE)
c. f(x)=NORM.DIST(183,175,E9,FALSE)
d. f(x)=BINOM.DIST(5,10,0.5,FALSE)
I could probably make a case for any one of the answers. Are all the formulas correctly stated?
Charles
Hello Charles,
I have the basic doubt on how to decide if the last parameter of BINOM.DIST would take up a True/False value. For example in the question In the game of roulette, a steel ball is rolled onto a wheel that contains 18 red, 18 black, and 2 green slots. If the ball is rolled 25 times, find the probability of:
The ball falls into red slots less than 11 times
Here is the parameter TRUE?
Yes, you would use TRUE
Charles
Of great interest is the probability of the number of binomial successes
EQUAL TO OR GREATER than some number.
For example, for a fair coin, in N=20 flips, what is P(15 or more heads,
or 5 or less heads). I do not see that function in Excel, although
BINOM.DIST.RANGE will calculate that for 15 heads, 16, etc, and those
individual P values can be be summed for the total probability.
Perhaps there is a function in Excel that does that, but I did not find it.
Hello Garry,
P(15 or more heads) = 1-BINOM.DIST(14,20,.5,TRUE)
P(5 or less heads) = BONOM.DIST(5,20,.5,TRUE)
P(15 or more heads, or 5 or less heads) = 1-BINOM.DIST(14,20,.5,TRUE) + BONOM.DIST(5,20,.5,TRUE)
Charles
Hi,
How can we use Excel macros to generate binomial operating curves? If we give n and c and p as input we may generate the operating curves of fraction defective vs the probability of acceptance?
Gautam,
What do you mean by “binomial operating curves”?
Charles
Thank you, this really helped me a lot.
Please tell me the similarities and differences between normal distribution, sampling distribution and binomial distribution??
See the following webpages:
https://real-statistics.com/sampling-distributions/central-limit-theorem/
https://real-statistics.com/binomial-and-related-distributions/relationship-binomial-and-normal-distributions/
Charles
Hello,
Kindly guide me on these questions
Binomial Distribution Problem 1:
(a) An urn contains 1000 balls, 100 are green and 900 are white. One ball is chosen
from the urn 100 times with replacement. Use Excel (binom.dist) to find the probability
that six or seven green balls are selected.
(b) An urn contains 1000 balls, 100 are green and 900 are white. One ball is chosen
from the urn 1000 times. Use Excel (binom.dist) to find the probability that between 110
and 120 of the balls, inclusive, are green.
(c) Redo (a) and (b) again using Excel but use the normal approximation (normal.dist).
How do the answers compare with the above. Are there any discrepancies? If so,
please explain why they happened.
Hypergeometric Distribution. Problem 2:
(a) An urn contains 1000 balls, 100 are green and 900 are white. One ball is chosen
from the urn 100 times without replacement. Use Excel (hypgeom.dist) to find the
probability that six or seven green balls are selected. How does this compare with the
answer in 1(a)?
(b) An urn contains 1000 balls, 100 are green and 900 are white. One ball is chosen
from the urn 1000 times. Find the probability that between 110 and 120 of the balls,
inclusive, are green. OK, this is silly, since we know the answer. This really has no
relation to 2(b), since the probability is 0.
Obviously, the hypergeometric distribution can be quite different from the binomial
distribution.
(c) An urn contains 1000 balls, 100 are green and 900 are white. One ball is chosen
from the urn
1000 times. Find the probability that between 80 and 85 of the balls, inclusive, are
green. Compare the answers when the sample is performed with and without
replacement.
Note: It used to be common practice to use the binomial distribution as an
approximation of the hypergeometric distribution. This practice is no longer necessary in
many cases due to the computation power available to nearly anyone with a computer.
Rose,
The examples using the binomial distribution are similar to Example 1 on the Binomial Distribution webpage
The hypergeometric examples are similar to those found at
https://real-statistics.com/binomial-and-related-distributions/hypergeometric-distribution/
The normal approximation can be found at
https://real-statistics.com/binomial-and-related-distributions/relationship-binomial-and-normal-distributions/
Charles
1) Binomial Distribution
Experiment: Flip 5 fair coins at the same time and count the total number of head.
Mean = 2.5
Variance = 1.25
Repeat 100 times, record the results.
Head = 1
Tail = 0
Question: Describe the shapes of the distribution (pmf) in the experiments of Binomial and Geometric. Explain for each graph, why the graph has this shape and pmf?
2)Geometric Distribution
Experiment: Flip 3 coins at the same time. Record the total number of tosses until you get all heads or tails.
Mean = 4
Variance = 12
Repeat 100 times, record the results.
# of tosses until all heads or tails
(Record 15 if the number > 15.)
Question : Why the Geometric distributions have these shapes and pmf?
Sam,
What do you believe the answers to these questions are?
Charles
i am not too sure about the answer.
i understand the experiment for tossing a coin. However i want to understand why flipping multiple coins will lead to a binomial histogram
Sam,
If say you toss 5 coins, then on any one toss, the probability of any particular toss is as follows (using a binomial distribution):
5 heads 1/32
4 heads 5/32
3 heads 10/32
2 heads 10/32
1 head 5/32
0 heads 1/32
If you toss the same 5 coins 32,000 times, then on average you would expect the following numbers for each possibility (the law of large numbers)
5 heads 1,000
4 heads 5,000
3 heads 10,000
2 heads 10,000
1 head 5,000
0 heads 1,000
Of course, in actual fact, the distribution won’t be exactly this, but it will be similar in shape (i.e. the histogram will be similar).
Charles
thanks for the explanation ! (:
Question for CASE STUDY 1
The number of credit card holders of a bank in two different cities (city – X and city – Y) settling their excess withdrawal amounts in time without attracting interest follows binomial distribution. The manager (collections) of the bank feels that the proportion of the number of such credit card holders in the city – X is not different from the proportion of the number of such credit card holders in the city – Y. to test his intuition, a sample of 200 credit card holders is taken from the city – X and it is found that 160 of them are settling their excess withdrawal amount in – time without attracting interest. Similarly a sample of 180 credit card holders is taken from the city – Y and it is found that 50 of them are settling their excess withdrawal amount in – time without attracting interest, check the intuition of the sales manager at a significance level of 0.05.
Donsah,
This looks like a classroom assignment. What do you think is a good approach for solving this problem?
Charles
can I get a solution?
A solution to what?
Charles
any solution?
Donsah,
I don’t know what you are referring to.
Charles
can anyone solve the above case study?
Donsah,
The solution is very similar to that for Example 1 on the following webpage:
https://real-statistics.com/binomial-and-related-distributions/proportion-distribution/
Charles
Hello
I am interested in this problem.
The success probability is 90% for a radar machin. If I instal 2 radar machines what is the new success probability, if I install 3 radar machines, what is the success probability .
Sincerely
Wilson,
If the machines are independent, then the probability of success for each machine is still 90%. The probability of success on 2 or 3 machines depends on what you mean by success. If you mean that at least one machine succeeds then the probability all failures with n machines is (1-.9)^n, and so the probability that at least one machine succeeds is 1-(1-.9)^n.
Charles
Hi Charles,
I have the following problem. Consider an event (e.g. being invited for an interview) occurring with probability q in the sense that for every 1000 applications sent, 1000*q lead to an invitation. Now say 30 such applications have been sent, and this resulted in 3 interviews. The probability of this occurring is according to the binomial distribution C(30,3)*q^3*(1-q)^27.
Consider now another candidate (with a different CV) who has a probability of r of being invited. He sends 50 applications and receives 1 interview. The probability of this happening is C(50,1)*r*(1-r)^49.
The probability of both events happening is, of course, p({3/30,1/50}|{q,r}) = C(30,3)*q^3*(1-q)^27 * C(50,1)*r*(1-r)^49.
How would you go about calculating the probability that q > r from this data? I am effectively interested in the reverse of the above, namely p(q>r|{3/30,1/50}) Alternatively, in terms of hypothesis testing, if H0 = (q<=r), what is the p-value for rejecting the null hypothesis?
Cristian
In a lot of 200 units of microchips, 15 are defective. Suppose that 25 items are selected. Use EXCEL
(HYPERGEOM.DIST) to find the probability that between 5 to 10 of the items are defective
John, see my response to your previous comment.
Charles
In a lot of 200 units of microchips, 15 are defective. Suppose that 25 items are selected. Use EXCEL
(HYPERGEOM.DIST) to find the probability that 5 or 6 defective items are selected.
John: Hint what is the relationship between the hypergeometric distribution and the binomial distribution?
Charles
In a lot of 200 units of microchips, 15 are defective. One chip is chosen, 25 times with replacement.
Use EXCEL (BINOM.DIST) to find the probability that between 5 to 10 of the items are defective
John,
Hint: The probability of between 5 and 10 defects is equal to the probability of less than 11 defects minus the probability of less than 5 defects.
Charles
How would I got about trying to solve this in EXCEL?
“In a lot of 200 units of microchips, 15 are defective. One chip is chosen, 25 times with replacement. Use excel (binom.dist) to find probability that 5 or 6 defective items are selected.”
John,
How to solve this problem is explained on the referenced webpage. Here is a hint: p = 15/200 = probability of choosing a defective chip when one chip is selected at random.
Charles
The Binomial formula in Excel requires a sample size. Can this formula be used to find the sample size when it is unknown but Reliability and Confidence are known and number of failures is not one? Otherwise, when number of failure is 0, the formula to find sample size is:
ln (1-c)/ln r.
Fred,
What reliability and confidence statistics are you referring to?
Charles
Excellent explanations, and comprehensive.
Typo in sentence just above Figure 1. … B(10, .25) should be B(20, .25)
Joe,
Glad you found it useful and thanks for identifying this typo. I have now corrected the mistake.
I appreciate your help in making the website more accurate.
Charles
Hello,
Thank you for your informative posts. I am trying to create a calculator for sample size from first principles and am having difficulty isolating for sample size (n) with the Binomial functions. Is there a way in excel to calculate the required sample size (n) given: confidence level (c), reliability (r), and number of expected failures (x)? e.g. 90% reliability with 95% confidence; sample testing has 3 failures so sample size must be n?
Thank you for your help.
Katie,
What do you mean by reliability (r)?
Charles
Hi Charles,
Thanks for your response. What I meant in terms of reliability was the probability of success. Using the first principles formula and the Solver functionality in Excel/VBA, I was able to program a numerical solution for any of the unknowns, given the other three.
Thanks again,
Katie
There is a flight from city A to city B and the aircraft for this flight has 40 seats for customers. One ticket can be sold for £1K. So, if the company sells 40 tickets, the revenue is £40K. There is only fixed and sunk cost; the cost for this flight is the same regardless of how many passengers there actually are. Also, statistics shows that each person who purchased a ticket independently shows up with probability 0.72. Therefore, there is possibility that the company can earn more money by overbooking tickets. For example, if the company sells 42 tickets, the sales will be £42K, and there won’t be any problem if no more than 40 purchasers actually show up. However, the company has a policy that any customer who cannot take the flight due to ‘overflow’ should be given an alternative plane ticket as well as monetary compensation. The cost for this is £2K. That is, if the company sells 42 tickets and all the 42 purchasers actually turn up, two persons cannot take the flight, so the net revenue will be £42K sales minus £4K compensation, that is, £38K. Answer the following questions.
What is the net-revenue-maximising number of tickets to sell?
How would I compute this on excel solver and what would be the constraints?
Cameron,
Several people have now asked the exact same question and so I am going to assume that this is a homework problem, which I generally don’t answer. Instead I will give some hints:
1. Re maximizing revenues, you should calculate the expectation of x where x = the revenues and then maximize this value.
2. To find the maximum, you can use calculus or Solver. The calculation using Solver comes from hint #1 above. The only constraint that I can think of is that the number of seats is 40.
Charles
Can you explain me what difference between chi-square test and binomial distribution test.
If I using them to data (2 answer : Yes ,No)
In 2 alternate force choice
What be better?
Thank you so much
Each one is described on the website and can be used for different types of anayses. Which is better depends on the specific nature of the analysis you want to conduct. You have not supplied enough inofrmation for me to be able to tell you which is better for your analysis.
Charles
53% of American households subscribe to cable TV. You randomly select six households and ask each if they subscribe to cable TV. Construct a probability distribution for the random variable, x. Then draw the histogram and a pie chart showing the relative frequency distribution of the data using (use Microsoft excel) show all the working plizzzzzzzzzzzzzzzzzzzz. i need to u8nderstand it
I have a problem where there are X amount people who are willing to buy a higher priced airline ticket, and 20% of those X will buy a lower priced ticket if there is one available. If I know how many low priced seats are available, can I use the binom.dist function to give me a random draw of how many of those seats will be taken by the higher paying customers? I’m running a simulation so I don’t want to just use 20% * number of low priced tickets. Thanks.
Jack,
I know that you can use the binomial distribution for similar type problems, but I don’t have enough information to judge in your case.
Charles
Charles,
I have a system which is specified to perform to a certain probability of success. It can only pass or fail thus a binomial probability. I need to design a series of tests with the minimum n to determine if the demonstrated results indicate that true performance is greater than or equal to the specified value. You can assume the tests are independent. The test results must have a specific confidence associated with it. I have used the following formula ”=1-BINOMDIST(# of failures, # of trials, 1-probability of success, cumulative) and more or less thru trial and error played around with the number of trials in order to achieve a probability which gets me the required confidence.
My question is three fold. 1. Is there a more elegant way to find n for given confidence levels? 2. If I believe that true performance is going to be less than the specified performance I would like to determine what my sample size should be to determine that there is no likelihood that it was going to approach the specified threshold. This way I can construct the test in such a way as to minimize the cost to stop the test if it is going to be determined that it is not going to result in meeting the threshold. What would I use in excel to do this? A negative binomial function? 3. Lastly how many runs (n) would I require in order to estimate what the true performance of the system is with confidence and how would that look in excel?
Jamey,
1. Before I can answer your question, what is n? Is it the smallest number of trials that yields a given number of successes x based on a constant probability of success on any single trial p? If so this can be found using the negative binomial distribution.
2. I don’t completely understand this question.
3. Is this n the same as the n in question 1? Also, I don’t know what you mean by performance.
One last point, when you need to iterate to a solution via trial and error (as you seem to have done), then you can often accomplish the same thing by using Excel’s Goal Seek or Solver capability.
Charles
can u answer this for me plis P(z<-1.5)
Does z have a standard normal distribution? If so, P(z < -1.5) = NORM.S.DIST(-1.5, TRUE) = .0668. Charles
P(z1.5) = 1-p(z<1.5)
1 – NORM.S.DIST(1.5, TRUE)
Assume that 96% of ticket holders show up for an airline flight. If a plane seats 200 people, how many tickets should be sold to make the chance of an overbooked flight (more ticket holders show up for a flight than there are seats available) is at most 10%.
Please help me here.
I think its 213 , is that appropriate?
David,
How did you arrive at the answer of 213?
Charles
By trial and Error method. Not sure if there is a different method to solve this case. Please advise.
David,
The probability that at most 200 seats will be filled from 200+x tickets sold is =BINOM.DIST(200,200+x,0.96,TRUE). This is the probability that the flight is not overbooked. Presumably you are looking for the largest value of x such that this probability is more than 90%.
If x = 5 this probability is 91.6%. If x = 6 this probability is 83.5%. Thus the answer is 205 seats.
Charles
Hi Charles
Your willingness to respond with solutions in various fields is admirable, and generous.
My problem is in trading derivatives, specifically to find the probability of experiencing at least 1 sequence of k consecutive failures occurring in N trades. The probability of a win is P and a loss (1-P), Bernoulli distribution appears to be applicable. I have listed by hand the 2^N combinations for N=5. The approach used is to identify from the table the combinations where for example the k =2 consecutive losses do not appear. Each combination has a probability of occurrence, for example P=0.6 and combination WLWWL probability =0.6*0.4*0.6*0.6*0.4. Sum all the probabilities of the combinations identified and subtract from 1.0 to find the answer. This approach was used to check the results found by Excel
+1.0-BINOMDIST(0,N-k+1,(1-P)^k, FALSE). The by hand results are around 20% lower than the Excel formula results. The real world problem would be to find answers for say N=60 and k=5, which would be totally impractical to do by hand (2^60 combinations!), so a formula approach is required.
Your comments would be appreciated.
Regards
Chris
Chris,
This sounds like the type of problem that I addressed on the following webpage:
https://real-statistics.com/binomial-and-related-distributions/runs/
Charles
Hi,
I have a problem as follows:
2. You run a local airline company. There is a flight from city A to city B and the aircraft for this flight has 30 seats for customers. One ticket can be sold for £1K. So, if the company sells 30 tickets, the revenue is £30K. There is only fixed and sunk cost; the cost for this flight is the same regardless of how many passengers there actually are. Also, statistics shows that each person who purchased a ticket independently shows up with probability 0.75. Therefore, there is possibility that the company can earn more money by overbooking tickets. For example, if the company sells 32 tickets, the sales will be £32K, and there won’t be any problem if no more than 30 purchasers actually show up. However, the company has a policy that any customer who cannot take the flight due to ‘overflow’ should be given an alternative plane ticket as well as monetary compensation. The cost for this is £2K. That is, if the company sells 32 tickets and all the 32 purchasers actually turn up, two persons cannot take the flight, so the net revenue will be £32K sales minus £4K compensation, that is, £28K. Answer the following questions.
(a) If the company sells 35 tickets, what are the company’s net revenues if exactly (i) 29, (ii) 31, or (iii) 33 people show up, respectively? (b) If the company sells 35 tickets, what is (i) the probability of no more than 30 people showing up, (ii) the probability of exactly 31 people showing up, and (iii) the probability of exactly 33 people showing up? (c) Compute and report the expected net revenue from selling 35 tickets. (d) What is the net-revenue-maximising number of tickets to sell? Report the number of tickets to sell and the achieved net revenue.
I have used your information (which was brilliant) to answer questions a) and b) but I was wondering if I can use the same maths here to answer c) and d) as I can’t figure out how to apply it to those questions.
Many thanks
Just to add to that, I have done part c) in excel using 35000 – bin.dist(35,35,0.75,false)*(10000)-bin.dist(34,35,0.75,false)… etc down to 31.
I’d like to do this to find out the expected values for when more than 35 tickets are sold as I think the revenue maximising tickets sold will be higher maybe around 40 or 41 but excel won’t allow me to use the same binomial formula as I did in part c) possibly because it can’t exceed 35 tickets.
Hi Danielle,
The answer for (c) is 35000 – bin.dist(35,35,0.75,false)*10000-bin.dist(34,35,0.75,false)*8000-bin.dist(33,35,0.75,false)*6000-bin.dist(32,35,0.75,false)*4000-bin.dist(31,35,0.75,false)*2000.
In general, if there are n extra tickets sold, then the net revenue is
3000 + n*1000 – bin.dist(n,n,0.75,false)*2000*n – bin.dist(n-1,n,0.75,false)*2000*(n-1) – bin.dist(n-2,n,0.75,false)*2000*(n-2) – … – bin.dist(31,n,0.75,false)*2000
You should be able to maximize this value by using Excel’s Solver. It may also be possible to simplify this expression mathematically and use calculus to find the maximum value.
Charles
If i will like to use solver to find max, what will be the constraints?
Elliot,
Sorry, but you need to provide more information. max of what_
Charles
Charles,
He means the maximum net revenue.
I have gone along with your suggestion for part d) however am having difficulties because theoretically ‘n’ could be any number, so your ‘…’ in your equation is giving me problems.
Ben,
I don’t know who you are referring to not what part d) means.
Charles
Hi Charles,
What would be the constraints in order to maximise the net revenue on Excel Solver? How would this be done?
Thanks,
Isobel
Isobel,
Sorry, but you haven’t provided enough information about your problem for me to be able to provide you with a response.
Charles
Hi again,
Wouldn’t c) be the bin.dist(35,35,0.75,false)*10000-bin.dist(34,35,0.75,false)*8000-bin.dist(33,35,0.75,false)*6000-bin.dist(32,35,0.75,false)*4000-bin.dist(31,35,0.75,false)*2000, but all the way down to zero, if not, why is this?
Thanks,
Isobel
Sorry Isobel, but I don’t see an c) on the referenced webpage and so I don’t know what you are referring to.
Charles
Hi Charles, for the comment above, what would be the constraints that you would suggest to use to find the net-revenue-maximising number of tickets to sell?
(the question posted above was:
Danielle says:
December 2, 2015 at 9:34 pm
Hi,
I have a problem as follows:
2. You run a local airline company. There is a flight from city A to city B and the aircraft for this flight has 30 seats for customers. One ticket can be sold for £1K. So, if the company sells 30 tickets, the revenue is £30K. There is only fixed and sunk cost; the cost for this flight is the same regardless of how many passengers there actually are. Also, statistics shows that each person who purchased a ticket independently shows up with probability 0.75. Therefore, there is possibility that the company can earn more money by overbooking tickets. For example, if the company sells 32 tickets, the sales will be £32K, and there won’t be any problem if no more than 30 purchasers actually show up. However, the company has a policy that any customer who cannot take the flight due to ‘overflow’ should be given an alternative plane ticket as well as monetary compensation. The cost for this is £2K. That is, if the company sells 32 tickets and all the 32 purchasers actually turn up, two persons cannot take the flight, so the net revenue will be £32K sales minus £4K compensation, that is, £28K. Answer the following questions.
(a) If the company sells 35 tickets, what are the company’s net revenues if exactly (i) 29, (ii) 31, or (iii) 33 people show up, respectively? (b) If the company sells 35 tickets, what is (i) the probability of no more than 30 people showing up, (ii) the probability of exactly 31 people showing up, and (iii) the probability of exactly 33 people showing up? (c) Compute and report the expected net revenue from selling 35 tickets. (d) What is the net-revenue-maximising number of tickets to sell? Report the number of tickets to sell and the achieved net revenue.
I have used your information (which was brilliant) to answer questions a) and b) but I was wondering if I can use the same maths here to answer c) and d) as I can’t figure out how to apply it to those questions.
Many thanks)
Thank you!
Shaz,
Several people have now asked the exact same question and so I am going to assume that this is a homework problem, which I generally don’t answer. Instead I will give some hints:
1. Re maximizing revenues, you should calculate the expectation of x where x = the revenues and then maximize this value.
2. To find the maximum, you can use calculus or Solver. The calculation using Solver comes from hint #1 above. The only constraint that I can think of is that the number of seats is 30.
Charles
Hi,
I’ve been measuring how long visitors to a zoo spend at exhibits and have a large data set of demographic information about the individuals and then various time data for each locations where they stopped to look at the animals. The time spent at the animals appears to follow a negative bionomial distribution so I want to analyse it using a generalized linear model comparing different types of visitor (age, gender etc). If I consider my data as counts of number of seconds someone stays at a location until they leave then the negative bionomial model seems to fit but I’m concerned that the probability of them leaving the location (probability of ‘failure’) is not a constant. The probability that they will leave presumably increases over time so is negative binomial the wrong regression in this instance?
Thanks
Duncan,
If I understand the scenario correctly, I believe that your model views “failure” in any specific unit of time as “remaining with the animals” and “success” as “leaving”. If the probability of leaving is constant then you you could use a negative binomial distribution. This is not possible if this probability is not constant. An example of a distribution where this probability is not constant is the hypergeometric distribution.
Charles
question.
binomial distribution
expected value is given = 4
n = 10
x = 7
cum = TRUE
what do I do to find probability using excel?
James,
The expected value for the binomial distribution is np. Since n = 10 and np = 4, it follows that p = .4. To find the cumulative probability of x, you use the formula =BINOM.DIST(x,n,p,cum), which in this case is =BINOM.DIST(7,10,.4,TRUE). If you are using a version of Excel prior to Excel 2010, then the formula is =BINOMDIST(7,10,.4,TRUE).
Charles
I have a binom.inv question.. Lets say
Q. 3 percent of parts created in a factory do not conform and must be reworked. John needs 100 good parts to ship. How many parts should he produce (considering the expected bad parts) to have a 95% chance of getting 100 good parts?
How to work this in binom.inv? Please help!
Misty,
Here are two ways of solving the problem, neither of which uses BINOM.INV.
Method 1. Consider “success” as getting a defective part. What is the probability of getting x defective parts in 100+x trials where the probability of success is 1-.97 = .03? The answer is BINOM.DIST(x,100+x,.03,TRUE). The values for x = 0 through 8 are
x Prob
0 0.047552508
1 0.190210032
2 0.40633618
3 0.626784852
4 0.79708145
5 0.903346528
6 0.959135694
7 0.984479915
8 0.994649283
You see that you need 6 “successes” to achieve more than 95% probability. This is equivalent to 106 trials
Method 2: Use the inverse of the negative binomial distribution. Excel provides the NEGBINOM.DIST function, but no NEGBINOM.INV function. Instead we use the Real Statistics NEGBINOM_INV inverse negative binomial function. The answer to the problem can be calculated via =NEGBINOM_INV(0.95,100,0.97), which has value 6. The answer once again is 106.
Charles
Hi,
i have a question, if i have a set of data:
Daily weight distribution bags :
2000 weight data per day
and i need to do a analysis on success weight and failure weight for a month. can i use binomial?
Hi,
Sorry, but I don’t understand your question.
Charles
Charles,
There is no “reply” link” at the end of your last answer of our previous exchange. From reading your bio, I understand that you are currently located in Italy. Thus what seems to be your unfamiliarity with Canadian Lotteries like Lotto-Max: 8 balls are drawn from the same device; the first 7s are the core combination of the draw, the 8th is a “bonus” ball. – You will find the details at this site: ” lotterycanada.com/ lotto-max ” .
My core question is about the # success in the binomial formula:
P(>=1) = 1-BINOM.DIST( s ; trials; p(s); true): For the # success: do I use “0” or “1” ?
Thank you and regards.
Pierre,
I now understand how the lottery works, but I still don’t understand what probability you are trying to calculate. Do you want to know the probability that you will win the lottery with 8 balls matching?
Charles
For each 49 ball of a next draw, considering the “history” of each balls:
With balls of similar “forecasted” values of P(>=1), I compose 8 balls combinations, that may win “something (?)”.
Voila !
Pierre,
Sorry, but I still don’t understand the underlying problem that you are looking to solve. When you speak about the “history” of a ball, I think that you want to factor in any defects in the ball which makes it come up more or less often (otherwise the history should be irrelevant). I don’t know what P(>=1) is referring to.
Charles
The probability for a # to be in a 8 ball combination in the next 10 draws of the this lottery
P(s:>=1) = 1-Binom.dist(s; 10; p(x); true).
I have tried both values for “s”; 0 and 1, with interesting outcomes that answers my questions.
Thank you for your time on my question. Your insights on this site are interesting and useful.
Regards.
Studying the historic draws of a lottery (Canada Lotto-Max), to assess the probability of “at least” 1 presence of a ball in n draws after its last known presence and “a” absences at the time of a d’th draw: this ball having a individual probability of P, may I use : 1-BINOM.DIST(0; n; P; True) ?
Or, I-NEGBINOM.DIST( “a”, 0, P, True) ?
Please advise. Thank you
Pierre,
Sorry, but I don’t completely understand the situation you are describing. Please describe the problem more clearly.
Charles
As of the last draw of Lotto-Max: a ball (x) has “n” presences, “a” absences; and a average probability of “p(x)”.
For exactly 1 presence in the next draw:
P(x) =NEGBINOM.DIST( “a”; 1 ; “p(x)”; false).
For at least 1 and more presence(s) in the next “d” draws: is it:
P(>=1) = 1-BINOM.DIST(0; d; P(x); true ) ? Where “0” = the “x-1” of a previous answer. . Thank you. Regards.
Pierre,
I don’t understand what “n” presences and “a” absences means. Is there one ball or many balls? I still don’t understand what the situation is.
Charles
Lotto-Max is a 7/49+1 lottery and all 8 balls are drawn from the same device.
As of a specific draw: a ball (x) has 47 presences; 4 absences since last drawn, and an average probability of p(x):
For the next 1st draw afterward:
P(x)=NEGBINOM.DIST(4; 1; p(x); false)
For the next d draws afterward:
P(>=1)=1-BINIOM.DIST(0 success; d trials; P(x); true) ?
Question is on: # success: 0 or 1 ?
I can’t figure out how to set up the BINOMDIST formula in Excel for P(>=X) [meaning greater than or equal to x]. I’ve worked on this problem for over 3 hours without success on this part. I already have working formulas for the remainder of the probabilities. Any help setting up the formula would be greatly appreciated.
Vicki,
Let’s do a specific example where the probability of success on each trial is .4 and there are 10 trials. The probability of getting 7 or fewer successes in the 10 trials is given by the formula =BINOMDIST(7,10,.4,TRUE). The probability of getting more than 7 successes in the 10 trials is therefore given by the formula =1-BINOMDIST(7,10,.4,TRUE). The probability of 8 or more successes is the same, namely =1-BINOMDIST(7,10,.4,TRUE).
In general, with n trials and the probability p of success on any one trial, the probability of x or more successes, what you called P(>=x), is given by the formula =1-BINOMDIST(x-1,n,p,TRUE).
Charles
CAN YOU PLEASE SHARE WITH ME THE REAL LIFE EXAMPLES WHERE BINOMIAL DISTRIBUTION WEN CANNOT APPLY?
IRFAN MALIK PAKISTAN
Irfan,
There are lots of examples throughout the website where the binomial distribution doesn’t apply. E.g. the binomial distribution is symmetric, and so for data which is very skewed the binomial distribution is not a good fit.
Charles
If the question is termed “What is the probability of at least 171 passengers showing up if the airline sold 184 tickets and the probability of passengers showing up is .93?”
I understand how to do it for a specific value, but how do I plug into excel for a question asking for “at least” a certain number of successes?
Clark,
BINOMDIST(171,184,.93,FALSE) = probability of that exactly 171 passengers show up
BINOMDIST(171,184,.93,TRUE) = probability of that at most 171 passengers show up
1-BINOMDIST(171,184,.93,TRUE) = probability of that more than 171 passengers show up = probability that at least 172 passengers show up
1-BINOMDIST(170,184,.93,TRUE) = probability that at least 171 passengers show up
Charles
Thanks Charles, That is what exactly I was looking for.
I am faced with the question, “Given three graphs with the same probability, what happens to the three graphs’ shapes as “n” increases?”
Annie,
Sorry, but I don’t understand what you mean by “Given three graphs with the same probability”. In any case, you can draw the three graphs as described on the website using Excel charting capabilities and see what happens.
Charles
Simple but at the same time very insightful.
Thanks for taking Your time to share the knowledge
i have a mean value of 30 participant, and standard deviation and other measure,i want to plot probability distribution function. is it possible?
Jai,
It depends on the distribution. As you can see from the formulas for the probability density function for the normal distribution if you have data for the mean and standard deviation you can plot the distribution. For the binomial distribution you need n and p (as shown in Figure 1 of the referenced page). But since mean = np and std dev = the square root of np(1-p) (by Property 1), you can solve for n and p and then plot the distribution. If I’ve done the algebra correctly, if m = the mean and s = the std dev, then p = 1-s^2/m and n = m^2/(m-s^2).
Charles