Preliminary Property
Property A: If z has distribution N(0, 1), u2 has distribution χ2(m) and z and u are independent, then
has distribution T(m).
Proof: Since z has distribution N(0, 1), any linear combination of z is also normal, and in particular y = z has distribution N(0,
). Let f the pdf for y. Therefore
Let x = u2. Thus u = , and so using the change of variables technique (Theorem 2 of General Properties of Distributions), if the pdf of x is h, then the pdf g of u is
But since x = u2 has distribution χ2(m), we have
Since t = y/u is an increasing function of y, keeping u fixed, if k(u, y) is the joint frequency function of u and y, and h(u, t) is the joint frequency function of u and t, then by a corollary to the change of variables technique,
Since y and u are independently distributed and y = tu,
It now follows that the pdf q(t) of t is given by
which completes the proof.
Principal Theorem
Theorem 1: If x has normal distribution N(μ, σ2), then for samples of size n, the random variable
has distribution T(n – 1).
Proof: Since x has normal distribution, by the Central Limit Theorem the sample mean has normal distribution , and so z has distribution N(0, 1) where
By Corollary 3 of Chi-square Distribution, for samples of size n the sample variance s2 has distribution
Now define the random variable u2 as follows:
It now follows that u2 has distribution χ2(n–1). Finally define the random variable t as follows
From Property A, since it can be shown that x̄ and s2 are independently distributed, it follows that t has distribution T(n–1). But also,
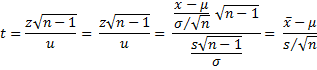 References
References
Soch, J. (2021) Proof: Relationship between normal distribution and t-distribution
https://statproofbook.github.io/P/norm-t
Wikipedia (2013) Student’s t-distribution
https://en.wikipedia.org/wiki/Student%27s_t-distribution#Characterization
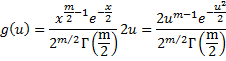
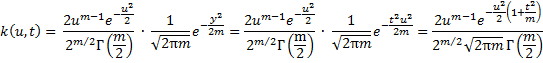
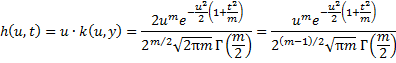
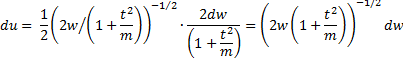
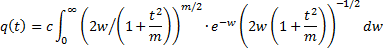
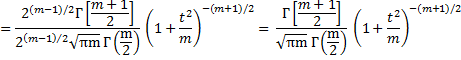
hi,
you typed
“Now define the random variable as follows:
u=(s*sqrt(n-1)/sigma)^2 ”
but when you inserting it into t it was sqrt(u)
i think that you have to define u as
u=(s*sqrt(n-1)/sigma)
Ghadeer,
Yes, there is a typing error. The equation with u should really be u^2. I have now corrected the webpage.
Thanks for identifying this error. I appreciate your help in making the website more accurate and easier to follow.
Charles
Ghadeer,
Yes, there is a typing error. The equation with u should really be u^2. I have now corrected the webpage.
Thanks for identifying this error. I appreciate your help in making the website more accurate and easier to follow.
Charles
Charles, I believe you have an error above, “Let x = u^2. Thus u = z * sqrt{x}, and so using the change of variables…”
If x=u^2 then that means u = sqrt(x), not z * sqrt(x).
regards,
Cristian
Cristian,
Thanks for catching this typo. I have just corrected the webpage per your suggestion. I appreciate your help in making the website better.
Charles