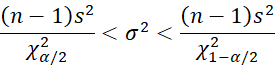For a few distributions, there are formulas for the standard error and confidence interval for the distribution parameters. For the others, we need to use iterative approaches as described elsewhere.
Normal distribution
For the normal distribution, we have seen in One-Sample Hypothesis Testing, the standard error of the mean can be estimated by se = s/√n where s is the sample standard deviation and n is the sample size. Thus, the 1 – α confidence interval for the mean is x̄ ± se · zcrit where zcrit = NORM.S.INV(1–α/2).
A better estimate is achieved by replacing zcrit by tcrit = T.INV.2T(α, n–1) as explained in One-Sample t-Test.
As described in One-Sample Testing of the Variance, the confidence interval for the variance σ2 is
where χα2 = CHISQ.INV.RT(α,n–1).
Exponential distribution
For relatively large samples (at least 15 or 20 elements), an estimate for the confidence interval of the rate parameter of an exponential distribution is
where λ is the estimate of the rate parameter based on a sample of size n.
Other distributions
There are various techniques for obtaining approximate confidence intervals for the parameters of some distributions For large samples, based on the central limit theorem, distribution parameters are approximately normally distributed, and so once we estimate the standard error of parameter θ, the 1–α confidence interval is
θ ± se · zcrit
We won’t explore these approaches further, but instead, use bootstrapping.
Reference
Tibshirani, R. (2014) The bootstrap. Advanced methods for data analysis
https://www.stat.cmu.edu/~ryantibs/advmethods/notes/bootstrap.pdf