Single Sample Hypothesis Testing

Basic Concepts

Suppose we take a sample of size n from a normal population N(μ, σ²) and ask whether the sample mean differs significantly from the overall population mean.

This is equivalent to testing the following null hypothesis H₀: 

This is a two-tailed hypothesis, although sometimes a one-tailed hypothesis is preferable (see examples below). By Theorem 1 of Basic Concepts of Sampling Distributions, the sample mean has the normal distribution N(μ, σ²/n).

We can use this fact directly to test the null hypothesis or employ the following test statistic or employ the z-score as the test statistic; i.e.

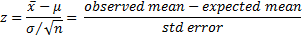Example

Example 1: National norms for a school mathematics proficiency exam are normally distributed with a mean of 80 and a standard deviation of 20. A random sample of 60 students from New York City is taken showing a mean proficiency score of 75. Do these sample scores differ significantly from the overall population mean based on a significance level of α = .05?

We would like to show that any deviation from the expected value of 80 for the sample mean is due to chance. We consider three approaches, each based on a different null hypothesis.

One-tailed Test (left-tail)

Suppose that before any data were collected we had postulated that a particular sample would have a mean lower than the presumed population mean (left-tailed null hypothesis H₀).

Note that we have stated the null hypothesis in a form that we want to reject; i.e. we are actually postulating the alternative hypothesis H₁

The distribution of the sample mean  is N(μ, σ²) where μ = 80, σ = 20 and n = 60. Since the standard error = = = 2.58, the distribution of the sample mean is N(80,2.58). The critical region is the left tail, representing α = 5% of the distribution. We now test to see whether x̄ is in the critical region.

critical value (left tail) = NORM.INV(α, μ, ) = NORM.INV(.05, 80, 2.58) = 75.75

Since we reject the null hypothesis.

Alternatively, we can test to see whether the p-value is less than α, namely

p-value = NORM.DIST(x̄, μ, ), TRUE) = NORM.DIST(75, 80, 2.58, TRUE) = .0264

Since p-value = .0264 < .05 = α, we again reject the null hypothesis.

Another approach for arriving at the same conclusion is to use the z-score

Based on either of the following tests, we again reject the null hypothesis:

p-value = NORM.S.DIST(z, TRUE) = NORM.S.DIST(-1.94, TRUE) = .0264 < .05 = α

z_crit = NORM.S.INV(α) = -1.64 > – 1.94 = z_obs

The conclusion from all these approaches is that the sample mean is significantly lower than the presumed population mean, and so the sample has significantly lower scores than what would be found in the general population.

One-tailed Test (right-tail)

Suppose that before any data were collected we had postulated that the sample mean would be higher than the presumed population mean (right-tailed hypothesis H₀).

This time, the critical region is the right tail, representing α = 5% of the distribution. We can now run any of the following four tests:

p-value = 1 – NORM.DIST(75, 80, 2.58, TRUE) = 1 – .0264 = .9736 > .05 = α

x̄_crit = NORM.INV(.95, 80, 2.58) = 84.25 > 75 = x̄_obs

p-value = 1 – NORM.S.DIST(-1.94, TRUE) = 1 – .0264 = .9736 > .05 = α

z_crit = NORM.S.INV(.95) = 1.64 > -1.94 = z_obs

We retain the null hypothesis and conclude that we do not have enough evidence to claim that the sample mean is higher than the presumed population mean.

Two-tailed Test

Suppose that before any data were collected we had postulated that a particular sample would have a mean different from the presumed population mean (two-tailed hypothesis H₀).

Here we are testing to see whether the sample mean is significantly higher or lower than the population mean (alternative hypothesis H₁).

This time, the critical region is a combination of the left tail representing α/2 = 2.5% of the distribution, plus the right tail representing α/2 = 2.5% of the distribution. Once again we test to see whether x̄ is in the critical region, in which case we reject the null hypothesis.

Due to the symmetry of the normal distribution, the p-value =

Thus, testing whether p-value < α is equivalent to testing whether

P(x̄ < 75) = NORM.DIST(75, 80, 2.58, TRUE) < α/2

Since

NORM.DIST(75, 80, 2.58, TRUE) = .0264 > .025 = α/2

we cannot reject the null hypothesis. We can reach the same conclusion as follows:

x̄_crit-left = NORM.INV(.025, 80, 2.58) = 74.94 < 75 = x̄_obs

If the sample mean had been x̄_obs = 85 instead of 75, then this test would become

x̄_crit-right = NORM.INV(.975, 80, 2.58) = 85.06 > 85 = x̄_obs

In either case, x̄_obs would lie just outside the critical region, and so we would retain the null hypothesis. Finally, we can reach the same conclusion by testing the z-score in either of the following ways:

NORM.S.DIST(-1.94, TRUE) = .0264 > .025 = α/2

|z_obs| = 1.94 < 1.96 = NORM.S.INV(.975) = |z_crit|

We could alternatively use either of the following tests:

p-value = 2*(1-NORM.S.DIST(-1.94, TRUE)) = .0528 > .05 = α

p-value = 2*NORM.S.DIST(|-1.94|, TRUE) = .0528 > .05 = α

Example with a larger sample

Example 2: Suppose that in the previous example, we took a larger sample of 100 students and once again the sample mean was 75. Repeat the two-tailed test.

This time the sample error =  = = 2, and so

NORM.DIST(75, 80, 2, TRUE) = .006 < .025 = α/2.

This time we reject the null hypothesis and conclude that there is a significant difference between the sample and population means. Note that this test is equivalent to

p-value = 2* NORM.DIST(75, 80, 2, TRUE) = .012 < .05 = α.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Howell, D. C. (2010) Statistical methods for psychology, 7th Ed. Wadsworth. Cengage Learning
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf