Objective
On this webpage, we explore the concepts of a confidence interval and prediction interval associated with simple linear regression, i.e. a linear regression with one independent variable x (and dependent variable y), based on sample data of the form (x1, y1), …, (xn, yn). We also show how to calculate these intervals in Excel. In Confidence and Prediction Intervals we extend these concepts to multiple linear regression, where there may be more than one independent variable.
Confidence Interval
The 95% confidence interval for the forecasted values ŷ of x is
Here, sy⋅x is the standard estimate of the error, as defined in Definition 3 of Regression Analysis, Sx is the squared deviation of the x-values in the sample (see Measures of Variability), and tcrit is the critical value of the t distribution for the specified significance level α divided by 2. How to calculate these values is described in Example 1, below.
The 95% confidence interval is commonly interpreted as there is a 95% probability that the true linear regression line of the population will lie within the confidence interval of the regression line calculated from the sample data. This is not quite accurate, as explained in Confidence Interval, but it will do for now.
Figure 1 – Confidence interval
In the graph on the left of Figure 1, a linear regression line is calculated to fit the sample data points. The confidence interval consists of the space between the two curves (dotted lines). Thus there is a 95% probability that the true best-fit line for the population lies within the confidence interval (e.g. any of the lines in the figure on the right above).
Prediction Interval
There is also a concept called a prediction interval. Here we look at any specific value of x, x0, and find an interval around the predicted value ŷ0 for x0 such that there is a 95% probability that the real value of y (in the population) corresponding to x0 is within this interval (see the graph on the right side of Figure 1). Again, this is not quite accurate, but it will do for now.
The 95% prediction interval of the forecasted value ŷ0 for x0 is
where the standard error of the prediction is
For any specific value x0 the prediction interval is more meaningful than the confidence interval.
Example
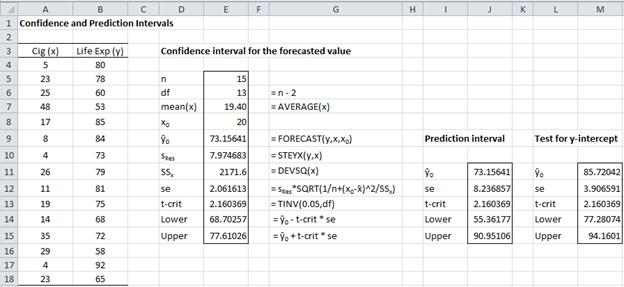
Example 1: Find the 95% confidence and prediction intervals for the forecasted life expectancy for men who smoke 20 cigarettes in Example 1 of Method of Least Squares.
Figure 2 – Confidence and prediction intervals
Referring to Figure 2, we see that the forecasted value for 20 cigarettes is given by FORECAST(20,B4:B18,A4:A18) = 73.16. The confidence interval, calculated using the standard error of 2.06 (found in cell E12), is (68.70, 77.61).
The prediction interval is calculated in a similar way using the prediction standard error of 8.24 (found in cell J12). Thus life expectancy of men who smoke 20 cigarettes is in the interval (55.36, 90.95) with 95% probability.
Graphical representation
You can create charts of the confidence interval or prediction interval for a regression model. This is demonstrated at Charts of Regression Intervals. You can also use the Real Statistics Confidence and Prediction Interval Plots data analysis tool to do this, as described on that webpage.
Testing the y-intercept
Example 2: Test whether the y-intercept is 0.
We use the same approach as that used in Example 1 to find the confidence interval of ŷ when x = 0 (this is the y-intercept). The result is given in column M of Figure 2. Here the standard error is
and so the confidence interval is
Since 0 is not in this interval, the null hypothesis that the y-intercept is zero is rejected.
Reference
Howell, D. C. (2009) Statistical methods for psychology, 7th ed. Cengage.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf




Hi Charles! Great webpage. Just a quick comment / correction. Prediction intervals are wider than confidence intervals as they are predicting individual measurement values that might be taken as further samples from the wider population. Thus I think that in the Figure 1, prediction intervals are illustrated on the LEFT, whereas confidence intervals (of the regressed mean value) are illustrated on the RIGHT. Your description below the Prediction Interval heading is also a bit confusing about this point: I would clarify “such that there is a 95% probability that the real value of y (in the population) ” to “such that there is a 95% probability that any measured value of y (the spread of the population, not its mean)”.
Hi John,
Glad that you found the webpage helpful.
1. The left side of Figure 1 shows the observed points, the regression line and the confidence interval. The right side shows the same confidence interval and some alternative regression lines that fit within the confidence interval (if the experiment is repeated with new observations). Both pictures are for the confidence interval. Neither for the prediction interval.
2. I don’t quite understand your comment about the prediction interval.
Charles
Hi Charles,
Great site.
Have a query, which I hope you can help me with.
For a prediction interval for a fixed regression, I’ve seen a formula as follows:
+/- Tvalue* STDEV(Y values)*SQRT (1 + 1/n)
This provides a much wider range than the PI formula you use above for a Y-on-X.
Is this right? I think the PI should be reflecting the distribution of data, rather than be affected by a change in regression line used to fit the data (we have CI for this).
If it is correct, can you explain the rationale for a range being much wider? I’m struggling to find an explanation online and the PI range looks far too wide relative to the data points.
Hi Russ,
I am please that you like the the website.
Do you have a reference for this formula? Which Tvalue is used?
Charles
Hi Charles,
T value is as per your formulas (related to alpha and df).
A former colleague put this formula into a spreadsheet which I am revising/cleaning, so unfortunately I don’t have an audit trial for it.
If it’s not familiar to you – I suspect it’s an error!
Kind regards
Russ
Hi Russ,
The formula that you displayed contains the term SQRT (1 + 1/n). As described on this webpage, the correct term takes the form SQRT (1 + 1/n + q) where q is as described on the webpage.
Perhaps the q term was just omitted.
Charles
Dear Charles:
I have a doubt. In wear reliability analysis is common to use the operational time t as independent variable ‘x’ and the thickness of a component (a measure of wear) as a dependent variable ‘y’, because the causality in that direction is obvious. But if I need to use least squares simple regression model to predict the operational time (with a estimated confidence interval) at which that component gets a critical thickness:
(a) is valid to conserve ‘y’ (thickness of the component) as a dependent variable and ‘x’ (operational time t) as a independent variable?, or
(b) the correct way is to invert variables, making ‘x’ (operational time t) the dependent variable and ‘y’ (thickness of the component) the independent variable?
(c) Is the statement in (b) incorrect because it’s contrary to causality direction?
I will be waiting for your answer.
Thank you.
Hello William,
If I understand the scenario you are describing correctly, it seems to me that (b) is correct. I don’t think that the causality direction matters.
Charles
Thank you very much for your response, Charles.
Then, if I understood, applying (b), making ‘x’ (operational time t) the dependent variable and ‘y’ (thickness of the component) the independent variable, I can get the next linear model (contrary to the causality direction):
x= b0+b1*y
And I can estimate b0 and b1 by least squares method, and applying the theory for predictive intervals, I can obtain a predictive interval for operating time t, ‘x’, for a specific critical value of thickness, ‘y0’, with the next formulas:
x0=b0+b1*x0
x0 upper= x0+tcrit*se
x0 lower= x0-tcrit*s.e
(with s.e: standard error of the prediction).
Is that correct?
I will be waiting for your answer.
Regards.
William,
I think that what you have written is correct, but I don’t understand x0=b0+b1*x0.
Charles
Hello, Charles.
It was a typo.
The correct expression is:
x0=bo+b1*y0
Then:
x0 upper= x0+tcrit*se
x0 lower= x0-tcrit*s.e
(with s.e: standard error of the prediction)
Thank you very much for your answer.
Regards.
I am very impressed with this site. The information is clear an useful. Dr. Zaiontz makes corrections when warranted, and says “I don’t know” when he doesn’t. Those are very nice behaviors, and too rare.
This site is helping me understand the different CIs which can be returned by Matlab’s predict() function.
Thank you, Dr. Zaiontz.
Thank you very much for your kind words, William.
Charles
Hello, and thank you for a very interesting article. Now I have a question.
I understand that the formula for the prediction confidence interval is constructed to give you the uncertainty of one new sample, if you determine that sample value from the calibrated data (that has been calibrated using n previous data points).
But suppose you measure several new samples (m), and calculate the average response from all those m samples, each determined from the same calibrated line with the n previous data points (as before). Shouldn’t the confidence interval be reduced as the number m increases, and if so, how? Can you divide the confidence interval with the square root of m (because this if how the standard error of an average value relates to number of samples)?
Best regards,
Hello Jonas,
I haven’t investigated this situation before. In Zar’s textbook, he handles similar situations. I suggest that you look at formula (20.40).
If this isn’t sufficient for your needs, usually bootstrapping is the way to go.
Charles
Thank you for that. Could you please explain what is meant by bootstrapping?
Hi Jonas,
Please see the following webpages:
https://real-statistics.com/resampling-procedures/
https://www.real-statistics.com/non-parametric-tests/bootstrapping/
Charles
unfortunately useless as tcrit is not defined in the text, nor it s equation given
Hello Vincent,
Yes, you are correct. Thank you for flagging this.
I have now revised the webpage, hopefully making things clearer.
Charles
The t-crit is incorrect, I guess. If alpha is 0.05 (95% CI), then t-crit should be with alpha/2, i.e., 0.025.
Right?
Hello Falak,
Yes, you are quite right. I have modified this part of the webpage as you have suggested.
Thank you very much for your help.
Charles
What if the data represents L number of samples, each tested at M values of X, to yield N=L*M data points. This would effectively create M number of “clouds” of data. Consider the primary interest is the prediction interval in Y capturing the next sample tested only at a specific X value. Should the degrees of freedom for tcrit still be based on N, or should it be based on L? And should the 1/N in the sqrt term be 1/M? Because it feels like using N=L*M for both is creating a prediction interval based on an assumption of independence of all the samples that is violated.
Hi Mike,
Sorry, but I don’t understand the scenario that you are describing. Have you created one regression model or several, each with its own intervals?
Charles
Only one regression: line fit of all the data combined. I’m just wondering about the 1/N in the sqrt term of the expanded prediction interval. Is it always the # of data points? My concern is when that number is significantly different than the number of test samples from which the data was collected. Say there are L number of samples and each one is tested at M number of the same X values to produce N data points (X,Y). Then N=LxM (total number of data points). In this case, the data points are not independent. So if I am interested in the prediction interval about Yo for a random sample at Xo, I would think the 1/N should be 1/M in the sqrt.
But since I am not modeling the sample as a categorical variable, I would assume tcrit is still based on DOF=N-2, and not M-2.
Sorry, Mike, but I don’t know how to address your comment.
Charles
When you test whether y-intercept=0, why did you calculate confidence interval instead of prediction interval?
Hi Ben,
This is a confusing topic, but in this case, I am not looking for the interval around the predicted value ŷ0 for x0 = 0 such that there is a 95% probability that the real value of y (in the population) corresponding to x0 is within this interval.
Charles
Hi Charles,
Hope you are well.
If i have two independent variables, how will we able to derive the prediction interval. looking forward to your reply.
thanks
See https://www.real-statistics.com/multiple-regression/confidence-and-prediction-intervals/
Charles
Hi Charles,
great page, very helpful.
tnks a lot.
Rafael Gamboa
Hi, I’m a little bit confused as to whether the term 1 in the equation in https://www.real-statistics.com/wp-content/uploads/2012/12/standard-error-prediction.png should really be there, under the root sign, because in your excel screenshot https://www.real-statistics.com/wp-content/uploads/2012/12/confidence-prediction-intervals-excel.jpg the term 1 is not there. I double-checked the calculations and obtain the same results using the presented formulae.
So from where does the term 1 under the root sign come? Just to make sure that it wasn’t omitted by mistake…
Hi Erik,
The 1 is included when calculating the prediction interval is calculated and the 1 is dropped when calculating the confidence interval.
Charles
Ah, now I see, thank you. I am a lousy reader…
That means the prediction interval is quite a lot worse than the confidence interval for the regression…
I’m quite confused with your statements like:
“This means that there is a 95% probability that the true linear regression line of the population will lie within the confidence interval of the regression line calculated from the sample data.”
One cannot say that! The correct statement should be that we are 95% confident that a particular CI captures the true regression line of the population.
If we repeatedly sampled the population, then the resulting confidence intervals of the prediction would contain the true regression, on average, 95% of the time.
Yes, you are correct. I have inadvertently made a classic mistake and will correct the statement shortly. Thanks for bringing this to my attention.
Charles
Actually they can. The ‘particular CI’ you speak of stud, is the ‘confidence interval of the regression line calculated from the sample data’. All estimates are from sample data. What you are saying is almost exactly what was in the article. You are probably used to talking about prediction intervals your way, but other equally correct ways exist. (and also many incorrect ways, but this isn’t the case here). Be open, be understanding.
Im confused with a question im stuck on:
in a regression analysis the width of a confidence interval for predicted y^, given a particular value of x0 will decrease if
a: n is decreased
b: X0 is moved closer to the mean of x
c: Confidence level is increased
d: Confidence level is decreased
I don’t completely understand the choices a through d, but the following are true:
The smaller the value of n, the larger the standard error and so the wider the prediction interval for any point where x = x0
The standard error of the prediction will be smaller the closer x0 is to the mean of the x values. In this case the prediction interval will be smaller
Charles
so which choices is correct as only one is from the multiple answers?
its a question with different answers and one if correct but im not sure which one.
Hassan,
My previous response gave you the information you need to pick the correct answer.
Charles
Hi Charles,
Why aren’t the confidence intervals in figure 1 linear (why are they curved)?
John,
That is the way the mathematics works out (more uncertainty the farther from the center). Why do you expect that the bands would be linear?
Charles
Your post makes it super easy to understand confidence and prediction intervals. The excel table makes it clear what is what and how to calculate them. Congratulations!!!
I put this website on my bookmarks for future reference.
Thank you!
Hi Charles
What’s the difference between the root mean square error and the standard error of the prediction? I’ve been taught that the prediction interval is 2 x RMSE. Thank you for the clarity.
Hi Sean,
The version that uses RMSE is described at
https://www.real-statistics.com/multiple-regression/confidence-and-prediction-intervals/
Note that the formula is a bit more complicated than 2 x RMSE. Note too the difference between the confidence interval and the prediction interval. Also, note that the 2 is really 1.96 rounded off to the nearest integer.
Charles
To proof homoscedasticity of a lineal regression model can I use a value of significance equal to 0.01 instead of 0.05?
Carlos,
What is your motivation for doing this?
Charles
I want to know if is statistically valid to use alpha=0.01, because with alpha=0.05 the p-value is smaller than 0.05, but with alpha=0.01 the p-value is greater than 0.05.
Carlos,
The setting for alpha is quite arbitrary, although it is usually set to .05. You shouldn’t shop around for an alpha value that you like. You can simply report the p-value and worry less about the alpha value.
Charles
Hi Charles, thanks again for your reply. For the mean, I can see that the t-distribution can describe the confidence interval on the mean as in your example, so that would be 50/95 (i.e. p = 0.5, confidence =95%). Then I can see that there is a prediction interval between the upper and lower prediction bounds i.e. say p = 0.95, in which 95% of all points should lie, what isn’t apparent is the confidence in this interval i.e. 95/??
I used Monte Carlo analysis (drawing samples of 15 at random from the Normal distribution) to calculate a statistic that would take the variable beyond the upper prediction level (of the underlying Normal distribution) of interest (p=.975 in my case) 90% of the time, i.e. 97.5/90. So it is understanding the confidence level in an upper bound prediction made with the t-distribution that is my dilemma.
Ian,
I have tried to understand your comments, but until now I haven’t been able to figure the approach you are using or what problem you are trying to overcome.
Charles
Hi Ian,
I believe the 95% prediction interval is the average. I think the 2.72 that you have derived by Monte Carlo analysis is the tolerance interval k factor, which can be found from tables, for the 97.5% upper bound with 90% confidence.
Hope this helps,
Mark.