Lin’s Concordance Correlation Coefficient

Objective

Like Bland-Altman or Deming Regression, Lin’s Concordance Correlation Coefficient (CCC) is a method for comparing two measurements of the same variable. This is especially important if you are trying to introduce a new measurement capability that has some advantages (e.g. it is less expensive or safer to use) over an existing measurement technique (the “gold standard”).

Definition and Interpretation

Lin’s CCC  between two random variables x and y is defined as

where ρ  is the correlation coefficient between variables x and y. Lin’s CCC is equivalent to 1 minus the ratio of the expected orthogonal squared distance from the line y = x and the expected orthogonal squared distance from the line y = x assuming independence.

The sample version of Lin’s CCC is

Here, we use the population versions of s_x and s_y, in that we divide by n instead of by n–1. The calculation is reasonably accurate for n ≥ 10.

Like a correlation coefficient, -1 ≤ ρ_C ≤ 1 and -1 ≤ r_C ≤ 1 .

Values near +1 indicate strong concordance between x and y, values near -1 indicate strong discordance, and values near zero indicate no concordance. There is no clear-cut agreement as to how to interpret other values, although one approach is to interpret Lin’s CCC as for Pearson’s correlation coefficient (e.g. values less than .20 are poor, while values greater than .80 are excellent).

McBride recommends much more stringent requirements (less than .90 is poor, .90-.95 moderate, .95-.99 substantial, and greater than .99 is excellent). 

Confidence Interval

To calculate a confidence interval, first, apply the Fisher transform to Lin’s CCC to get r′_C and then use the following standard error for the transformed value.

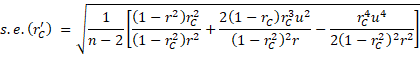where

The confidence interval for the transformed value of ρ_C is then

Taking the inverse Fisher transform yields the desired confidence interval for ρ_C.

Example

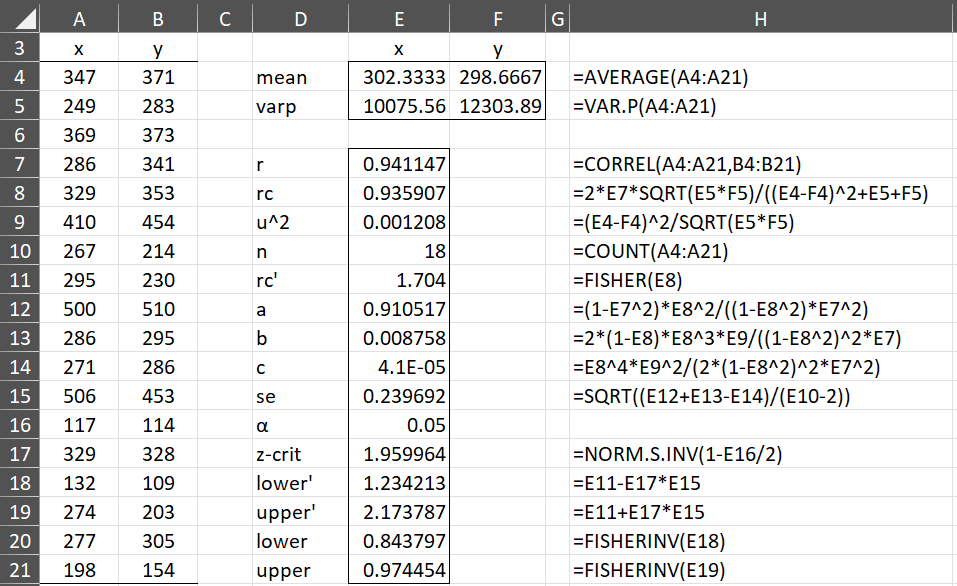
Example 1: Calculate Lin’s CCC for the data in range A3:B21 of Figure 1 as well as the 95% confidence interval.

The Excel calculations are shown in columns E and F of Figure 1 and column H shows the formulas in column E. Lin’s CCC is .9359 and the 95% confidence interval is (.8438, .9745).

Figure 1 – Lin’s Concordance Correlation Coefficient

We see from Figure 2 that the data (shown in blue) aligns pretty well along the diagonal line y = x (shown in red).

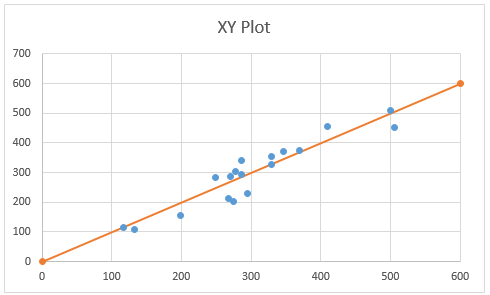
Figure 2 – Chart of the data

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack contains the following array function:

LINCCC(R1, R2, lab, alpha): returns a column array with the values Lin’s concordance correlation coefficient plus the lower and upper ends of the 1–alpha confidence interval; alpha is the significance level (default .05); if lab = TRUE then a column of labels is added to the output (default FALSE).

The formula =LINCCC(A4:A21,B4:B21,TRUE) produces the output for Example 1 as shown in Figure 3.

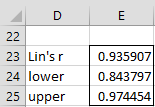
Figure 3 – Output from LINCCC

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Steichen, T. J. and Cox, N. J. (2002) A note on the concordance correlation coefficient. The Stata Journal.
https://journals.sagepub.com/doi/pdf/10.1177/1536867X0200200206

McBride, G. B. (2005) A proposal for strength-of-agreement criteria for Lin’s concordance correlation
https://www.medcalc.org/download/pdf/McBride2005.pdf