Factor Extraction

A number of methods are available to determine the factor loadings used for factor analysis. We will start by explaining the principal component method. Another commonly used method, the principal axis method, is presented in Principal Axis Method of Factor Extraction.

Using the concepts that are described in Basic Concepts of Factor Analysis, we show how to carry out factor analysis via the following example..

Example 1: Carry out the factor analysis for evaluating great teachers based on the data in Example 1 of Principal Component Analysis.

As we saw in Example 1 of Principal Component Analysis, nine criteria are measured. Our objective is to find a set of fewer than nine factors that reasonably captures what is a great teacher. In fact, we hope to find substantially fewer than nine factors that do the job.

Figure 1 shows the correlation matrix for this data (repeated from Figure 4 of Principal Component Analysis).

Correlation matrix teacher evaluations

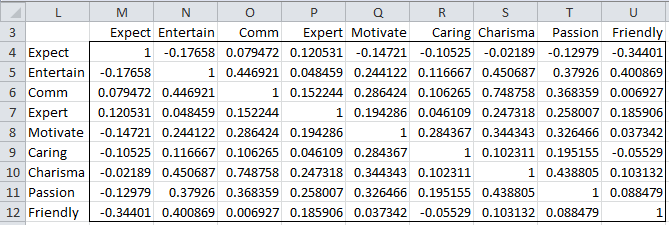
Figure 1 – Correlation Matrix

Figure 2 shows the table of eigenvalues and eigenvectors for the correlation matrix (repeated from in Figure 5 of Principal Component Analysis) using the Real Statistics function eigVECTSym(B6:J14).

Eigenvalues eigenvectors correlation matrix

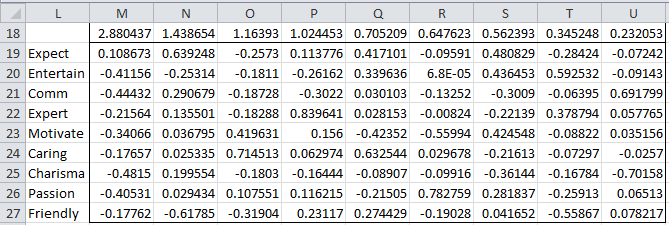
Figure 2 – Eigenvalues and eigenvectors

Using the formula bij = \sqrt \lambda_jcij where C1, …, Ck are the eigenvectors (range B19:J27 in Figure 2) corresponding to the eigenvalues (range B18:J18 in Figure 2) λ1 ≥ ⋯ ≥ λk, we calculate the loading factors for the nine common factors (see Figure 3).

Loading factors full model

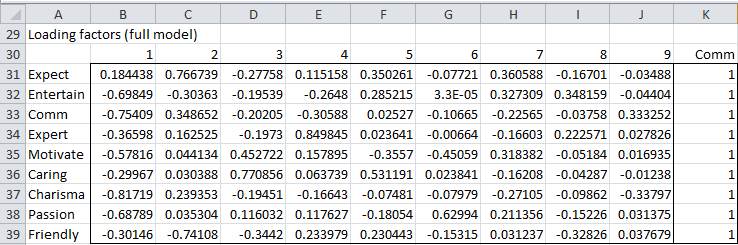
Figure 3 – Loading factors (full model)

For example, the loading factor of the Passion variable on Factor 1 (cell B38) is given by the formula =B26*SQRT(B$18). Figure 3 also contains the communalities (range K31:K39). The communality of each variable represents the portion of that variable’s variance captured by the model. For variable xi this is \sum_{j=1}^k b_{ij}^2. E.g., the communality of the Passion variable (cell K38) is calculated via the formula =SUMSQ(B38;J38). Since we are using the full model (where all nine common factors are present) and the variance of each variable is 1 (remember we standardized the data), it is not surprising that column K contains all ones.

15 thoughts on “Factor Extraction”

  1. Hi Charles,

    could you please explain me how could I obtain the factor correlations. It would be a square symmetric matrix of dimension mxm where m is the number of factors and diagonal 1.

    Thanks for your support

    Diego

    Reply

  2. Hello Charles,
    How can you get the X values, using: xi=mu + L.f + e ?
    Imagine you have 10 observations and 3 traits
    – x would be a 10×3 matrix
    – mu a 10 x 1 matrix

    But L.f’s shape wouldn’t match the shapes above?…how can we get back to the original x’s values once you have decomposed the X’s?

    I hope the question makes sense.

    I read somewhere you had a book ready to be published? 🙂

    Many thanks,
    Fred

    Reply

  3. Hi Charles,
    Regarding the first question, how to convert the original data value of X into a value of the factor Z. I understand from the tutorial, that x can be represented as a linear combination of Z but given X, how to know Z in order to proceed with the regression?
    Thanks.

    Reply

    • Lata,
      You use the factor loadings to convert your original data into data about the factors (i.e. the hidden variables). Then you perform regression on the data about the factor. This assumes that the y value is not part of your factor analysis.
      So if you had 100 samples about the vector X = (x1, …, x20) and then used factor analysis to find factors Z = (z1, z2, z3) you would perform regression using the data (z11, z21, z31, y1), …., (z1H, z2H, z3H, yH). Here H simply means 100.
      Charles

      Reply

    • Rohit,
      Calculation of the factor loadings is part of a process that identifies hidden factors and how to interpret the original variables in terms of the hidden factors.
      Charles

      Reply

Leave a Comment