Basic Concepts
Generally to understand some characteristic of the general population we take a random sample and study the corresponding property for the sample. We then determine whether any conclusions reached about the sample are representative of the population.
This is done by choosing an estimator function for the characteristic (of the population) that we want to study and then applying this function to the sample to obtain an estimate. By using the appropriate statistical test we then determine whether this estimate is based solely on chance.
The hypothesis that the estimate is based solely on chance is called the null hypothesis. Thus, the null hypothesis is valid if the observed data (in the sample) do not differ from what would be expected based on chance alone. The complement of the null hypothesis is called the alternative hypothesis.
The null hypothesis is typically abbreviated as H0 and the alternative hypothesis as H1. Since the two are complementary (i.e. H0 is true if and only if H1 is false), it is sufficient to define the null hypothesis.
Caution
Since the sample usually only contains a subset of the data in the population, we cannot be certain as to whether the null hypothesis is true or not. We can merely gather information (via statistical tests) to determine whether it is likely or not. We therefore speak about rejecting or not rejecting (aka retaining) the null hypothesis based on some test, but not accepting the null hypothesis or the alternative hypothesis. Often in an experiment, we are actually determining the validity of the alternative hypothesis by testing whether or not to reject the null hypothesis.
Types of Error
When performing such tests, there is some chance that we will reach the wrong conclusion. In fact, here are two types of such errors:
- Type I – H0 is rejected even though it is true (false positive)
- Type II – H0 is not rejected even though it is false (false negative)
The acceptable level of Type I error is designated by alpha (α), while the acceptable level of Type II error is designated beta (β).
Significance
We use the following terminology:
Significance level is the acceptable level of type I error, denoted α. Typically, a significance level of α = .05 is used (although sometimes other levels such as α = .01 may be employed). In other words, we are willing to accept the fact that in 1 out of every 20 samples we reject the null hypothesis even though it is valid.
P-value (the probability value) is the value p of the statistic used to test the null hypothesis. If p < α then we reject the null hypothesis.
Critical region is the part of the sample space that corresponds to the rejection of the null hypothesis, i.e. the set of possible values of the test statistic that are better explained by the alternative hypothesis. The significance level is the probability that the test statistic will fall within the critical region when the null hypothesis is assumed to be true.
Usually, the critical region is depicted as a region under a curve for continuous distributions (or a portion of a bar chart for discrete distributions).
The typical approach for testing a null hypothesis is to select a statistic based on a sample of fixed size, calculate the value of the statistic for the sample, and then reject the null hypothesis if and only if the statistic falls in the critical region.
One-tailed tests
One-tailed hypothesis testing specifies the direction of the statistical test. For example, to test whether cloud seeding increases the average annual rainfall in an area that usually has an average annual rainfall of 20 cm, we define the null and alternative hypotheses as follows, where μ represents the average rainfall after cloud seeding.
H0: µ ≤ 20 (i.e. average rainfall does not increase after cloud seeding)
H1: µ > 20 (i.e. average rainfall increases after cloud seeding
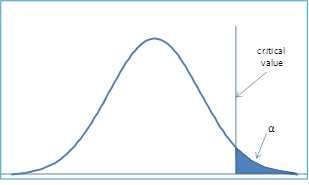
Here the experimenters are quite sure that the cloud seeding will not significantly reduce rainfall, and so a one-tailed test is used where the critical region is the shaded area in Figure 1. The null hypothesis is rejected only if the test statistic falls in the critical region, i.e. the test statistic has a value greater than the critical value.
Figure 1 – Critical region is the right tail
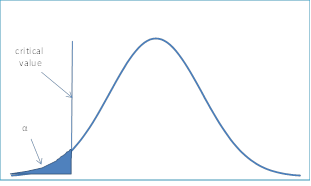
The critical value region here is the right (or upper) tail. It is quite possible to have one-sided tests where the critical region is the left (or lower) tail. For example, suppose the cloud seeding is expected to decrease rainfall. Then the null hypothesis would be as follows:
H0: µ ≥ 20 (i.e. average rainfall does not decrease after cloud seeding)
H1: µ < 20 (i.e. average rain decreases after cloud seeding)
Figure 2 – Critical region is the left tail
Two-tailed tests
Two-tailed hypothesis testing doesn’t specify the direction of the test. For the cloud seeding example, it is more common to use a two-tailed test. Here the null and alternative hypotheses are as follows.
H0: µ = 20
H1: µ ≠ 20
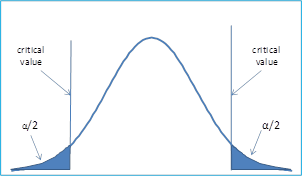
The reason for using a two-tailed test is that even though the experimenters expect cloud seeding to increase rainfall, it is possible that the reverse occurs and, in fact, a significant decrease in rainfall results. To take care of this possibility, a two-tailed test is used with the critical region consisting of both the upper and lower tails.
Figure 3 – Two-tailed hypothesis testing
In this case, we reject the null hypothesis if the test statistic falls on either side of the critical region. To achieve a significance level of α, the critical region in each tail must have size α/2.
Statistical power
Statistical power is 1 – β. Thus power is the probability that you find an effect when one exists, i.e. the probability of correctly rejecting a false null hypothesis. While a significance level for type I error of α = .05 is typically used, generally the target for β is .20 or .10, and so .80 or .90 is used as the target value for power.
Testing procedure
The general procedure for testing the null hypothesis is as follows:
- State the null and alternative hypotheses
- Specify α and the sample size
- Select an appropriate statistical test
- Collect data (note that the previous steps should be done before collecting data)
- Compute the test statistic based on the sample data
- Determine the p-value associated with the statistic
- Decide whether to reject the null hypothesis by comparing the p-value to α (i.e. reject the null hypothesis if p < α)
- Report your results, including effect sizes and confidence intervals
Caution
Suppose you perform a statistical test of the null hypothesis with α = .05 and obtain a p-value of p = .04, thereby rejecting the null hypothesis. This does not mean there is a 4% probability of the null hypothesis being true, i.e. P(H0) =.04. What you have shown instead is that assuming the null hypothesis is true, the conditional probability that the sample data exhibits the obtained test statistic is 0.04; i.e. P(D|H0) =.04 where D = the event that the sample data exhibits the observed test statistic.
References
Howell, D. C. (2010) Statistical methods for psychology, 7th Ed. Wadsworth. Cengage Learning
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
Zar. J. H. (2010) Biostatistical analysis 5th Ed. Pearson
3. A social worker wants to test (at = 0.05) whether the average body mass index (BMI) of the pupils under the feeding program is different from 18.2 kg. [
a) State the null and alternative hypothesis in words.
b) State the null and alternative hypothesis in symbols.
c) What is the probability of committing Type I error?
d) State the conclusion when H0 is rejected.
e) State the conclusion when H0 is not rejected.
Mikay,
This sounds like a homework problem. I have a policy of not doing students’ homework.
If you try to answer the questions, I can try to help you.
Charles
Hi Charles,
I have been having trouble over determining the null and alternative hypothesis for this question and was wondering if you could double check if they are correct.
The marriage premium has the greatest impact on younger players and weak-to-no impact on older players.
For younger players I have put:
𝐻_0= µ1 – µ2=0 (no difference between means of married and unmarried players)
𝐻_𝑎= µ1-µ2>0
and older players:
𝐻_0= µ1 – µ2≥0
𝐻_𝑎= µ1-µ2<0
Thank you for the help
Cassandra,
The wording is a little ambiguous. Your interpretation may be correct, but an alternative interpretation may be as follows:
If µ1 = the impact of the marriage premium on younger players and µ2 = the impact of the marriage premium on older players
𝐻_0= µ1<=µ2 𝐻_𝑎= µ1>µ2
Charles
Is the machine mixing the nuts at the ratio of 4:3:2:1?
what is the null and alternative hypothesis?
Sorry, but I don’t know what the ratio 4:3:2:1 means.
Charles
3. A researcher wants to compare the average intelligence of his students to the general population. He uses a standard IQ test, which has a population mean (µ) of 100 and a standard deviation (σ) of 16. The 50 students in his study scores an average of 105 on the IQ test. Test to see if the population mean is something different than 100 based on the sample data. Use an α = 0.05 for this test.
What is your question?
This looks to be a homework assignment. I have a policy of not doing homework assignments.
Charles
1. Two rival manufacturers of penlight batteries claimed that their product lasts longer than the other. Thirty samples of Brand A and thirty-four of Brand B were tested. The following are the lengths of lives of such batteries recorded in hours. Use .
Brand A
38 41 42 36 39 41 43 35 36 38 42 39 40 43 44
35 40 39 37 40 42 44 38 37 41 40 38 42 45 41
Brand B
38 40 41 43 39 41 40 43 39 38 40 43 44 39 40 41 42
39 40 45 40 38 42 41 40 36 37 41 42 40 36 38 41 40
solution:
H0:
Ha:
Level of significance:
Type of test and critical region/ p value:
Computations/ excel output:
Decision:
Conclusion:
What is your question? What do you think the null and alternative hypotheses are?
Charles
hello
I wanted to perform a t test, to check the hypothesis that activity of cell line1(sample1) is reduced to 50% compared to cell line2(sample 2).
these are independent events, so I tried doing a two sample t test assumed with different variance in excel sheet.
but I am not sure on how to put the null hypothesis for 50% reduction as difference in mean of samples. am I doing it correctly overall, what is your suggestion.
Harish,
One approach is to double the values in sample 1 and use the t test.
Charles
hello, can i ask for the null and alternative hypotheses of this problem ” In 2015, the monthly salary of doctors was compared based on gender. the number of doctors used as the research sample was 20. is there a significant difference in the earnings of doctors based on gender? ” And what statistical procedure i should use? thank you
The question “is there a significant difference in the earnings of doctors based on gender” should tell you what the null and alternative hypotheses are.
Charles
Hello. Can someone please help with the following question:The Department of Transportation in South Africa conducted a study a number of years ago that
showed that the proportion of cars tested which failed to meet the state pollution standard was
37%. The department would like to be able to say that the cars have improved since then. In a
sample of 100 cars more recently, the proportion not meeting the standards was 28%.
Are the cars better at meeting the standards than they used to be? Clearly state the null and
alternative hypotheses. Perform the hypothesis test at 99% confidence level and explain the
meaning of your conclusion.
(It’s 10 marks)
Michelle,
I suggest that you look at the one-sample proportion test. See
https://real-statistics.com/binomial-and-related-distributions/proportion-distribution/one-sample-proportion-testing/
Charles
I am struggling to understand how to write up my symbols for null and alternative hypothesis. This is the Case study given:
A video called “The Silent Scream” was produced as a gender violence prevention tool. A researcher tested whether the video influenced the attitude of viewers on gender based violence. Twenty volunteers completed a scale that measured their attitude and knowledge of gender violence. They then viewed the video. After the viewing they again completed the attitude and knowledge questionnaire. The before and after results on the questionnaire are provided below. A high score on this scale indicates a strong anti-violence against women sentiment.
N Pre-test Post-test score score
1 74 85
2 68 84
3 41 42
4 54 56
5 50 66
6 90 99
7 79 102
8 98 98
9 37 34
10 44 37
11 44 45
12 24 35
13 53 58
14 38 46
15 41 63
16 52 61
17 86 86
18 48 39
19 48 73
20 56 67
It was required of me to make use of Jamovi in order to answer questions using the 7-step decision.
Step 1: State the hypothesis
Null Hypothesis: “The Silent Scream” video has no effect on viewers attitude and knowledge towards gender violence.
Alternative Hypothesis: “The Silent Scream” video has an effect on viewers attitude and knowledge towards gender violence.
Is this correct and symbols should I use because there was a statistical significant difference .
The null and alternative hypotheses seem to be corrected stated.
Regarding the symbols to use, this depends on the test that you used to show that there is a statistically significant difference.
Here are the guidelines from the APA for how to state the results (at least in the psychology field).
https://blog.apastyle.org/apastyle/statistics/
Charles
Used a dependent t-test
Bella,
The APA guidelines describe how to report the results for this test.
Charles
Hello! Can someone help me to answer this? I badly needed. So this is the statement.
You have decided to undertake a project and have defined the main research question as “what are the opinions of consumers to a ten percent reduction in weight, with the orice remaining the same, of” Snackers” chocolate bar? ” Write a hypothesis that you could test in your project.
Thank you!
Hello Mary,
You could start by thinking about the types of opinions that consumers could have about this change.
You can think about how consumers might react to such a change. E.g. would this lower their opinion abou the product? would they buy less product?
Charles
Can you please try and solve this .the department conducted a study a number of years ago that showed that the proportion of cars tested which failed to meet the state pollution standard was 37%. The department would like to be able to say that the cars have improved since then. In a sample of 100 cars more recently,the proportion not meeting the standard was 28%.are the cars better at meeting the standards than they used to be ? Clealy state the null and alternative hypothesis.perfom on a 99% level of confidence
I suggest that you look at the Proportion Test portion of the Real Statistics website. See
https://real-statistics.com/binomial-and-related-distributions/proportion-distribution/
Charles
How would I go about this? Is this a Chi test as well?
A computer manufacturer is introducing a new product
specifically targeted at the home market and wishes to
compare the effectiveness of three distribution strategies:
computer stores, home electronics stores, and department
stores. Numbers of sales by 15 salespeople are recorded
here:
Electronics store: 5, 4, 3, 3, 3
Department store: 9, 7, 8, 6, 5
Computer store: 7, 4, 8, 4, 3
a Test the hypothesis that there is no difference between
the means of the retailers (α = .05).
b Select a multiple comparison test, if necessary, to determine
which groups differ in mean sales (α = .05).
This looks like a fit for one-way ANOVA. See
One-way ANOVA
Charles
Can I get some help with this? I am so lost. I am just learning about null and alternative hypothesis but this is part of my homework and I don’t even know where to begin
A random sample of students is interviewed to determine if there is an association between class and attitude toward corporations. With the following results, test the hypothesis that there is no difference among students on this attitude.
Favorable Neutral Unfavorable
Freshmen 100 50 70
Sophomores 80 60 70
Juniors 50 50 80
Seniors 40 60 90
See Independence Testing
Charles
Can I use Excel to do the calculations? If so, how?
Yes. How to do the calculations is explained on the suggested webpage.
Charles
kindly explain I will reject the null hypothesis or accept.
The confidence interval was 91% and the p-value was 0.09. How would you rephrase the hypothesis to publish the result?
Rephrase:
Hello Elena,
I assume that when you say that the “confidence interval was 91%” you mean that the significance level is alpha = .09. If the p-value is exactly equal to .09, then you are at the boundary between rejecting or not rejecting the null hypothesis. I have always assumed that p < alpha means that you reject the null hypothesis and so when p = alpha then you wouldn't reject the null hypothesis. This is quite arbitrary and others might disagree with this choice. Charles
Thank you very much for your response.
You can use a one-sample proportion test.
Charles
Hi, am i right or not ?
(a) A study to compare the effect of multiple intelligences approach and conventional approach on students’ mean score of Mathematics posttest among Form Two students after the effect of students’ mean score of Mathematics pre-test is controlled.
H0 : There is no significant difference on students’ mean score of Mathematics post-test among control group and experimental group of Form Two students after the effect of students’ mean score of Mathematics pre-test is controlled.
Ha : Students’ mean score of Mathematics post-test will higher than pre-test
(b) A study to determine whether self-concept and test anxiety contribute to primary school students’ motivation in learning.
H0 :Self-concept and test anxiety not a significant predictor to primary school students’ motivation in learning.
Ha : Self-concept and test anxiety contribute to primary school students’ motivation in learning.
(c) A study to compare the interpersonal skill between urban and rural primary school students.
H0 :There is no significant difference between urban and rural primary school students in interpersonal skill.
Ha : Urban primary school students’ interpersonal skill better than rural primary school students.
They all seem to be correct. All three use a one-tailed test.
Charles
Charles,
I would like to better understand the relationship between alpha and beta. For example if alpha is set at 0.05, and treatment data have an alternative distribution that makes beta = 0.20, could we say there is a 95% probability (1-alpha) there is an effect even though none exists, and a 80 % probability (1-beta) that there is an effect? It seems like these statements are contradictory. Can we reconcile them by saying there is a 15 % probability (beta-alpha) there is insufficient data to judge the effect?
Hi Dave,
Setting alpha = .05 means that we are willing to accept that in 1 out of every 20 samples we reject the null hypothesis even though it is true.
Setting beta =.20 means that we are willing to accept that 5 out of every 20 samples we accept the null hypothesis even though it is false.
These are not contradictory statements and your assertion about 15% probability is not correct.
Charles
Hi Charles,
Thanks for the clarification. I suppose another way to look at alpha and beta is that if I only want to minimize the chance of being wrong I should choose the hypothesis with the lower chance of being wrong, i.e. the alternative hypothesis if alpha (0.05) is less than beta (0.20).
Also, I’m sure you meant that “Setting beta=.20 means that we are willing to accept 4 out of every 20 samples…”
Hi Dave,
Generally alpha is less than beta, but this is not an appropriate way to decide.
Yes, you are correct: 4 out of 20.
Charles
Which of the following is the researcher usually interested in supporting when he or she is engaging in hypothesis testing?
a. The working hypothesis
b. The null hypothesis
c. Both the working and null hypothesis
d. Neither the working or null hypothesis
By definition, a.
Charles
Hello Charles,
I have a situation and I’m unsure of how to formulate any hypothesis and what method to use to analze it.
A medical drug is given to sample group(say, 100 patients) to decrease their values of, say, blood pressure (BP). We know their BP values before taking the drug and their BP values 1 month after taking the drug. (Data: mean BP before and after drug are X1 and X2, and the respective std. dev. are S1 and S2. Also since the BP reduces, X2<X1).
I want to show that BP reduces by at least 50% due to the drug. (The value of mean does reduce by more than 50% in sample).
Please tell me how to proceed.
Thanks.
Let x be the BP before treatment and y be twice the BP after treatment. The null hypothesis is
H0: mean-x >= mean-y.
You can use the t test to do the analysis provided the assumptions are met.
Note that I doubled the BP post-therapy to be able to test the 50% reduction. Obviously, you could have halved the pre-treatment BP values instead.
Charles
Hello Charles,
Thanks for the reply.
My samples are not independent so I cannot use the “Two samples t-test”. Instead I am using the Paired sample t-test.
Initial mean x1, final mean x2
Ho: x1-x2=50
s.e.=(std dev)/sqrt(n)
t=(K-50)/s.e.
then check p-value for this “t”.
Is the second approach, where I worked with percentages, acceptable ?
Second approach is similar to example on paired sample test on this website.
K= mean of percentage change in the values.
Ho: K>50
t=(K-50)/s.e.
I think I might have accidentally deleted some text as I was about to post a reply.
See the response to the other comment you sent me today.
Charles
Hello,
In your approach I don’t know what x1 and x2 are since you don’t have percentage values but BP values.
Using the approach from my previous comment, you can define x1 to be the BP before treatment and x2 to be twice the BP after treatment. The null hypothesis is then H0: meanx1 – meanx2 >= 0
You would use the paired t test
Charles
Thank you for your help, Charles.
In Mar 2018, Cold Storage started getting complaints from their Clients that they have been getting complaints from end consumers of the dairy products going sour and often smelling. On getting these complaints, the supervisor pulls out data of last 35 days temperatures. As a safety measure, the Supervisor has been vigilant to maintain the temperature below 3.9 deg C.
Assume 3.9 deg C as upper acceptable temperature range
What could be the null hypothesis and alternative hypothesis
Hello,
The question itself gives a pretty big clue as to what the null hypothesis and alternative hypothesis are. What is your best guess_
Charles
Hello Charles,
There are people who don’t know and are learning to understand what is null hypothesis and alternative hypothesis. It will be helpful to respond to the question to help not only the person who ask question but others who can understand by your response. Like for me, I am doing research to understand these words until I found your Web page but your answers did not help me to understand these words.
Hello Josianne,
Sorry about that, but I don’t recall ever getting a question from you.
I will answer the other comment that you sent me today.
Charles
Thanks Charles for reply. so can alternative hypothesis can have equal to sign? Ha:t>=3.9?
Hi Robin,
Generally, it is the null hypothesis that has the equal sign, but keep in mind that this is a minor detail. If you have reason to believe that t can’t be 3.9 then I guess it would be correct to put the equal sign with the alternative hypothesis. The testing would be identical.
Charles
Ho 3.9 .Is this correct
Hi Robin,
Sorry, but I don’t know what you are referring to.
Charles
Charles,Sorry mybad..I was referring to
H0>3.9
Ha<3.9
if i can reject null hypothesis saying temperature is greater than 3.9 then my alternative will be true that temp remains within or equal to 3.9
Hi Robin,
Yes, this is correct, although a better representation is:
H0: t > 3.9
Ha: t <= 3.9 Charles
hi i dnot understand the null hypothesis and alternative of this quory could you please help me?
h03.9 . is this correct?
Hello Meghan,
If you are referring to the comment you made to another webpage, then the null hypothesis should take the form:
H0: t >= 3.9 (here t = temperature). You goal is to give evidence that the null hypothesis is not correct (and so t < 3.9) Note that the clients might say that one incidence of t > 3.9 is already bad, in which case you don’t need to do statistical analysis and merely look at the data to see whether at least one of the elements is bigger than 3.9.
Charles
thanks charles
Hi Charles,
I have a dataset of water quality taken from different locations (130 locations). The data of some locations were significantly higher than the others. The standard value is 2000 mg/L. Request you to please help in finding the p-value for the dataset.
It will be a great help.
Dear Ruchi,
It depends on your null hypothesis and the statistical test that you use. What null hypothesis do you want to test?
Charles
Hi I’ve got an understanding about conducting hyposthesis but I needed a help in report that I’m writing as an assignment.
The sample I’ve taken is of 70 people and I have constructed two Hpothesis
1.There is no significant difference between employees of the private
sector and the public sector with regard to their pattern of savings that
lead to tax planning.
2. There is no significant difference between employees of the private
sector and the public sector with regard to their pattern of investments
in financial assets
3.There is no significant difference between employees of the private
sector and the public sector with regard to their level of awareness on
taxation laws and tax planning measures under the Income Tax Act
What am I supposed to do next
You need to decide on the type of design that you will use to test your hypothesis. Then you need to create a sample (or samples), as apparently you have done. You then need to determine which type of statistical test to use to test your hypothesis. For the type of hypotheses you have identified, it is likely you will use a two sample t test (as explained elsewhere on the Real Statistics website). To do this you will need two samples: one from the private sector and another from the public sector.
Charles
Actually I conducted a survey on tax saving instruments and collected 70 responses.
So now how am I supposed to do hypothesis testing on that ?
To test the hypotheses you described you need to know who in the sample is a private sector employee and who is a public sector employee. If instead your sample is made up of experts who give their opinions about such employees (or something else) then I would need more information to give an opinion as to how to proceed.
Charles
I need help!!
Describe a hypothesis test study that would help your work (Healthcare) or conclusions in some way. Describe what variable would be tested and what would be your guess of the value of that variable. Then include how the result, if the null were rejected or not, might change your conclusions or actions in some way.
Hello,
Let’s start out with the very first question. “Describe a hypothesis test study that would help your work (Healthcare) or conclusions in some way.” You need to determine this since it is based on your work.
Charles
in a research work is it possible for both the null and alternative hypothesis to be used at the same time?
Hi Dan,
Yes, they are always used at the same time, but I am not sure what the intention of your question is.
Charles
Hi Charles,
This article was extremely helpful. Written very clearly, lot of conceptual knowledge. Thank you so much. Although I have a doubt, I calculated p value for a scenario first using A/B test , then logistic regression and z – test. My p values are similar in A/B test and z- test but logistic regression gave a very different value. Can you please explain why this happens.
Hello Nidhi,
There is no reason to assume that two different tests will yield the same p-values.
Without more information about the data, the tests you used and the results, I can’t explain why you got the results you got.
Charles
Hi Charles,
I am still a bit confused regarding the null and alternative hypothesis (which we are currently studying in college). Regarding the following scenario, what would you say my findings would be if I rejected the null hypothesis? What if I failed to reject the null hypothesis?
A researcher has developed a new test to be used in diagnosis of early-stage dementia. The test involves a battery of cognitive tests, and is scored on a 100 point scale, with 100 meaning perfect cognitive function. The test is administered to 52 controls subjects, and 48 subjects who are known to have dementia. Then, the distributions of the two groups will be compared to see if the really can distinguish them.
My null hypothesis is H0: U1=U2
My alternative hypothesis is H1: U2>U1
Thank you,
Jessica
Jessica,
If you reject the null hypothesis, then you would conclude that there is a significant difference between the scores of patients being tested with those know to have dementia. I am not sure how to interpret the greater than symbol in U2 > U1 since it is not clear to me what U1 and U2 represent.
If you fail to reject the null hypothesis, then you would conclude that there is not enough evidence to reject the null hypothesis; i.e. there is not significant difference between the scores of patients being tested and those with dementia.
Charles
Imagine that a leader in Jamaica bay says that sewer runoff is causing the area to suffer lower quality water. She points to public data to make her point. One sensor in Jamaica Bay shows a mean of 3.0 after 30 samples.
Assuming the actual population mean is 3.5, is her claim about local water significant? state the null hypothesis and decide if you reject or accept it.
Aishwarya,
Based on what you read on this webpage, what do you think the null hypothesis should be?
To test this hypothesis, see the following webpages:
https://real-statistics.com/sampling-distributions/one-sample-hypothesis-testing-central-limit-theorem/
https://real-statistics.com/students-t-distribution/one-sample-t-test/
Charles
I honestly don’t understand how this is done: State the null and alternative hypotheses using statistical notation, “Individuals working under a charismatic leader will have higher task performance than will individual working under a considerate leader.”. (There were 143 students involved.)
Perhaps this is what is asked for:
Let m0 = task performance of individuals working under a charismatic leader
Let m1 = task performance of individuals working under a considerate leader
Null Hypothesis: m0 >= m1
Alt Hypothesis: m0 < m1 Charles
hi charles,
I want your help. please say me how to solve following hypothesis;
Maximum (many) people are unaware about Banking Ombudsman scheme
sample size 375, aware = 100, unaware =275, level of significance =.05
please help imitiately.
The null hypothesis as stated is too vague. You need to make it quantifiable. Perhaps you want to test whether the number of people who are unaware of the scheme is in the majority (more are unaware than aware). In this case, you can use the opposite as the null hypothesis, namely “more people are aware of the scheme than unaware”. You try to give evidence that this is not so (i.e. see whether there is a significant result).
Next you need to figure out what sort of test you can use. Hint: try using the binomial distribution (see the Real Statistics webpage for more information).
Charles
Hi Charles
Could you please help me how to state the null and alternative hypothesis with this statement,
Two political parties are debating the crime figures in Liverpool. One party, the red party, says that crime has increased compared to previous years, while the yellow party says it has not.
Many thanks!
Kristina,
Based on the webpage, what do you think the null and alternative hypotheses should be?
Charles
Hi charles please help me on my assign.
A researcher wishes to test whether modular teaching method is more effective than traditional method.how will i state my Ho and Ha?
Sarah,
The null hypothesis can take a form such as “the test score of the group that had modular teaching is equal to the score of the control group.” The alternative hypothesis (two tailed) is “the test score of the group that had modular teaching is not equal to the score of the control group.”
Charles
The human motivation theory posits that the role of the satisfaction of the basic bodily needs if of prime importance towards making an individual physically and psychologically happy. If these immediate needs are not satisfied for some reasons such as economic deprivations, the individual becomes starved and therefore, not physically able to perform his work well.
develop a null and alternative hypothesis
Nick,
Proceed as in my previous email.
Charles
Thanks!
the aboved statement what is the null and alternative hypothesis? thanks!
Man’s physical and psychological characteristics develop together at the appropriate time according to innate maturational plan. Persons with inappropriately developed psychological characteristics are likely to be influenced easily by others to engage in activities that are unacceptable to society.
develop a null and alternative hypothesis
Nick,
The null hypothesis can be stated as: The population with inappropriately developed psychological characteristics are just as easily influenced by others to engage in activities that are unacceptable to society as people who don’t have inappropriately developed psychological characteristics.
Note that you state the null hypothesis as the opposite of what you are hoping to prove. In this case, the null hypothesis is quite vague; usually you want a null hypothesis that is clear and measurable.
The alternative hypothesis is the negative (i.e. complement) of the null hypothesis and is more aligned with the original statement.
Charles
Hi Charles, I have a problem found in understanding statistics -Graham Upton , Oxford UP (p414 Q10). A have a sample of 36 pupils , proportion of the sample ofr pupil smoking at least 1 cigarette=1/3 , using a normal distr at an alpha 4% , test null H = no pupil smoked at least 1 cigarette ( so p=0 ) , and you get a mess when you want to your standard error because p =0 so sqrt(pq/n) is zero. If you have any suggestions, it would be greatly appreciated.
Tim,
I don’t really understand your null hypothesis, which I believe is equivalent to H0: No pupil smoked any cigarettes, which is clearly false if 1/3 of the pupils smoke at least one cigarette. Are you sure the scenario that you are describing is correct?
Charles
why do we need to reject the alternative hypothesis?
Mae,
We don’t need to reject the null hypothesis. The experiment is set up with the anticipation that the null hypothesis will be rejected, but that may not indeed be the results of the experiment. E.g. if you develop a new drug that cures some disease, you test that the drug is ineffective with the hope that you reject this hypothesis.
Charles
Hello Charles,
Lets assume I have the following research hypotheses:
Null Hypothesis: Men do not engage in gossips
Alternative Hypothesis: Men engage in gossips.
Assuming based some sample size, I find out that not all men engage in gossip but just a percentage of (or some) men engage in gossips (for eg, 20,30, 35 or 50). How do I conclude on the Hypotheses? Can I reject the Null Hypothesis because some men engage in gossip or is there any other test I have to do in order to arrive at a decision.
Mike,
The null hypothesis that you are using is a bit vague. When you say that men do not engage in gossip, do you mean zero? Obviously, in this case, even if one man in your sample gossiped this would refute your null hypothesis. If I replaced zero by some other value, say 1%, then I can perform a statistical test to determine whether there is a statistically significant difference between the percent of men (in the population) that gossip and 1% (two-tailed test). I could perform a statistical test to determine whether more than 1% of men (in the population) gossip with some level of confidence, say 95% (a one-tailed test).
I guess I could also replace 1% by 0%, as long as I use this sort statistical interpretation (instead of the one where one counter-example is sufficient to refute the null hypothesis).
In the situation described, I might use a proportion distribution (essentially a binomial distribution) to test my hypothesis. If say I have a sample of 100 men and 4 of them gossip, can I conclude that less than 1% of men in the general population gossip? My null hypothesis is that more than 1% gossip and I try to use my sample to gain evidence to refute the null hypothesis. In the test you assume the null hypothesis, namely that p = .01 is the probability that a man gossips and then use the binomial distribution to see how likely that in this case 4 out of 100 men in the sample gossip. Since =1-BINOM.DIST(4,100,0.01,TRUE) returns a value of .003 and that this value is much less than .05 (1-.05 is the usual 95% confidence level), we would conclude with 95% confidence that less than 1% of the men gossip. This is called a significant result.
If in our sample 2 out of 100 men gossiped, then since 1-BINOM.DIST(2,100,0.01,TRUE) = .079 > .05, we can’t conclude with 95% confidence that fewer than 1% of the men gossip.
Charles
Hello Charles,
Thanks very much for your insightful response.
can you help me solve this
1. A DTI representative wants to test at 99% level of confidence whether the average content of soda is less than 330ml as indicated in the label.
A. State the null and alternative hypothesis in words
B. State the null and alternative hypothesis in symbol
C. Probability of type error
D. Conclusions where Ho is rejected
E. Conclusions where Ho is not rejected
2. Write the null or alternative hypothesis
A. Hom = 10.2, what is Ha
B. What is Ho if Ha= m not equal to 32.6
C. What is Ho if Ha= m>45
D. What is Ho if Ha is not equal to 0.87
John,
This looks like a homework assignment. What do you think the answers to the questions are? I can help you, but you need to put some effort into this too.
Charles
Dear Dr. Zaiontz,
Thank you for such valuable information you have shared.
I have a question. I have conducted an experimental research with a null hypothesis, which was later rejected after I carried out a t-test. I am now wondering if at this stage it is possible to replace my null hypothesis with an alternative hypothesis, and then in the results section “accept or support” the alternative hypothesis? (A reviewer has asked me to do so).
Thanks a lot.
Ali,
Theoretically you could do this, but the typical statistical test that you use usually won-t accept such a change in the null and alternative hypotheses roles.
Charles
Hi Charles,
I appreciate you sharing your knowledge on statistics, but I am having trouble with a few problems.
Develop the null and alternative hypothesis for each of the following situations:
– Mr. Rogers would like to know if there is sufficient evidence to conclude that more than 60% of stocks in the NYSE increase on days that the DJIA increases.
– A company that manufactures one-half inch bolts selects a random sample of bolts to determine if the diameter of the bolts differs significantly from the required one-half inch.
– A company that manufactures safety flares randomly selects 100 flares to determine if the flares last at least 3 hours on average.
Shaneta,
These problems are very similar to the cloud seeding / rainfall example on the referenced webpage.
What do you think the answers to each of these three situations are?
Charles
I need help in writing a null and alternative hypotheses for a t-test. Could you help me?
The question was investigated of whether pleasant aromas help a student learn better. All 21 participants learned both under a condition of smelling nothing and under a condition of smelling a floral scent. Counterbalancing was followed so that some participants learned without the scent first and some learned with the scent first. All participants were apprised that the scents were “safe” and that if they wished they could leave the study at any time. Data in terms of “time (in seconds) to complete a pencil and paper maze”shown below
Heather,
See Paired t test
Charles
How do you approach a situation like this:
a. Calculate daily returns of the DJIA index and the downloaded stocks over the period under study (I have this info on a spread sheet already)
b. For each of the selected stocks and the index perform a Student’s T test, calculate the p-value and t-value and test the Null Hypothesis that the mean daily stock return is zero
for the a. I can handle but for the b. I don’t know how to approach it. Is it a paired test. independent or
Emma,
It is a one sample t test. See
One sample t test
The only problem is that the assumption of independent samples is violated since day to day there is autocorrelation,
Charles
Hello,
Can I create a T-Test with this null hypothesis, “who is less likely to stop properly at a stop sign, men or women? Or men are less likely to stop properly at a stop sign than women. What is the next step? I thank you in advance for your help.
Alex,
You can use “men are less likely to stop properly at a stop sign than women”. See the following webpage for the next step:
Two sample t test
Charles
Hi
I am an IB Psychology teacher and my students generated a directional hypothesis based on a study they were attempting to replicate. Their results were significant but in the inverse direction of the alternative hypothesis. What is the appropriate way to deal with this.
Mary,
I don’t quite know what you mean by the”results were significant but in the inverse direction of the alternative hypothesis.”
I also don’t know what you mean “deal with this”. Are you asking (1) how to interpret such a result, or (2) what to do about it, or (3) something else?
Charles
Hi Charles,
I have read all the help that you have given others and I am doing my final paper project that is due this coming Sunday and I am having a hard time with this scenario in finding the null and alternative of this scenario and I have to draw and produce a Scatterplot of the data. Here is the scenario:
What’s makes a person a leader? A social psychologist hypothesizes that the extent to which people perceived to be leaders is positively related to the amount of talking they do, regardless of what they are actually saying. She conducts an experiment in which groups of participants solve a problem together. One of the participants from each group is a confederate who speaks a different number of sentences for different groups, half of which are designed to help the groups to solve the problems and the other half are not helpful. Following the group work, the confederate is rated by the other participants on his and her leadership ability (1=low, 10=high).
What I came up with for the null hypothesis If the number of words spoken makes a person a leader (alternative) then the words that are spoken effects leadership ability.
I’m not good at this because I get mixed up with dependent and independent variable when it comes to applying my data.
In the data that I am working with you have eight groups, with the number of sentences spoken and rating of leadership here are the following data that represents the findings of this fictional research.
Number of sentences spoken
Group
1- 4
2- 10
3- 27
4- 22
5- 5
6- 6
7- 18
8- 15
Rating of Leadership
1- 5
2- 6
3- 7
4- 9
5- 2
6- 3
7- 8
8- 4
Whatever help that you can provide for me is greatly appreciated and may you have a blessed day, thank you in advance,
Barbara Lawso
Barbara,
It is not clear to me what hypothesis this test is addressing. Usually, you state your hypotheses first and then you construct the experiments necessary to gather information to support or refute the hypotheses.
It seems like you are trying to determine whether there is a difference in the ratings of the leaders based on the number of statements they make (or perhaps based on the percentage of erroneous statements). If so the null hypothesis is that there is no difference.
Charles
Dear Charles,
Sorry, If my question might sound stupid. With respect to the statement, “The hypothesis that the estimate is based solely on chance is called the null hypothesis.” What actually mean by “solely on chance”? Can you please elaborate.
Shailesh,
This is actually a pretty deep and philosophical question. Let me try responding with a simple example. If you toss a coin 1,000 times, you expect on average that 500 times heads will appear and 500 times tails. In reality an exact 500-500 split almost never happens. A split of 509-491 is probably due to chance, i.e. a random occurrence. If the split is say 809-191, this is very unlikely to be simply due to chance. The probability of such an event occurring is so low, that it make sense to suspect that the coin is biased.
Charles
Dear Charles,
Thanks for the response.
Charles,
If my mud alt hypothesis calls for a right tailed test is it possible for my t-score to be a negative number?
Lisa,
Yes, the t statistic can be negative.
Charles
Dear Charles,
I have a stupid question. I need to test H0: µ ≠ 0 against Ha: µ = 0 and get the p-value. How do I conduct such a test. Is it just 1-p-value when H0: µ = 0. And how can I specify that in Excel or Stata. Thanks
Srini,
It really depends on the specific situation, but a likely candidate is to use the one sample t test. See the following webpage for details:
One Sample t Test
Charles
My situation is in a regression context Y=AX1+BX2 and I want a nonlinear test if the ratio H0: A/B=0, that is if A=0 for non-zero values of B, then it would essentially be a joint-test of two nulls, H0: A=0 and H0: B≠0. How would I conduct this test?
Srini,
A/B = 0 is equivalent to A = 0 and B <> 0. In the webpages on multiple linear regression, you can test whether both A = 0 and B <> 0 (i.e. the X1 regression coefficient is not significant and the X2 coefficient is significant. See the webpage:
https://real-statistics.com/multiple-regression/multiple-regression-analysis/multiple-regression-analysis-excel/ (esp. Figure 3)
If there is no constant term in the regression, then you will need to use the test described in
https://real-statistics.com/multiple-regression/multiple-regression-without-intercept/
Charles
Thanks Charles for the links. Sorry I’m still a bit confused. In multiple regression, for instance Y=AX1+BX2, it is straightforward to test whether A=0 or B =0 or jointly test A=B=0. (That is, H0: The regression coefficient is NOT significantly different from zero). The regression output tables, as in Figure 3, show these test results. But, how does one test if B0 or A0 (That is, H0: whether a regression coefficient is significantly different from zero). Its basically switching H0 and Ha
Sir ,
I am HAIDER an MBA student and have to complete a research paper. My topic is ( condition of X football team). AS I know that hypothesis is an assumption(possible answer) of the research question and it has two variables dependent and independent and two hypothesis null(positive statement) and alternative (negative statement) hypothesis. Basically hypothesis create based on research question .
My research question is ( Why x football team is week?).
According to my assumption possible answer of the question would be ” x football team is week because of well coaching staff. Now i make hypothesis
Now i do my hypothesis
H1:The X football team will be strong if they hire good coaching staff.
H0:The X football team will not be strong if they hire good coaching staff. /
H0:The X football team will not be strong even if they hire good coaching staff.\
Am i right or not. What could be?
please help me.
Best regards.
Haider
IUBAT
Dhaka, Bangladesh.
Haider,
You list two null hypotheses (H0) and one alternative hypothesis (H1). Each null hypothesis should have one complementary alternative hypothesis.
Here is a potential approach:
H0: The strength of a football team is independent of the quality of its coaching staff
H1: The strength of a football team depends on the quality of its coaching staff
Essentially you are trying to support the alternative hypothesis by showing there is a significant difference between the strength of two football teams whose coaching staffs have different qualities (two tail version).
You can rephrase to make a one tailed statement.
Note that you will need to make the notions of strength and quality more precise (preferably quantifiable).
Charles
dear sir,
i am M.Phil student of bio statistics and epodemiology. yesterday i had discission with my snior. he sayr in both one tail and two tail situations the null is same mu= mu not
i say this null is true for two tailed situatiuoi only. while for one tail , in addition to equality, one has to add opposite of alternate hypothesis as well. am i right or not, nasir shah
Your view is the one that is widely held.
Charles
Dear Charles,
Please interpret the following F-test. As P-value is greater than 0.05. Are the variances equal and I should accept my Null Hypothesis?
data: org.batch1[, i] and org.batch2[, i]
F = 1.1828, num df = 149, denom df = 134, p-value = 0.322
Null Hypothesis: True ratio of variances for the two batches is equal
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.8479508 1.6450027
sample estimates:
ratio of variances
1.182792
Huma,
See the following webpage:
https://real-statistics.com/chi-square-and-f-distributions/two-sample-hypothesis-testing-comparing-variances/
Charles
Hi charles,
I am conducting reseach on franchise (fast food) & selected two samples of customers, one sample of families and the second sample of singles ( I mean university age students). The sample size of each group is 10 and level of significance of 0.05. could you please help me for developing hypothesis for following data;
Question Family singles/friends
what they have ordered?
pizza(regular) 3 2
(small) 0 4
(large) 7 4
& could you please tell me method for identifying that our data is one- tailed or two tailed.
Iqra,
The hypothesis depends on what you want to test. Only you can determine this. I am not able to look at your data and tell you what hypothesis you should use.
Charles