Worksheet Function Example
Real Statistics Function: The Real Statistics Resource Pack provides functions for calculating the confidence interval and standard error for a variety of distributions. The worksheet function for the Gumble distribution is as follows.
GUMBEL_CONF(mu, beta, n, lab, ttype, iter, alpha, fiter): returns an array with the parameter value, estimated standard error, and lower and upper limit of a 1-alpha confidence interval for the mu and beta parameters of the Gumbel distribution based on a bootstrap of iter iterations (default 1,000) for samples of size n.
ttype = 0 (MLE, default), 1 (method of moments), and 2 (pure method of moments). alpha defaults to .05. Each parameter is represented by one column with 4 rows in the output. If lab = TRUE a column of row labels and a row of column labels are appended to the results (default FALSE).
fiter is the # of iterations required to fit data to a Gumbel distribution using MLE (default 25); i.e. GUMBEL_FIT(R1, lab, fiter).
Example
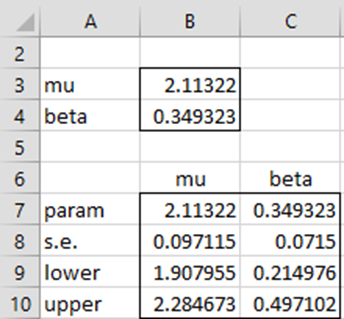
For Example 1 of Standard Error of Fitted Parameters and Example 1 of Confidence Interval of Fitted Parameters, we can use the following array formula in range A6:C10 to obtain the standard errors and 95% confidence interval for the Gumbel distribution fit parameters μ and β, based on samples of size 15, an MLE fit and 2,000 bootstrap iterations.
=GUMBEL_CONF(B3,B4,15,TRUE,,2000)
Figure 1 – Confidence intervals for fit parameters
Worksheet Functions
Real Statistics Functions: The following are the equivalent functions to GUMBEL_CONF for the other supported distributions.
BETA_CONF(alfa, beta, n, lab, ttype, iter, alpha, fiter)
EXPON_CONF(lambda, n, lab, iter, alpha)
GAMMA_CONF(alfa, beta, n, lab, ttype, iter, alpha, fiter)
GEOM_CONF(p, n, lab, ttype, iter, alpha)
LAPLACE_CONF(mu, beta, n, lab, ttype, iter, alpha)
PARETO_CONF(alfa, mn, n, lab, ttype, iter, alpha)
LOGISTIC_CONF(mu, beta, n, lab, ttype, iter, alpha, fiter)
LOGNORM_CONF(mu, sigma, n, lab, ttype, iter, alpha)
NORMAL_CONF(mu, sigma, n, lab, iter, alpha)
UNIFORM_CONF(alfa, beta, n, lab, ttype, iter, alpha, fiter)
WEIBULL_CONF(alfa, beta, n, lab, ttype, iter, alpha, fiter)
Note that ttype can also take the value 3 in WEIBULL_CONF when using the regression approach to fitting. Note too that for the NORMAL_CONF and EXPON_CONF functions, iter can also take the value zero, which indicates that a normal approximation is used (without bootstrapping). For NORMAL_CONF if iter = 0 then the critical value of the t distribution is used to find the confidence interval of the mean.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Tibshirani, R. (2014) The bootstrap. Advanced methods for data analysis
https://www.stat.cmu.edu/~ryantibs/advmethods/notes/bootstrap.pdf