Correlation testing via t test

Introduction

As in Sampling Distributions, we can consider the distribution of r over repeated samples of x and y. The following property is analogous to the Central Limit Theorem, but for r instead of x̄. This time we require that x and y have a joint bivariate normal distribution or that samples are sufficiently large. You can think of a bivariate normal distribution as the three-dimensional version of the normal distribution, in which any vertical slice through the surface of the graph of the distribution results in an ordinary bell curve.

Key Property

The sampling distribution of r is only symmetric when ρ = 0 (i.e. when x and y are independent). If ρ ≠ 0, then the sampling distribution is asymmetric and so the following property does not apply, and other methods of inference must be used.

Property 1: Suppose ρ = 0. If x and y have a bivariate normal distribution or if the sample size n is sufficiently large, then r has a normal distribution with mean 0, and t = r/s_r ~ T(n – 2) where

Here the numerator r of the random variable t is the estimate of ρ = 0 and s_r is the standard error of r.

If we solve the equation in Property 1 for r, we get

Property 1 can be used to test the hypothesis that population random variables x and y are independent i.e. ρ = 0.

Example (two-tailed)

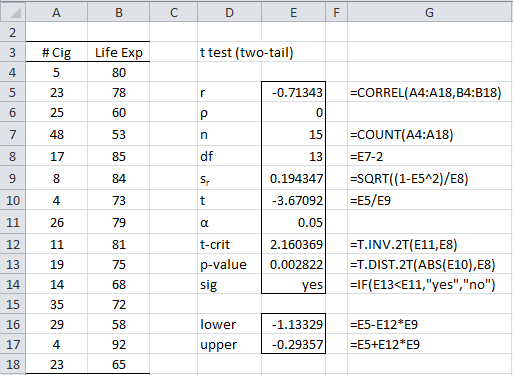
Example 1: A study is designed to check the relationship between smoking and longevity. A sample of 15 men 50 years and older was taken and the average number of cigarettes smoked per day and the age at death was recorded, as summarized in the table in Figure 1. Can we conclude from the sample that longevity is independent of smoking?

Figure 1 – Data for Example 1

The scatter diagram for this data is as follows. We have also included the linear trend line that seems to best match the data. We will study this further in Linear Regression.

Figure 2 – Scatter diagram for Example 1

Next, we calculate the correlation coefficient of the sample using the CORREL function:

r = CORREL(R1, R2) = -.713

From the scatter diagram and the correlation coefficient, it is clear that the population correlation is likely to be negative. The absolute value of the correlation coefficient looks high, but is it high enough? To determine this, we establish the following null hypothesis:

H₀: ρ = 0

Recall that ρ = 0 would mean that the two population variables are independent. We use t =  r/s_r as the test statistic where s_r is as in Theorem 1. Based on the null hypothesis, ρ = 0, we can apply Theorem 1, provided x and y have a bivariate normal distribution. It is difficult to check for bivariate normality, but we can at least check to make sure that each variable is approximately normal via QQ plots.

Figure 3 – Testing for normality

Both samples appear to be normal, and so by Property 1, we know that t has approximately a t distribution with n – 2 = 13 degrees of freedom. We now calculate

Finally, we perform either one of the following tests:

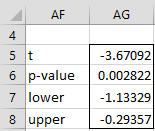
p-value = T.DIST.2T(ABS(-3.67), 13, 2) = .00282 < .05 = α (two-tail)

t_crit = T.INV.2T(.05, 13) = 2.16 < 3.67 = |t_obs |

And so we reject the null hypothesis and conclude there is a non-zero correlation between smoking and longevity. In fact, it appears from the data that increased levels of smoking reduce longevity.

Example (one-tailed)

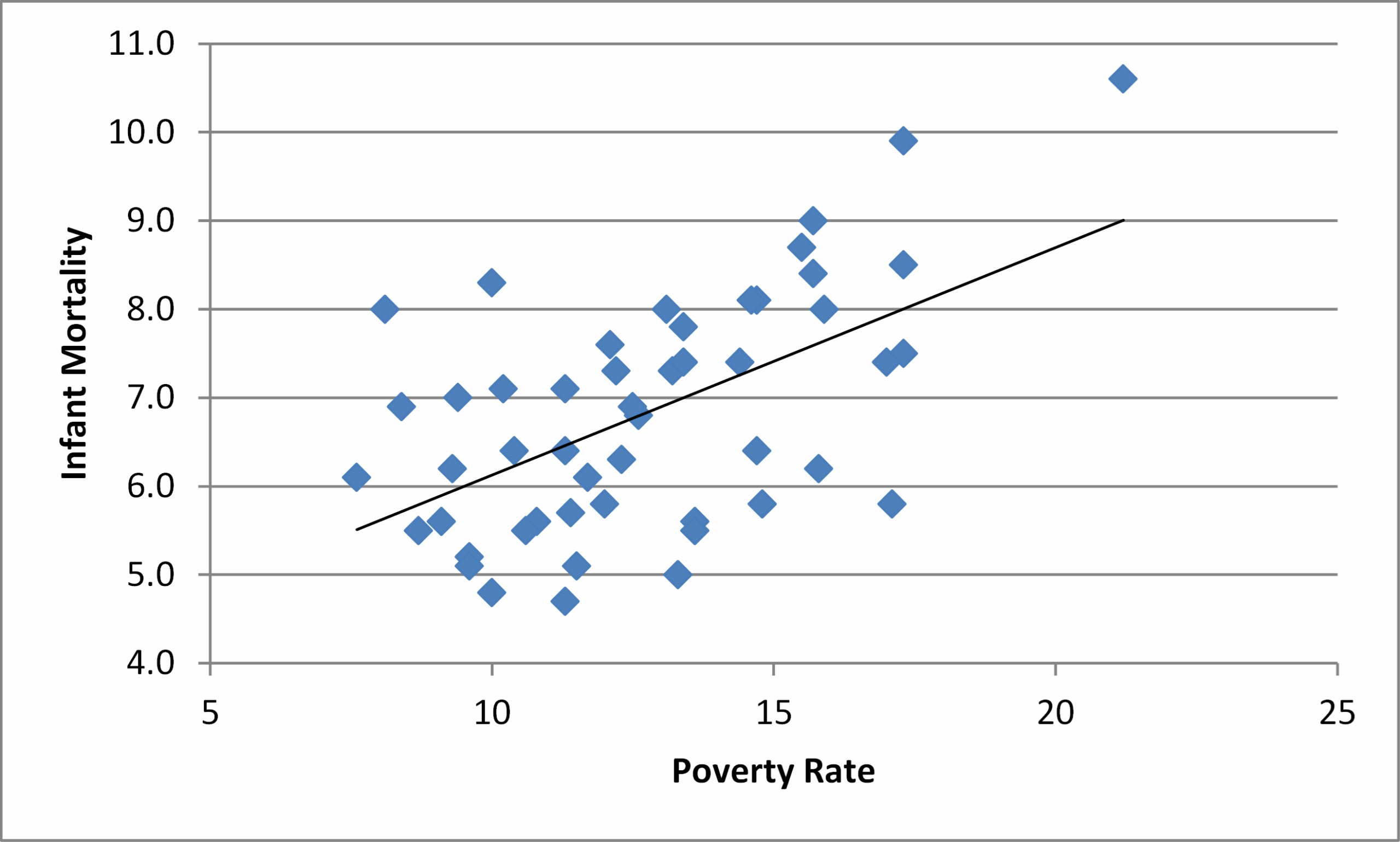
Example 2: The US Census Bureau collects statistics comparing the various 50 states. The following table shows the poverty rate (% of the population below the poverty level) and infant mortality rate per 1,000 live births) by state. Based on this data, can we conclude the poverty and infant mortality rates by state are correlated?

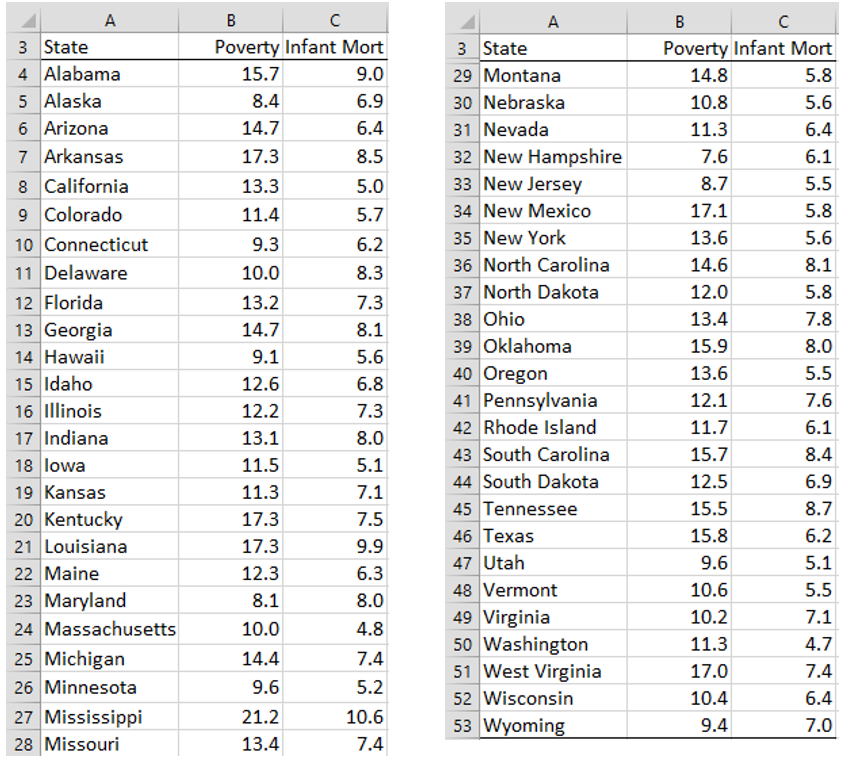
Figure 4 – Data for Example 2

The scatter diagram for this data is as follows.

Figure 5 – Scatter diagram for Example 2

The correlation coefficient of the sample is given by

r = CORREL(R1, R2) = .564

Where R1 is the range containing the poverty data and R2 is the range containing the infant mortality data. Since the population correlation was expected to be non-negative, the following one-tail null hypothesis was used:

         H₀: ρ ≤ 0

Based on the null hypothesis we will assume that ρ = 0 (best case), and so as in Example 1

Finally, we perform either one of the following tests:

p-value = T.DIST.RT(4.737, 48) = 9.8E-06 < .05 = α (one-tail)

t_crit = T.INV(.95, 48) = 1.677 < 4.737 = t_obs

Hence, we reject the null hypothesis and conclude there is a non-zero correlation between poverty and infant mortality.

Since we were confident that the correlation coefficient wasn’t negative, we chose to perform a one-tail test. It turns out that even if we had chosen a two-tailed test (i.e. H₀: ρ = 0), we would have still rejected the null hypothesis.

Worksheet Functions

Real Statistics Functions: The following functions are provided in the Real Statistics Resource Pack.

CorrTTest(r, size, tails) = the p-value of the one-sample test of the correlation coefficient using Theorem 1 where r is the observed correlation coefficient based on a sample of the stated size. If tails = 2 (default) a two-tailed test is employed, while if tails = 1 a one-tailed test is employed.

CorrTLower(r, size, alpha) = the lower bound of the 1 – alpha confidence interval of the population correlation coefficient based on a sample correlation coefficient r coming from a sample of the stated size.

CorrTUpper(r, size, alpha) = the upper bound of the 1 – alpha confidence interval of the population correlation coefficient based on a sample correlation coefficient r coming from a sample of the stated size.

CorrelTTest(r, size, alpha, lab, tails): array function which outputs t-stat, p-value, and lower and upper bound of the 1 – alpha confidence interval, where r and size are as described above. If lab = TRUE then output takes the form of a 4 × 2 range with the first column consisting of labels, while if lab = FALSE (default) then output takes the form of a 4 × 1 range without labels.

CorrelTTest(R1, R2, alpha, lab, tails) = CorrelTTest(r, size, alpha, lab, tails) where r = CORREL(R1, R2) and size = the common sample size, i.e. the number of pairs from R1 and R2 which both contain numeric data.

If alpha is omitted it defaults to .05. If tails = 2 (default) a two-tailed test is employed, while if tails = 1 a one-tailed test is employed.

Observation: For Example 1, we observe that CorrTTest(-.713, 15) = .00282, CorrTLower(-.713, 15, .05) = -1.13 and CorrTUpper(-.713, 15, .05) = -.294.

Also =CorrelTTest(A4:A18,B4:B18,E11,TRUE) produces the following output:

Critical Values

As observed earlier

We can use this fact to create the critical values for the t-test described above, namely

Real Statistics Function: The following function is also provided in the Real Statistics Resource Pack.

PCRIT(n, α, tails) = the critical value of the t-test for Pearson’s correlation for samples of size n, for the given value of alpha (default .05), and tails = 1 (one tail) or 2 (two tails), the default.

A table of such critical values can be found in Pearson’s Correlation Table.

References

Howell, D. C. (2010) Statistical methods for psychology (7^th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf

OpenStax (2023) Testing the significance of the correlation coefficient
https://stats.libretexts.org/Bookshelves/Introductory_Statistics/Introductory_Statistics_(OpenStax)/12%3A_Linear_Regression_and_Correlation/12.05%3A_Testing_the_Significance_of_the_Correlation_Coefficient