Basic Concepts
On this webpage, we provide a more detailed analysis of the between-subjects factor for Example 1 of One Between-Subjects Factor and One Within-Subjects Factor.
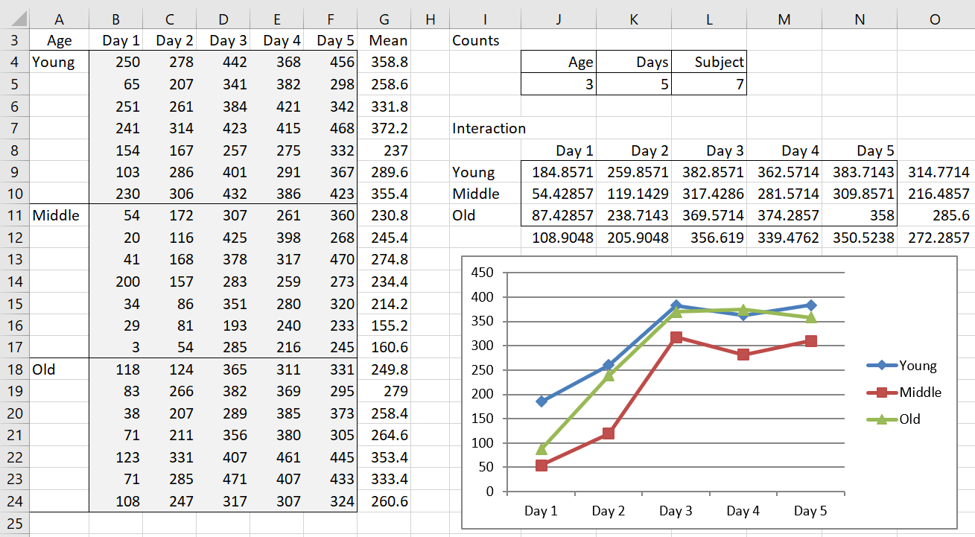
The data for Example 1 is repeated on the left side of Figure 1.
Figure 1 – Data for Example 1
One-way Repeated Measures ANOVA
Although the GG epsilon and HF epsilon are very useful in addressing sphericity issues, it is still better not to use MSE (cell Z12 in Figure 4 of One Between-Subjects Factor and One Within-Subjects Factor) as the error term in detailed analyses.
In fact, we suggest analyzing simple effects on an individual Age group basis. We do this by running a one-way repeated measures ANOVA for each Age group (or by skipping ANOVA and going directly to contrasts).
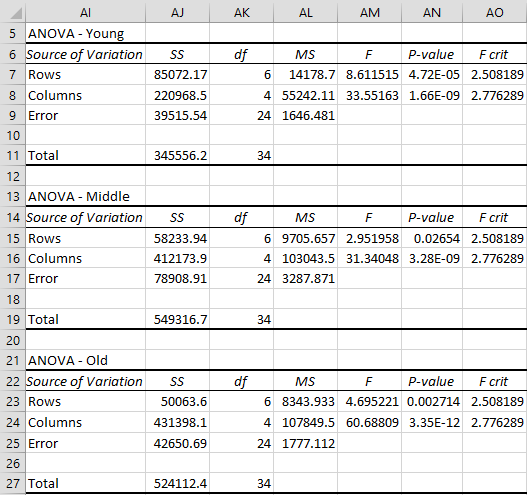
Figure 2 shows the analyses for each of the age groups (as described in ANOVA with Repeated Measures with One Within Subjects Factor).
Figure 2 – Within-subjects simple effects ANOVA
Sphericity Correction
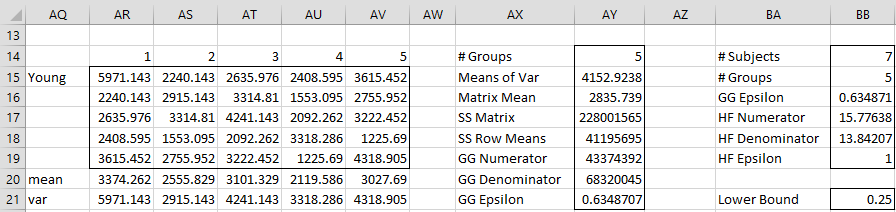
We must also compute a sphericity correction for each of these analyses based on the covariance matrices in Figure 4 of Within-Subjects Assumptions. E.g. the correction factors for the Young simple effect are shown in Figure 3.
Figure 3 – Calculation of GG and HF epsilon for Young effect
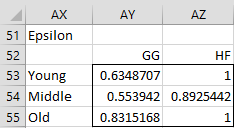
In Figure 4, we display the GG and HF epsilon values for each age group.
Figure 4 – Epsilon for each age effect
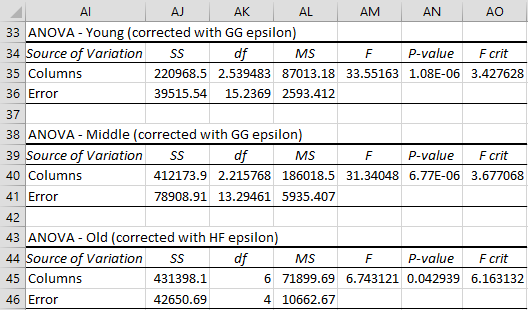
Applying the appropriate correction factor to the within-subjects ANOVA in Figure 2 (GG epsilon for Young and Middle and HF epsilon for Old), we get the revised output shown in Figure 5.
Figure 5 – Corrected within-subjects ANOVA
Note that to perform the simple effect tests, adjustments for sphericity are necessary. Equality of the covariance matrices, however, is not necessary.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf