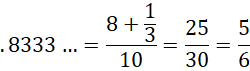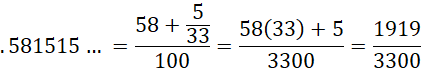Rational numbers when expressed as a decimal number can take one of two forms: (1) they have a finite number of decimal places, or (2) the decimal portion repeats endlessly. E.g. 1/2 = .5 and 3/8 = .375 are of the first form. 1/3 = .333… , 2/11 = .181818…, and 2/15 = .1333… are of the second form. Actually, the first form is a version of the second form since 1/2 = .5000… where the zeros repeat endlessly.
Conversion Approach
To convert a decimal representation of a rational number to a fraction, perform the steps shown for (1) .75, (2) .151515…, (3) .8333…, (4) .581515…
Example 1: Start by representing .75 as a fraction 75/100 (placing a power of 10 in the denominator)
Since GCD(75,100) = 25, you simplify the fraction by dividing the numerator and denominator by 25.
Example 2: First recognize that there are 2 repeating decimal places. This time you use 99 as the denominator (as many 9’s as repeating decimal places).
Since GCD(15,99) = 3, you simplify the fraction by dividing the numerator and denominator by 3.
Example 3: This example uses a combination of the techniques for Examples 1 and 2. We start with the repeating part: .333… Since there is one repeating decimal place, as in Example 2, we have
Since there is one decimal place before the repeating part, we divide by 10 (as in Example 1).
Next, we multiply the numerator and denominator by 3 (the denominator in 1/3) to obtain 25/30. Since GCD(25,30) = 5, we divide the numerator and denominator by 5 to obtain 5/6.
Example 4: Using the approach in Example 2
As we did in Example 3
Since GCD(1919, 3300) = 1, no further simplification is needed.
References
Wikipedia (2023) Repeating decimal
https://en.wikipedia.org/wiki/Repeating_decimal
Lyons, C. (2016) The secret life of 1/n: A journey far beyond the decimal point. Mathematical Enthusiast
https://scholarworks.umt.edu/tme/vol13/iss3/3