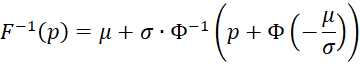Basic Concepts
A rectified normal distribution (aka rectified Gaussian distribution) is equivalent to a normal distribution N(μ,σ2) except that negative values are reset to zero. The pdf is therefore
where h(x) is the pdf of N(μ,σ2).
The cdf is therefore
Thus, the inverse function is
where Φ(x) is the cdf of N(0, 1).
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions.
RNORM.DIST(x, μ, σ, cum) = the probability density function value f(x) for the rectified normal distribution of N(μ, σ2) when cum = FALSE and the corresponding cumulative distribution function F(x) when cum = TRUE.
RNORM.INV(p, μ, σ) = the value x such that RNORM.DIST(x, μ, σ, TRUE) = p, i.e. inverse of RNORM.DIST(x, μ, σ, TRUE)
The equivalent Excel formulas are
f(x) = IF(x <= 0, 0, NORM.DIST(x, μ, σ, TRUE))
F(x) = NORM.DIST(x, μ, σ, TRUE) – NORM.DIST(0, μ, σ, TRUE)
F-1(x) = μ + σ*NORM.S.INV(p+NORM.DIST(0, μ, σ, TRUE))
Properties
The mean and variance of this distribution are
where Φ(x) is the cdf of N(0, 1) and φ(x) is the pdf of the standard normal distribution N(0, 1).
References
Beauchamp, M. (2018) On numerical computation for the distribution of the convolution of N independent rectified Gaussian variables. Journal de la Société Française de Statistique Vol. 159 No. 1.
http://www.numdam.org/item/JSFS_2018__159_1_88_0/
Wikipedia (2022) Rectified normal distribution
https://en.wikipedia.org/wiki/Rectified_Gaussian_distribution