Contingency tables with missing elements

In Independence Testing we show how to test independence using a chi-square test. We now show how to perform such a test when there is missing data (provided the data is missing at random).

Example

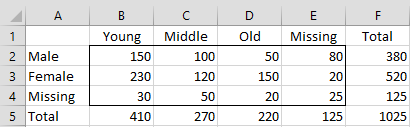
Example 1: Impute the missing data in the contingency table shown in Figure 1.

Figure 1 – Contingency Table with missing data

We partition our sample into subsets A, B, and C, in which A consists of those elements where both the row and column components are observed, B consists of those elements where only the row component is observed and C consists of those elements where only the column component is observed. Actually, there is another subset D that consists of those elements where both the row and column component is unobserved (for Example 1 there are 25 such elements, i.e. the value in cell E4). These elements are excluded from the analysis.

The completed contingency table, therefore, contains entries x_ij where

Here is observed, but  and  are not. The marginal totals are x_i = and x_j = where the completed contingency has r rows and c columns (r = 2 and c = 3 for Example 1).

We also define and . Note that the values $latex x_{ij}^A$, latex x_j^C$ are observed.

EM Algorithm

Essentially we have a multinomial distribution with parameters p = {p_ij: i ≤ r and j ≤ c}. Our goal is to find the values of p_ij that minimize LL based on the observed data. Initially, we can set p_ij = 1/(rc) (initial M step). The algorithm works as follows:

E step: estimate the values of the  based on the observed data and the current estimates of the p_ij (from the previous M step):

M step: estimate the values of the  based on the observed data and the current estimates of the x_ij (from the previous E step):

 

The two steps can be combined so that new values of the p_ij (at step k+1) can be estimated from the previous values of the p_ij (at step k) by

EM Algorithm for Example 1

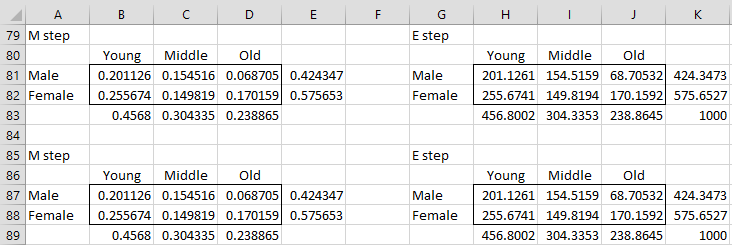
For Example 1, the analysis begins as shown in Figure 2.

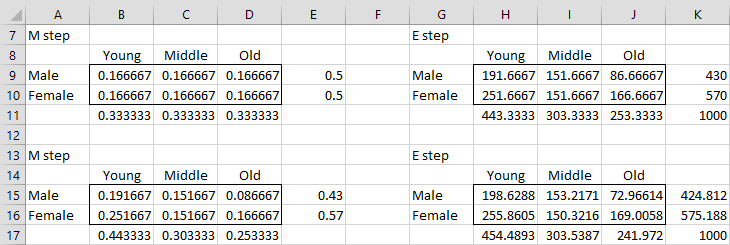
Figure 2 – EM algorithm (iterations 1 and 2)

The six cells in range B9:D10 contain the initial M step values of p_ij = 1/6 (for a total of 1). Cell H9 (representing the initial data value x₁₁) contains the worksheet formula =$B$2+$E$2*B9/E9+$B$4*B9/B11 (and similarly for the other cells in range H9:J10, for the first E step). Range B15:D16 contains the array formula =H9:J10/K11 (second M step).

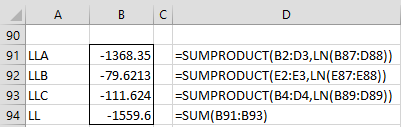
The proceeding E and M steps are calculated in the same way. After 14 steps we arrive at the results shown in Figure 3, demonstrating convergence.

Figure 3 – Convergence of EM algorithm

Thus, we see that we can apportion the missing data as shown in range H81:J82. We can also obtain estimated p_ij values as shown in range B81:D82.

We now calculate the maximum log-likelihood value based on this result. This value is based on the partition consisting of A, B, and C, as follows:

where

We obtain the maximum log-likelihood estimate of -1,559.6, as calculated in Figure 4.

Figure 4 – Maximum log-likelihood estimate

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Ehlers, R. (2005) Incomplete contingency tables
No longer available online

Howell, D. (2008) The treatment of missing data
https://www.uvm.edu/~statdhtx/StatPages/Missing_Data/MissingDataFinal.pdf