Property A: For a random variable x, the variance of g(x) can be approximated by
Proof: The proof uses the Delta method, namely from the Taylor series for any constant a, we have
Now, let a = mean of x. Then
since var(y+c) = var(y), var(c) = 0, and var(cy) = c2 ⋅ var(y) for any y and constant c (by Property 3 of Expectation).
Property 1 (Greenwood): The standard error of S(t) for any time t, tk ≤ t < tk+1 is approximately
Proof: First we note that
where pj = 1 − dj/nj the probability that a subject survives to just before tj. Taking the natural logs
We now assume that the number of subjects that survive in the interval [tj, tj+1) has a binomial distribution B(nj, πj) where pj is an estimate for πj. Since the observed number of subjects that survive in the interval is nj − dj, it follows (based on the variance of a binomial random variable) that
Based on Property A
Thus
But using Property A again, we also have
Taking the square root of both sides of the equation completes the proof.
Property 2: The approximate 1−α confidence interval for S(t) for t, tk ≤ t < tk+1, is given by the formula
where zα/2 = NORM.S.INV(1−α/2).
Proof: We could use a confidence interval of S(t) ± zα/2 ⋅ s.e., but it has the defect that it can result in values outside the range of S(t), namely 0 to 1. Thus it is better to use a transformation that transforms S(t) to the range (-∞,∞) and then take the inverse transformation. We use the transformation ln(−lnx) to accomplish this. This transformation is defined for x = S(t), except when S(t) = 0 or 1.
By Property A
From this and the proof of Property 1, it follows that
Thus the standard error of ln(-ln S(t)) is
The result now follows by taking the inverse transformations.
Proof: By definition
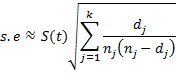
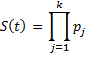
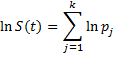
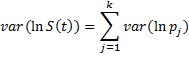
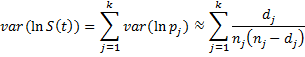
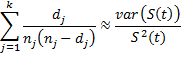
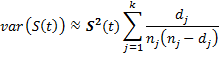
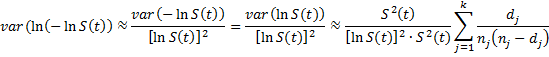
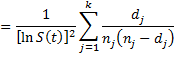
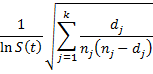
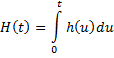
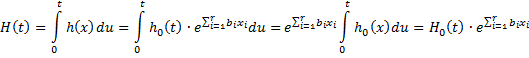
Hi
Thanks for a most useful website.
Regarding Property A, shouldn’t Var(g(X))≈[g'(X)]^2*Var(X) be Var(g(X))≈[g'(E(X)]^2*Var(X) since Var(cY)=c^2*Var(Y)? If this is not the case, please explain.
Yes, you are correct. Var(cY)=c^2*Var(Y).
Thanks for identifying this error.
Charles