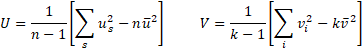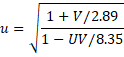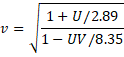PROX Model for Rasch Analysis

Objective

We now describe another approach for building a Rasch model that is based on the simplifying assumptions that the ability and difficulty parameters are normally distributed; in particular, we assume that the ability parameters are normally distributed.

Notation

Suppose that we have test data with values x_si as defined in Basic Concepts for Rasch Analysis, except that now we will allow scores of 0, 1, 2, …, m where m is any positive integer including values larger than 1. Assume that there are n subjects and k items.

For any subject s, define

If there are no missing scores then k_s = k for all s. For any item, in a similar way, define

The means and variances of the u_s and v_i are

Ability parameter estimates

It turns out that we can approximate the β_s ability parameter for subject s by

where u is the scaling factor

Here, 2.89 = 1.7² and 8.35 = 1.7⁴.

If we attempt to approximate the normal distribution cdf F(x) by the logistic distribution cdf G(x) = 1/(1+e^–ax), then we achieve the best such approximation when a = 1.7 (actually 1.702). Here, best means the value of a for which max |F(x) – G(x)| is minimized. This is why we used the factor 1.7 in the above formula.

Difficulty parameter estimates

It also turns out that we can approximate the δ_i difficulty parameter for item i by

where v is the scaling factor

Here, the mean of the v_i is subtracted from each v_i term to center the difficulty parameters as was done in the UCON method described in Building a Rasch Model.

Standard estimates

In addition, estimates for the standard errors of the ability and difficulty parameters are

References

Wright, B. D. and Stone, M. H. (1979) Best test design. MESA Press: Chicago, IL
https://research.acer.edu.au/measurement/1/

Wright, B. D. and Masters, J. N. (1982) Rating scale analysis. MESA Press: Chicago, IL
https://research.acer.edu.au/measurement/2/