Confidence Hyper-ellipse and Eigenvalues

As we observe in Multivariate Normal Distribution Basic Concepts, the 1–α hyper-ellipse plays a similar role to the confidence interval in univariate statistics. We now describe some additional characteristics of these hyper-ellipses, and in particular, their relationship with eigenvalues.

Basic Properties

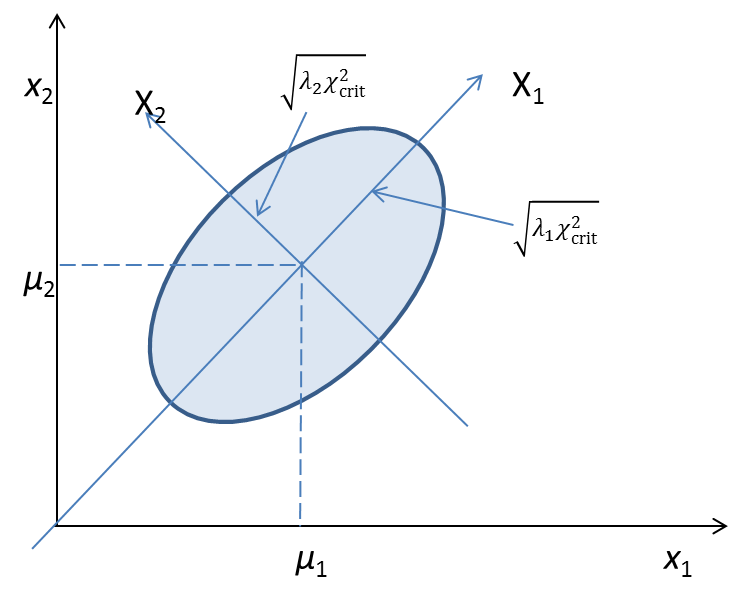
The axes of the ellipse have lengths that are a function of the eigenvalues of the Σ. Also, each axis is in the direction of the eigenvector corresponding to one of the eigenvalues.

Figure 1 – Confidence ellipse

The half-length of the axis corresponding to eigenvalue λ is given by the formula

where is the critical value for χ²(k).

All these properties extend to the case where k > 2. In this case, we speak of hyper-ellipses (or ellipsoids) instead of ellipses.

The volume of the hyper-ellipse (or area in the case where k = 2) is given by the function

Note too that by Property 1 of Eigenvalues and Eigenvectors, |Σ| = product of the eigenvalues of Σ.

Example

Example 1: Calculate the eigenvalues and eigenvectors of the sample covariance matrix for Example 1 of Descriptive Multivariate Statistics.

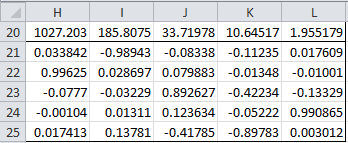
Figure 2 – Eigenvalues and eigenvectors for Example 1

Using the Real Statistics array function eVECTORS(H5:L9) we can generate the output displayed in Figure 2. Alternatively, we can get the same result by using the Real Statistics Matrix data analysis tool (as described in Matrix Operations and Real Statistics Data Analysis Tools) and choosing the Eigenvalue/eigenvector option. The top row of Figure 2 lists the 5 eigenvalues. Below each eigenvalue is a corresponding unit eigenvector.

As noted above, the half-lengths of the axes corresponding to the eigenvalues are

where is the critical value for χ²(5).

Using the sample covariance matrix as an approximation for the population covariance matrix and the eigenvalues obtained in Figure 2, the lengths of these axes are:

Figure 3 – Axes lengths for Example 1

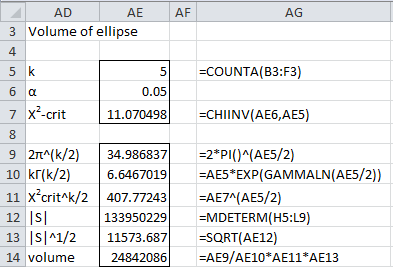
The volume of the 95% confidence ellipse is 24,842,086 calculated as follows:

Figure 4 – Volume of 95% confidence ellipse for Example 1

Note that |S| (cell A12) can also be calculated as the product of the five eigenvalues.

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following functions

CONF_MNORM(R1, alpha, iter): array function that returns a column array with the lengths of the axes in the 1-alpha confidence ellipse based on the data in R1

CONF_VOLUME(R1, alpha, iter): returns the volume (area if R1 only has two columns) of the 1-alpha confidence ellipse based on the data in R1.

The default of alpha is .05. iter = # of iterations in calculating eigenvalues (default 100).

For Example 1, the output from =CONF_MNORM(B4:F30) is the transpose of range X4:AB4 of Figure 4. The output from =CONF_VOLUME(B4:F30) is the value in cell U18.