Basic Concepts
In Example 1 of Multiple Regression Analysis we used 3 independent variables: Infant Mortality, White, and Crime, and found that the regression model was a significant fit for the data. We also commented that the White and Crime variables could be eliminated from the model without significantly impacting the accuracy of the model. We can use the following property to test whether all of these variables add significantly to the model.
where m = number of independent variables being tested for elimination and SS’E is the value of SSE for the model without these variables.
E.g. suppose we consider the multiple regression model
and want to determine whether b3, b4, and b5 add significant benefit to the model (i.e. whether the reduced model y = b0 + b1x1 + b2x2 is significantly no worse than the complete model). The null hypothesis H0: b3 = b4 = b5 = 0 is tested using the statistic F as described in Property 1 where m = 3 and SS’E reference the reduced model, while SSE, MSE, and dfE refer to the complete model.
Example
Example 1: Determine whether the White and Crime variables can be eliminated from the regression model for Example 1 of Multiple Regression Analysis.
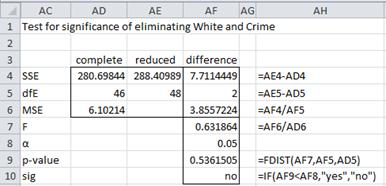
Figure 1 implements the test described in Property 1 (using the output in Figure 3 and 4 of Multiple Regression Analysis to determine the values of cells AD4, AD5, AD6, AE4 and AE5).
Figure 1 – Determine if White and Crime can be eliminated
Since p-value = .536 > .05 = α, we cannot reject the null hypothesis, and so conclude that White and Crime do not add significantly to the model and so can be eliminated.
Alternative Approach
An alternative way of determining whether certain independent variables are making a significant contribution to the regression model is to use the following property.
where R2 and dfE are the values for the full model, m = number of independent variables being tested for elimination and is the value of R2 for the model without these variables (i.e. the reduced model).
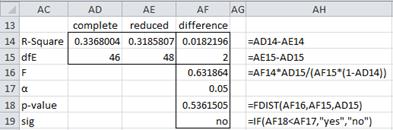
If we redo Example 1 using Property 2, once again we see that the White and Crime variables do not make a significant contribution (see Figure 2, which uses the output from Figures 3 and 4 of Multiple Regression Analysis to determine the values of cells AD14, AD15, AE14, and AE15).
Figure 2 – Using R-square to decide whether to drop variables
When there are a large number of predictors
When there are a large number of potential independent variables that can be used to model the dependent variable, the general approach is to use the fewest number of independent variables that accounts for a sufficiently large portion of the variance (as measured by R2). Of course, you may prefer to include certain variables based on theoretical criteria rather than using only statistical considerations.
If your only objective is to explain the greatest amount of variance with the fewest independent variables, generally the independent variable x with the largest correlation coefficient with the dependent variable y should be chosen first. We can then add additional independent variables until we achieve the desired level of accuracy.
In particular, the stepwise estimation method is as follows:
- Select the independent variable x1 which most highly correlates with the dependent variable y. This provides the simple regression model y = b0 + b1 x1
- Examine the partial correlation coefficients to find the independent variable x2 that explains the largest significant portion of the unexplained (error) variance) from among the remaining independent variables. This yields the regression equation y = b0 + b1 x1 + b2 x2.
- Examine the partial F value for x1 in the model to determine whether it still makes a significant contribution. If it does not then eliminate this variable.
- Continue the procedure by examining all independent variables not in the model to determine whether one would make a significant addition to the current equation. If so, select the one that makes the highest contribution, generate a new regression model and then examine all the other independent variables in the model to determine whether they should be kept.
- Stop the procedure when no additional independent variable makes a significant contribution to the predictive accuracy. This occurs when all the remaining partial regression coefficients are non-significant.
Motivation
From Property 2 of Multiple Correlation, we know that
Thus we are seeking the order x1, x2, …, xk such that the leftmost terms on the right side of the equation above explain the most variance. In fact, the goal is to choose an m < k such
Alternative Approach
We can use the following alternatives to this approach:
- Start with all independent variables and remove variables one at a time until there is a significant loss in accuracy
- Look at all combinations of independent variables to see which ones generate the best model. For k independent variables, there are 2k such combinations.
Since multiple significance tests are performed, when using the stepwise procedure it is better to have a larger sample space and to employ more conservative thresholds when adding and deleting variables (e.g. α = .01). In fact, it is better not to use a mechanized approach and instead evaluate the significance of adding or deleting variables based on theoretical considerations.
Note that if two independent variables are highly correlated (multicollinearity) then if we use one of these in the model, it is highly unlikely that the other will enter the model. One should not conclude, however, that the second independent variable is inconsequential.
Observation: In Stepwise Regression, we describe another stepwise regression approach, which is also included in the Linear Regression data analysis tool.
Using AIC and SBC
In the approaches considered thus far, we compare a complete model with a reduced model. We can also compare models using Akaike’s Information Criterion (AIC).
Definition 1: For multiple linear regression models, we define Akaike’s Information Criterion (AIC) by
When n < 40(k+2) it is better to use the following modified version
Another such measure is the Schwarz Bayesian Criterion (SBC), which puts more weight on the sample size.
All things being equal it is better to choose a model with lower AIC, although given two models with similar AICs there is no test to determine whether the difference in AIC values is significant.
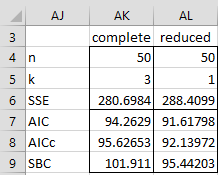
Example 2: Determine whether the regression model for Example 1 with the White and Crime variables is better than the model without these variables.
Figure 3 – Comparing the two models using AIC
Since the AIC and SBC for the reduced model are lower than the AIC and SBC for the complete model, once again we see that the reduced model is a better choice.
Observation: AIC (or SBC) can be useful when deciding whether or not to use a transformation for one or more independent variables since we can’t use Property 1 or 2. AIC is calculated for each model, and all other things being equal the model with the lower AIC (or SBC) should be chosen.
Observation: Augmented versions of AIC and SBC, used in some texts, are as follows:
![]()
![]()
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following worksheet functions where R1 is an n × k array containing the X sample data and R2 is an n × 1 array containing the Y sample data.
RegAIC(R1, R2,, aug) = AIC for the regression model for the data in R1 and R2
RegAICc(R1, R2,, aug) = AICc for regression model for the data in R1 and R2
RegSBC(R1, R2,, aug) = SBC for the regression model for the data in R1 and R2
If aug = FALSE (default), the first version of AIC, AICc, SBC are returned, while if aug =TRUE, then the augmented versions are returned.
We also have the following Real Statistics function where R1 is an n × k array containing the X sample data for the full model, R2 contains the X sample data for the reduced model and Ry is an n × 1 array containing the Y sample data.
RSquareTest(R1, R2, Ry) = the p-value of the test defined by Property 2
Thus for the data in Example 1 (referring to Figure 2 of Multiple Regression Analysis), we see that the value of RegAIC(C4:E53,B4:B53) is 94.26, RegAICc(C4:E53,B4:B53) = 95.63 and RSquareTest(C4:E53,C4:C53,B4:B53) = .536.
There is also the following expanded version of this Real Statistics function:
RSquare_Test(R1, R2, Ry, lab): returns a 6 × 1 column array with values R-square for the full model, R-square for the reduced model, F, df1, df2, and the p-value of the test of the significance of X data in R2 (reduced model) vs. X data in R1 (full model) where Ry contains the Y data. If lab = TRUE (default FALSE) then a column of labels is appended to the output.
Observations
This webpage focuses on whether some of the independent variables make a significant contribution to the accuracy of a regression model. We can use the same approach to determine whether interactions between variables of the square or higher orders of some variables make a significant contribution.
You can also ask the question, which of the independent variables has the largest effect? There are two ways of addressing this issue.
- You standardize each of the independent variables (e.g. by using the STANDARDIZE function) before conducting the regression. In this case, the variable whose regression coefficient is highest (in absolute value) has the largest effect. If you don’t standardize each of the variables first, then the variable with the highest regression coefficient is not necessarily the one with the highest effect (since the units are different).
- You rerun the regression removing one independent variable from the model and record the value of R-square. If you have k independent variables you will run k reduced regression models. The model which has the smallest value of R-square corresponds to the variable which has the largest effect. This is because the removal of that variable reduces the fit of the model the most.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
Hi Charles,
I have a question about partial and semi partial correlation. I saw on web that partial regression coefficients similar to semi-partial and not to partial correlation. I really do not understand that.
On the one hand, in calculating the significance of an IV in simultaneous MLR , we refer to the effect of each IV on the residual variance of the DV and not on the total variance as semi-partial does. In addition when we take the residuals of y~X2 and X1~X2 and run simple linear regression the partial coefficient we get is equal to partial correlation. On the other hand, the formula of the standardized coefficient (Beta) and the semi-partial correlation are very similar except the square root in the denominator.
I would greatly appreciate your answer to my question
best regards,
Avshalom
What is your question?
Charles
Do partial regression coefficients in MLR base on partial or semi-partial correlations?
when calculating the significance of the partial regression coefficients in MLR, do we
residualize Y each time we add another IV?
Hello Avshalom,
1. I suggest that you carry out a linear regression with 2 independent variables and then see for yourself whether the coefficients are baed on partial or semi-partial correlations using the formulas described at
https://real-statistics.com/correlation/multiple-correlation/
2. I don’t know what you mean by “residualize Y”, If you add another IV, then the residuals will change.
Charles
Hi Charles,
In respect of the AIC and BIC values, I understand that the smaller the value the better the model.
Is that also the case for negative AIC/BIC values though? In which case larger negative values indicate the better model, or is it the smaller absolute value that indicates the better model?
Many thanks,
Gareth
Hi Gareth,
I think that is the smaller value even if negative.
Charles
Hi,
I had a confusion regarding the determination of the greatest impact of independent variables on the dependent variable. To find out the greatest predictor do I analyse the path coefficients or the p-value?
See https://www.real-statistics.com/multiple-regression/shapley-owen-decomposition/
Charles
You mention that the size of the effect of variables could be determined by the comparing coefficients if the data are first standardized. Since standardizing involves dividing by the standard deviation of each variable, wouldn’t this be equivalent to comparing after the regression by just multiplying each coefficient by the standard deviation of the corresponding variable? This is similar to a parameter that has been called the importance ratio (I.R.), a normalized sensitivity. I have discussed the I.R. in this paper: DOI: 10.1061/(ASCE)EE.1943-7870.0000216.
Hi David,
To standardize you need to first subtract the mean and then divide by the standard deviation.
Charles
Hi Charles,
I am working with a large data set that has several categorical variables. I will use your categorical coding method to code these. My question is whether I should standardize the coded variables as well as the interval variables so that I can use the r-squared as a gauge on variable impact on the model? We want to include as much data in the model as is helpful in building a strong predictor.
Cheers!
Jerry
Hello Jerry,
I don’t see any advantage of standardizing any of the variables. You can use the R-square value even if you don’t standardize.
Charles
Charles,
Thanks for the response. I have been enjoying the website and truly appreciate your efforts in building it!
Jerry
Hi,
I would be happy if I get an answer to my question on the multiple regression. My question is that: can we keep an insignificant variable in the model if the model suffers from excluding this variable?
The output is following:
Coefficient p-value
const 37225.5 0.0359 **
X1 −12.0859 <0.0001 ***
X2 2535.05 0.0002 ***
X3 −1613.09 0.0019 ***
X4 0.369741 0.3808
Mean dependent var 5325.527 S.D. dependent var 17210.62
Sum squared resid 92855453 S.E. of regression 3933.943
R-squared 0.968652 Adjusted R-squared 0.947753
F(4, 6) 46.34945 P-value(F) 0.000120
Log-likelihood −103.3260 Akaike criterion 216.6519
Schwarz criterion 218.6414 Hannan-Quinn 215.3978
rho 0.002316 Durbin-Watson 1.849753
White's test for heteroskedasticity – Null hypothesis: heteroskedasticity not present
p-value = 0.564975
Test for normality of residual – Null hypothesis: error is normally distributed
p-value = 0.830419
LM test for autocorrelation up to order 1 – Null hypothesis: no autocorrelation
p-value = 0.993416
RESET test for specification – Null hypothesis: specification is adequate
p-value = 0.560848
There is no multicollinearity as well
Firuza,
You can certainly keep an insignificant variable in the model. This can be useful when removing the variable causes one or more of the assumptions to be violated.
Charles
I need to predict sales on basis of promotion and i have past 3 months sales data and promotion cycle of each month.i do have next month promotion file for which i need to predict sales.how shall i initiate and how intearction variable will work here.please help!
Rushi,
You have a number of choices here. You could use regression (linear, polynomial, exponential, etc.) or some form of time series analysis (Holt-Winter, ARIMA, etc.). These approaches are described in various parts of the website.
Before you start, I suggest that you create a scatter chart (as described on the website) to see whether your data has a linear or some other pattern. You can also see whether there is any seasonality element to the data. This will help you decide which technique to use.
Charles
Hi
I have the following problem
1. My class has 30 students
2. Outcome variable is grade on test of French language coded as pass or fail (binary outcome)
3. There are 3 different models that can predict success of failure of each student
4. Which test can be employed to determine which is the best model for prediction?
Arshad,
It depends on how you define “best”. If you mean the least squared error, then for each model you calculate for each of the 30 students the square of y-observed minus y-predicted by the model and then sum these values. The model that has the smallest value for this sum of squares can be considered the best. There are other criterion that can be used though.
Charles
I performed a stepwise logistic regression analysis with ~100 total data points and ~30 outcomes of interest. With respect to the “one in ten rule of thumb” is there a maximum number of independent variables I can test in a stepwise fashion?
There are at most three variables in my final model. Did I err if, say, I tested a dozen variables to choose those 3 in the final model? I never really thought about overfitting in this scenario, to be honest.
I can tell you more specifics of the data if necessary.
Claire,
I don’t recall describing a “one in ten rule of thumb”. What exactly is this rule? I don’t know any maximum number of independent variables that can be tested in a stepwise fashion.
Have you looked at the following webpage?
Stepwise Regression
Charles
these helped me a lot in my assignment. thanks!
Glad I could help.
Charles
Hi Charles
Kindly advise me on the following:
1. I have three independent variables (AT, SY & PC) which are all significant to the dependent variable C. The only distinction is that the Variable AT’s coefficient is negative whereas the others are positive. How should I explain this?
2. The KMO for the factorization is above 50% ie, .593 which also means that it is acceptable. How should I explain this in regard to the study.
I am not a statistics person so I am very ‘hot’.
Thank you for your consideration
Peter,
1. The fact that some coefficients are positive or negative has nothing to do with whether the corresponding variable is significant.
2. See https://real-statistics.com/multivariate-statistics/factor-analysis/validity-of-correlation-matrix-and-sample-size/
Charles
Charles, your website is fantastic, I appreciate this resource being freely available online in such a clear and coherent format.
Thank you Liz,
Charles
Hi Charles,
Would you please help with the interpretation of this multiple regression output. I was appointed Headteacher of Chipembi Girls’ Secondary School, in 2010, at the time when the overall school performance and that of Maths, Science and Biology were plummeting.
I invested hugely to improve the quality of teaching and learning in the aforementioned subjects and the overall school performance dramatically improved (as shown below). I wanted to determine the impact of the three subjects (Maths, Science and Biology) in improving the schools overall Grade 12 pass rate.
YEAR SCH % PASS % FAIL – MATHS % FAIL BIOLOGY % FAIL – SCIENCE
2009 91.8 29 14 17
2010 98.44 23 0.78 7
2011 99.22 10.9 4.7 1.6
2012 99.3 8.1 2.9 7.4
2013 100 9.4 0 4
2014 100 8.4 0 2.52
2015 100 4.7 0 0.94
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.985741155
R Square 0.971685624
Adjusted R Square 0.943371247
Standard Error 0.705417301
Observations 7
ANOVA
df SS MS F Significance F
Regression 3 51.23093072 17.07697691 34.31774775 0.008019283
Residual 3 1.49284070 0.497613568
Total 6 52.72377143
Coefficients Standard Error t Stat P-value
Intercept 101.2674647 0.537506587 188.4 3.29737E-07
% FAIL – MATHS -0.076790072 0.060340374 -1.272 0.292830347
% FAIL BIOLOGY -0.323322932 0.105568695 -3.062 0.054877288
% FAIL – SCIENCE -0.140791256 0.125626235 -1.121 0.344033995
Questions:
1. What is the meaning of R squared in this context, i.e. as regards the effect size of Maths, Science and Biology?
2. Since both Maths & Science P-values were insignificant, would it right to say that both subjects did not contribute to the general improvement in the overall school performance?
3. Would I be right to attribute the 97% variation in the dependent variable as being solely influenced by Biology?
Thanking you in advance for assistance.
Regards,
Albert
Albert,
1. I don’t know how to relate R squared to the effect size of Math, Science and Biology.
2. Yes, Math and Science did not make a significant improvement based on this model. However, I would next test the models (1) Math and Biology and (2) Science and Biology to see whether the p-value is still insignificant.
3. No, if you remove Math and Science the R-square value will go down. These variables make a difference, but the difference is not significant.
Charles
Charles:
I am doing a 90 day electricity consumption study on two buildings. I took daily meter readings (t morning and night). I have run simple linear regressions in excel to determine with low, high or average temperature where the better predictive value. In this simple two variable regression, the average temp. had the highest r2, and therefore, is the better predictive independent variable correct?
Now the important question. I have found that consumption on Friday drops consistently from previous days (people leave early and actually turn off air, lights, and computers. How do i set up a regression analysis taking into account the temperature and the day of the week?
Julio,
I am not sure what you mean by average temperature has the better predictive variable. Temperature is the variable.
What you are describing in paragraph two is a version of seasonal regression. Please see the following webpage for how you add day into the regression model: Seasonal Regression
Charles
Hi Sir,
I am working on estimation of permeability using different well responses using multivariate regression analysis.
What is the relation the of null hypothesis with p value and alpha?
Is this possible that variable having highest regression coefficient may have lowest significance in multivariate regression analysis?
Thanks a lot for your time.
Hi Atif,
See the following webpage regarding your first question:
Null and Alternative Hypothesis
Yes it is possible that the highest regression coefficient has the lowest significance.
Charles
Hi Charles,
Great information as always.
Quick question: what are the benefits of using this method to determine the significance of a variable vs. using the t-stat for the slope of the line?
The latter seems more straightforward and easier to implement so it’d be useful to know when I ought to switch to this instead.
Thanks,
Jonathan
Jonathan,
The t stat is sufficient if you want to determine whether one variable is making a significant contribution to the model. If you want to see whether two or more variables together are making a significant contribution, then you should use the other approach. Also the other approach can be used to determine relative contributions of each variable.
Charles
Hi,
I am stuck with the following:
4 independent variables,
1 dependent variable, (i.e. Y= a+x1+x2+x3+x4 + E
After running the regression using SPSS, the following were the result:
R² =0.899
F change= 55.448
Sig. (signicant)= 0.000
But, the Beta coefficients are:
a= 1606.175
X1 = 2.477 sig. @ 0.001
X2 = 0.085 sig. @0.001
X3 = 0.00001664 sig. @0.079
X4 = – 0.023 sig. @ 0.000.
Considering the beta coefficients, can I say the Independent variables have contributed significantly to the dependent at 5% Significance level.
Sorry for the error in the earlier message.
Looking forward to a prompt response. Good job out here.
If I understand the results you obtained correctly, then the only variable that didn’t make a significant contribution is X3 (since .079 > .05).
Charles
Many Thanks, Charles
Hi there!
I am stuck on a regression where both my independent variables are significant. what does this mean now?
Ella,
It means that both independent variables are contributing to the linear regression (i.e. the corresponding coefficients are significantly different from zero).
Charles
Hi if I were to use a regression (OLS for univariante and multivariante cases) to determine the “weight” or significant variables affecting this, what statistics should be examined?
Thanks
Alberto
Alberto,
I don’t completely understand your question, but perhaps you are looking for the Shapley-Owen.
Charles
i have three independent variables which is x1,x2,x5 i want formula for R. PLEASE help
Sorry Martha, but I am not sure that I understand your question. Perhaps the answer to your question can be found on the webpage
Advanced Multiple Correlation Coefficient
Charles
nice course i like it. i have one research the topic was determinants of tax revenue performance w/c model is preferably to this study?
Asmara,
Sorry, but I don-t understand your question.
Charles
Can you comment on the AIC correction that you use. In reviewing Burnham and Anderson 2002, they provide the correction as AICc= AIC + [(2K(K+1))/(n-K-1)]. I was looking for a reference to the correction you use here. Thanks.
Tim,
It all depends on what k is. I understood that in the formula that you are using, k includes all the model parameters. These are the variables, intercept and variance. In the formula I am using k = the number of independent variables, and so I need to add 2 for the intercept and variance parameters.
There is a discussion of these issues on the following website
http://stats.stackexchange.com/questions/69723/two-different-formulas-for-aicc
I believe that the formula I am using is consistent that found on the website
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.506.1715&rep=rep1&type=pdf
Charles
i need to solve the question pls. help me
y – Production of beef in kg/ha;
x1- Average quantity of potatoes (kg)
intended for the animal feed within 1 day;
x2- The farm size in hectares;
x3- The average purchase price of beef in a
given region (in zł/kg);
x4- Number of employed persons on the
farm.
y x1 x2 x3 x4
1950 20 10 5 4
2200 24 13 5,4 4
2600 25 15 5,6 5
2900 33 20 5,2 6
3000 32 20 5,3 7
3750 38 25 5,8 7
4900 49 30 6 9
5100 50 35 5,2 9
5800 60 37 5,9 10
Based on data from nine farms build a linear econometric model. Perform appropriate
statistical tests (F test and t-Student tests) , remove an independent variable and recalculate
the model if necessary
To build the multiple linear regression model see the Multiple Regression webpage. You can perform this analysis manually, using Excel or using the Real Statistics tools. To determine what happens when you remove one independent variable, see the referenced webpage.
Charles