Schur’s Factorization

Introduction

In QR Factorization, we show how to construct a QR factorization for any invertible square matrix A (with real elements). In fact, we can use the QR Factorization option of the Matrix data analysis tool to calculate the orthonormal matrix Q and the upper triangular matrix R such that A = QR.

We also show how to use this QR Factorization to calculate the eigenvalues/vectors of a symmetric square matrix. In fact, we can use the Eigenvalues/vectors option of the Matrix data analysis tool (or the functions eigVALSym and eigVECTSym) to calculate the eigenvalues/vectors.

It turns out that the algorithm described can be used to calculate any real-valued eigenvalues even for non-symmetric matrices, but while the eigenvector for the dominant eigenvalue is correct, the other eigenvectors generated aren’t necessarily correct for non-symmetric matrices. One way to find the correct eigenvectors is to use Schur’s factorization.

Basic Concepts

Definition 1: A Schur’s factorization (or Schur’s decomposition) of a square matrix A consists of an orthogonal matrix Q and an upper triangular matrix T such that A = QTQ^T.

Observation: Since by Property 6a of Orthogonal Vectors and Matrices, for an orthogonal matrix Q^-1 = Q^T, it follows from Property 9 of Eigenvalues and Eigenvectors that A and T have the same eigenvalues. But by Property 1d of Eigenvalues and Eigenvectors, the eigenvalues of T are the elements on the main diagonal. Thus, the eigenvalues of A are the elements on the main diagonal of T as well.

Also, since Q^-1 = Q^T, we know that A = QTQ^T is equivalent to T = A^TTA.

Property 1 (Schur’s Factorization): For any n × n invertible matrix A, we can construct a Schur’s factorization.

Proof: The proof is by induction on n. If n = 1, then if A = [a] then A = QTQ^T where Q = [1] and T = [a]. We now assume that the property holds for n and show how to construct a Schur’s factorization for the n+1 × n+1 matrix A.

Let λ be any real eigenvalue of A with corresponding real eigenvector X. These can be found using the QR factorization procedure of Definition 3 of QR Factorization. As usual, we can assume that ||X|| = 1. By Theorem 1 of Orthogonal Vectors and Matrices (Gram-Schmidt), we can construct an n+1 × n+1 orthogonal matrix P whose first column is X. Alternatively, we can construct P using QR Factorization as follows.

In fact, let B = [X E₁ E₂ … E_n] where E_i is a column vector all of whose elements are 0 except for the element in the ith row which is 1 (although if x_n+1 = 0, where x_n+1 is the n+1^th element in X, then replace E_i in the definition of B by E_n+1 for any i such that x_i ≠ 0; such an element exists since X ≠ O). Using Property 6 (QR Factorization), we can construct an orthogonal matrix P and upper triangular matrix R such that B = PR, where the first column of P  is X, and so P = [X C] for some n+1 × n matrix C.

Now since X^TAX = X^TλX = λX^TX = λ and C^TAX = C^TλX = λC^TX = λO = O, we have

where

By the induction hypothesis, there is an orthogonal matrix and upper triangular matrix  such that

Thus

Now define

Then T is upper triangular and Q is orthogonal. Furthermore

Observation: Note that the factorization is not unique. In particular, changing the order of the diagonal elements changes the factorization.

Example

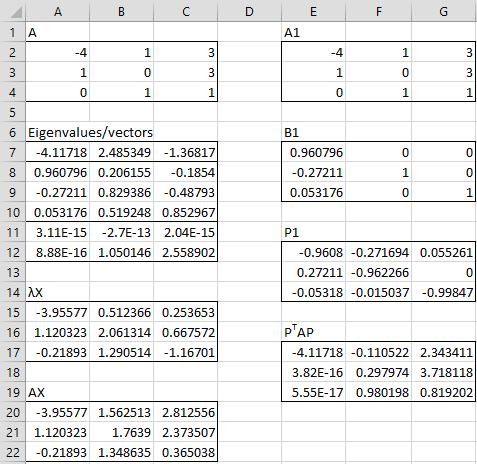
Example 1: Find the Schur’s Factorization for matrix A in range A2:C4 of Figure 1.

We highlight the range A7:C12 and enter the array formula =eVECTOR(A2:C4,500). The eigenvalues of A are found in range A7:C7, namely -4.11718, 2.485349, and -1.36817. Since range A11:C11 contains values of det(A−λI) close to zero, these values are true eigenvalues.

The unit eigenvector corresponding to the first eigenvalue is found in range A8:A10. Since the value in cell A12 is close to zero, this eigenvector is correct. This eigenvector is also entered in range E7:E9 to build the first B matrix (range E7:G9). Note that since the values in cells B12 and C12 are not close to zero, the vectors in B8:B10 and C8:C10 are not eigenvectors.

We now use the array formula =QRFactor(E7:G9) to calculate the P matrix (range E12:G14). Next we use the array formula

=MMULT(TRANSPOSE(E12:G14),MMULT(E2:G4,E12:G14))

to calculate P^TAP (range E17:G19).

Figure 1 – Schur’s Factorization (step 1)

We now repeat the above procedure on the 2 × 2 matrix A₂ which is formed from the lower right portion (i.e. range F18:G19) of P^TAP, which is repeated in range I2:J3 in Figure 2.

We use the formula =eVECTORS(I2:J3) to obtain the eigenvalues in range I6:J6 and potential eigenvectors in I7:I8 and J7:J8. Once again the first eigenvector is valid (cell I10 is near zero) and the second is not a valid eigenvector (cell J10 is not near zero). The 2 × 2 version of matrix B is shown in range L6:M7 and the corresponding matrix P is shown in range L10:M11 using the formula =QRFactor(L6:M7).

Figure 2 – Schur’s Factorization (step 2)

For any 2 × 2 matrix A, the P matrix is the Q matrix in Schur’s factorization of A. Thus the matrix in range L10:M11 is the Q matrix in Schur’s factorization of the matrix in range L2:M3. To calculate the corresponding T matrix, we first need to calculate P^TAP (range L14:M15) via the array formula

=MMULT(TRANSPOSE(L10:M11),MMULT(L2:M3,L10:M11)).

The four cells in T (range L18:M19) are calculated as follows: =I6 in cell L18, 0 in cell L19, =M14 in cell M18, and =J6 in cell M19.

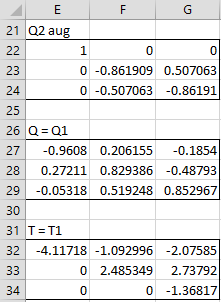
We now need to calculate the Q and T matrices for the original 3 × 3 matrix A in range A2:C4 of Figure 1. This is shown in Figure 3.

Figure 3 – Schur’s factorization (step 3)

We augment the Q₂ matrix (range L10:M11) from Schur’s factorization of A₂ as shown in range E22:G24, by placing zeros in the first row and column except for a 1 in the first cell and then Q₂ in the lower right portion of the matrix. The Q matrix in Schur’s factorization of our original matrix A is then calculated using the array formula =MMULT(E12:G14,E22:G24), as shown in range E27:G29.

The T matrix in Schur’s factorization is shown in range E32:G34. Here cell E32 contains the formula =A7, cells E33 and E34 contain zeros, range F32:G32 contains the array formula =MMULT(F17:G17,L22:M23) and range F33:G34 contains the array formula =L26:M27. We can also calculate the value of T by the formula

=MMULT(TRANSPOSE(E27:G29),MMULT(E2:G4,E27:G29))

We see that T is an upper triangular matrix and

Q^TQ = MMULT(TRANSPOSE(E27:G29),E27:G29)

is an identity matrix, thus proving that Q is orthogonal. Finally, we see that we can calculate QTQ^T by

=MMULT(E27:G29,MMULT(E32:G34,TRANSPOSE(E27:G29))) 

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack contains the following array functions to calculate Schur’s factorization for matrix A in range R1:

SCHUR(R1, iter, order): returns matrices Q and T such that A = QTQ^T is Schur’s factorization of A. If R1 is an n × n range, the output is a 2n × n range with matrix Q over T.

SCHURQ(R1, iter, order): returns only matrix Q of Schur’s factorization of A

The algorithm used is iterative with iter iterations (default 100). The diagonal of T contains the eigenvalues of A. If order = TRUE or -1 (default) then the eigenvalues are arranged in descending order based on their absolute values. If order = FALSE or 0 then the eigenvalues are in descending order. Finally, if order = +1 then the eigenvalues are not sorted at all.

Data Analysis Tool

Real Statistics Data Analysis Tool: The Schur’s factorization can also be created by using the Schur’s Factorization option of the Matrix data analysis tool.