Definition: An (upper) Hessenberg matrix is a square matrix where all the entries below the first diagonal below the main diagonal are zeros. Similarly, a lower Hessenberg matrix is a square matrix where all the entries above the first diagonal above the main diagonal are zeros.
A square matrix A is similar to a Hessenberg matrix if there exists a Hessenberg matrix H as well as an orthogonal matrix Q such that A = QTHQ (this is called a Hessenberg decomposition or Hessenberg factorization of A). In this case, QQT = QTQ = I and so Q-1 = QT.
A tridiagonal matrix is a square matrix that is both upper and lower Hessenberg (i.e. non-zero entries can only occur on the main diagonal or the first diagonal above or below the main diagonal).
Property 1: All square matrices are similar to a Hessenberg matrix.
Property 2: All symmetric matrices are similar to a tridiagonal matrix.
Real Statistics Functions: The following functions are provided in the Real Statistics Resource Pack. Here R1 is an n × n square array and prec is a small non-negative number (default 0.000000000001) where any value ≤ prec is considered to be equivalent to zero).
HessH(R1, prec): returns a Hessenberg matrix that is similar to the square matrix in R1.
HessQ(R1, prec): returns a matrix Q for which if H = HessH(R1, prec) then A = QTHQ.
HESS(R1, prec): returns a 2n × n array for the n × n matrix in R1 such that the first n rows are H and the last n rows are Q where H = HessH(R1, prec) and Q = HessQ(R1, prec)
Observation: The eigenvalues of a square matrix are the same as those of a Hessenberg matrix that it is similar to. Since Hessenberg matrices are simpler than other square matrices, to find the eigenvalues of a matrix it is usually worthwhile to first find a similar Hessenberg matrix and then find the eigenvalues of that matrix. Also if A = QTHQ is a Hessenberg decomposition of A and V is an eigenvector of H that corresponds to the eigenvalue λ (of H), then QV is an eigenvector of A that corresponds to the eigenvalue λ (of A).
Property 1 is constructive; in particular, we can find a similar Hessenberg matrix by using Householder reflections in a manner similar to that described for constructing a QR decomposition.
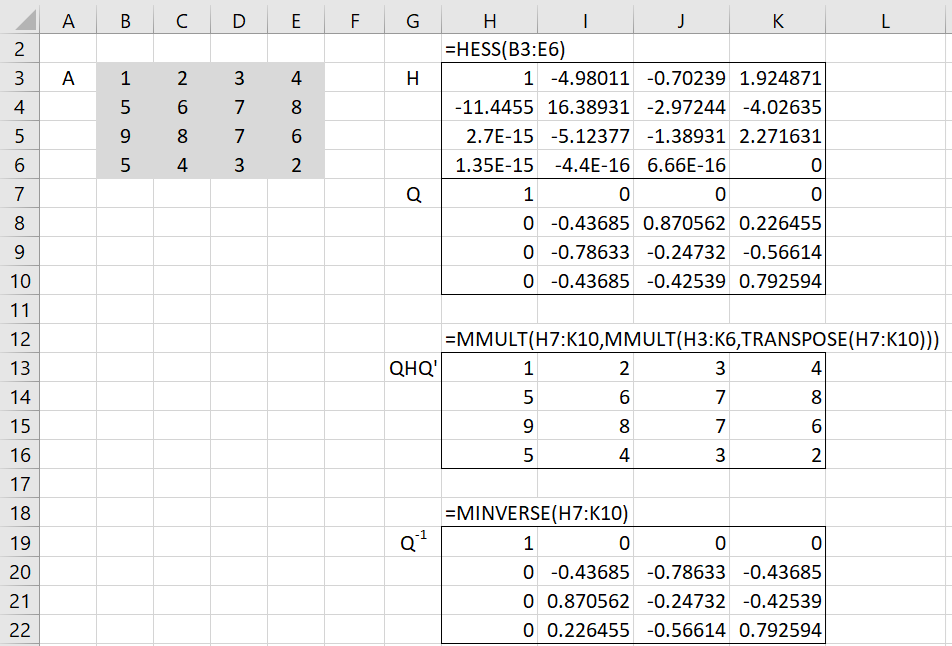
Example 1: Find the Hessenberg decomposition for the matrix in range B3:E6 of Figure 1.
Figure 1 – Hessenberg decomposition
We find the decomposition by placing the array formula =HESS(B3:E6) in range H3:K10. Note that A = QHQT, as can be seen in range H13:K16. We also see that H is an upper triangular matrix and Q-1 = QT.
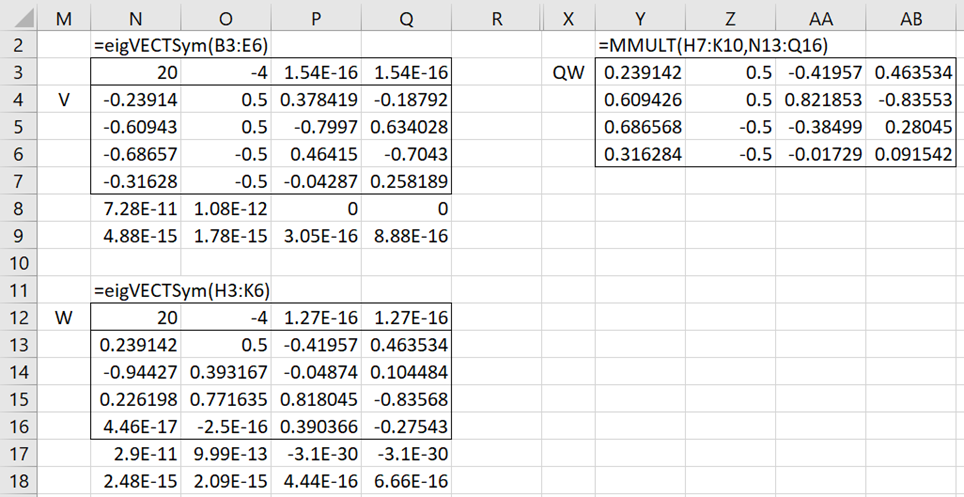
From Figure 2, we see that 20, -4, 0, 0 are the eigenvalues of matrix A, with corresponding eigenvectors V shown in the columns of range N4:Q7. We see that matrix H has the same eigenvalues as A, with eigenvectors W. The matrix product of QW shown on the right side of Figure 2 also yields 4 eigenvectors of A. The first two of these eigenvectors match those in range N4:Q7. While the last two eigenvectors don’t match exactly, they are alternative eigenvectors corresponding to the two zero eigenvalues.
Figure 2 – Eigenvectors
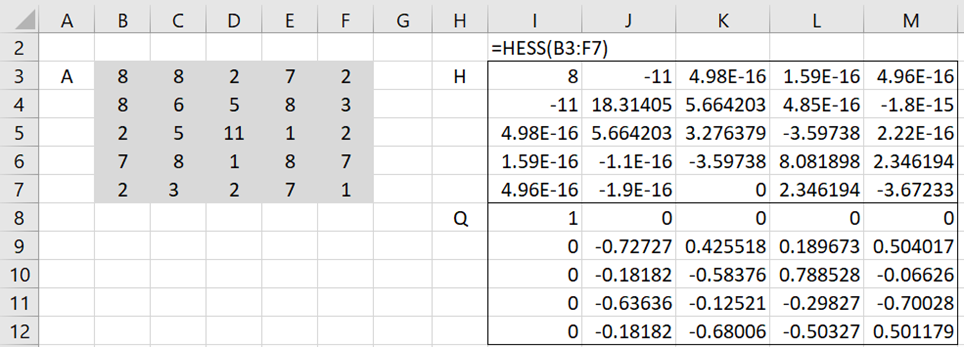
Example 2: Find the tridiagonal decomposition for the symmetric matrix in range B3:F7of Figure 2.
Figure 3 – Tridiagonal decomposition
Using the array =HESS(B3:F7), we calculate the H and Q matrices as shown in Figure 3. Note that this time H is a tridiagonal matrix.