4-level Interactions
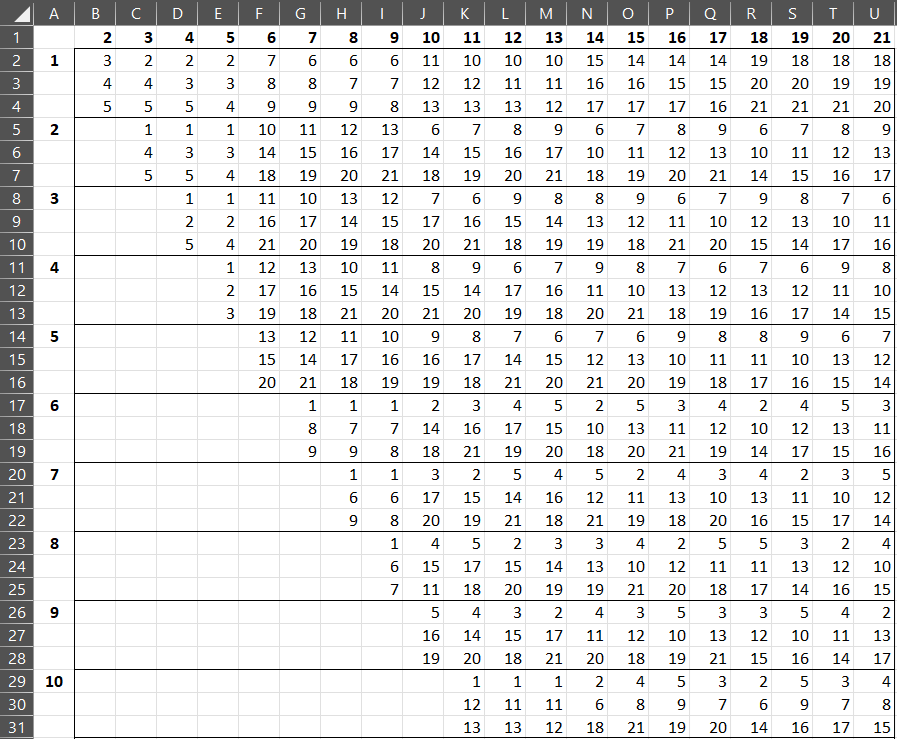
The L16 4 and L64 4 designs permit interaction factors as described in Figure 1. Note that the interactions take up three columns in the design.
Since any interaction requires three of columns 1, 2, 3, 4, and 5, this design can only support at most one interaction.
Figure 1 – Interactions for L16 4 and L64 4 designs
Example
For example, suppose that we need a design with 6 main effects factors and one interaction. We can’t use the L16 4 design since it only accepts 5 factors (including interactions). We therefore elect to use the L64 4 design and assign factors A and B to columns 1 and 2. Based on Figure 1, we need to use columns 3, 4, and 5 to the interaction AB.
We can also use the formula =TInteract(1,2,4) to obtain a row array containing the values 3, 4, and 5.
For example, we can use the design shown in Figure 2 (only the first 5 rows are displayed).
Figure 2 – Design with 4-level factors including an interaction
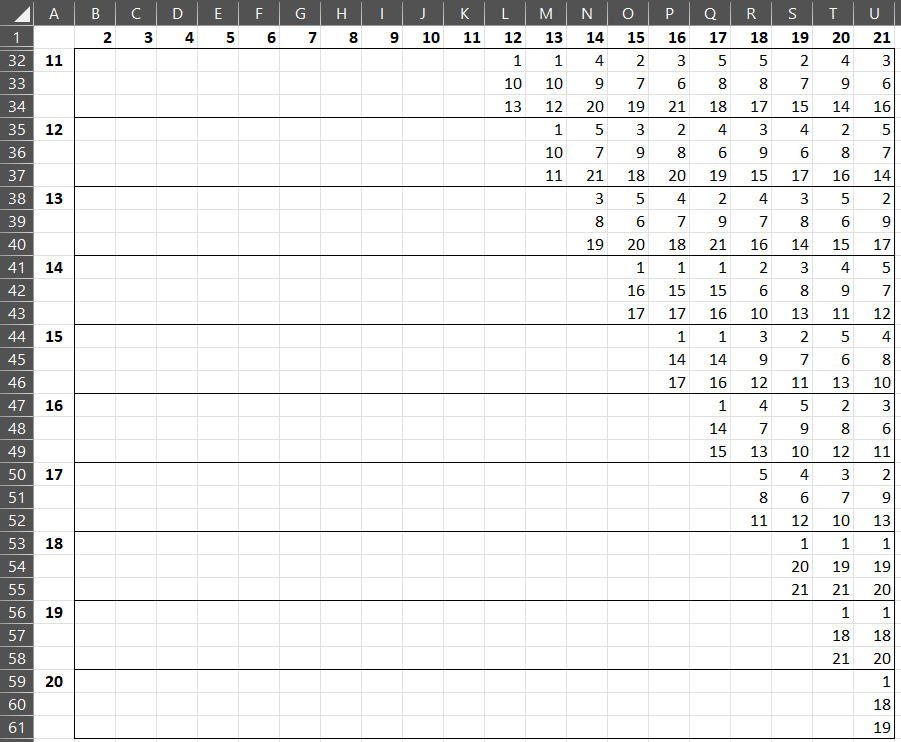
As described for Example 2 of 3-level Taguchi Design Examples, since all the factor labels need to be unique, we need to place the labels AB in columns 3, 4, and 5 but with some distinct third symbol appended to AB.
2-level Interactions
As mentioned in 4-Level Taguchi Designs, although L16 42a doesn’t support interactions of 4-level factors, it does support interactions of 2-level factors. The reason for this is that you can map each of the 2-level columns in the L16 42a design to a column in L16 2 design. This mapping is shown in range E19:J19 of Figure 3.
Figure 3 – 2-level interaction for L16 42a
If you extract just the interactions for columns 6, 7, 9, 11, 13, and 14 of the L16 2 design from the Interaction Table in Figure 4 of Taguchi 2-level Designs, you obtain the table shown in range AC5:AG9 of Figure 3. Using the inverse map this becomes the Interaction Table shown in range AC13:AG17 of Figure 3 for the L16 42a.
We get the same results if we use the TInteract function setting levels equal to 16.
Example
Thus, we can support two 4-level factors, three 2-level factors plus two interactions using the L16 42a design shown in Figure 4.
Figure 4 – L16 42a design (part 1)
Since =TInteract(4,7,16) returns the value 8 and =TInteract(5,6,16) returns the value 9, we are able to place the 2-level factors, C, D, E, F, CF, and DE, as shown on the left side of Figure 4.
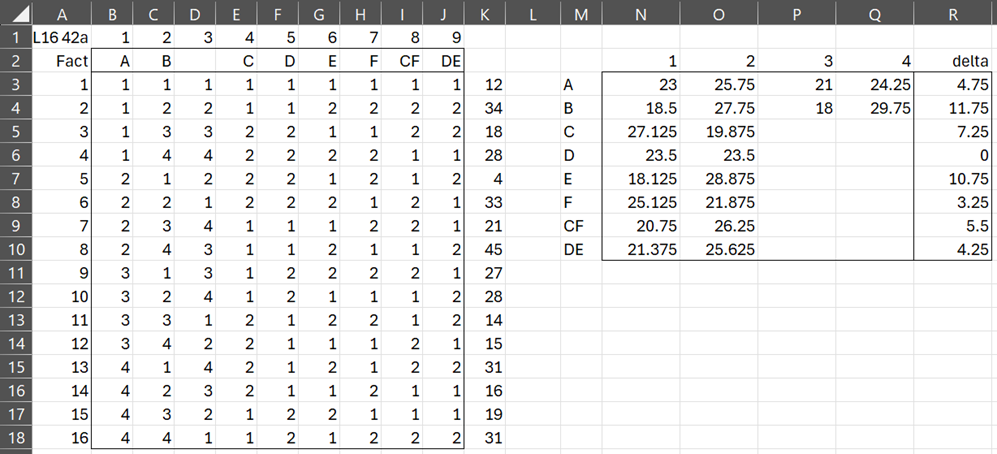
The output from the design using the Taguchi DOE data analysis tool (see Real Statistics Support for Taguchi DOE) continues as shown in Figure 5.
Figure 5 – L16 42a design (part 2)
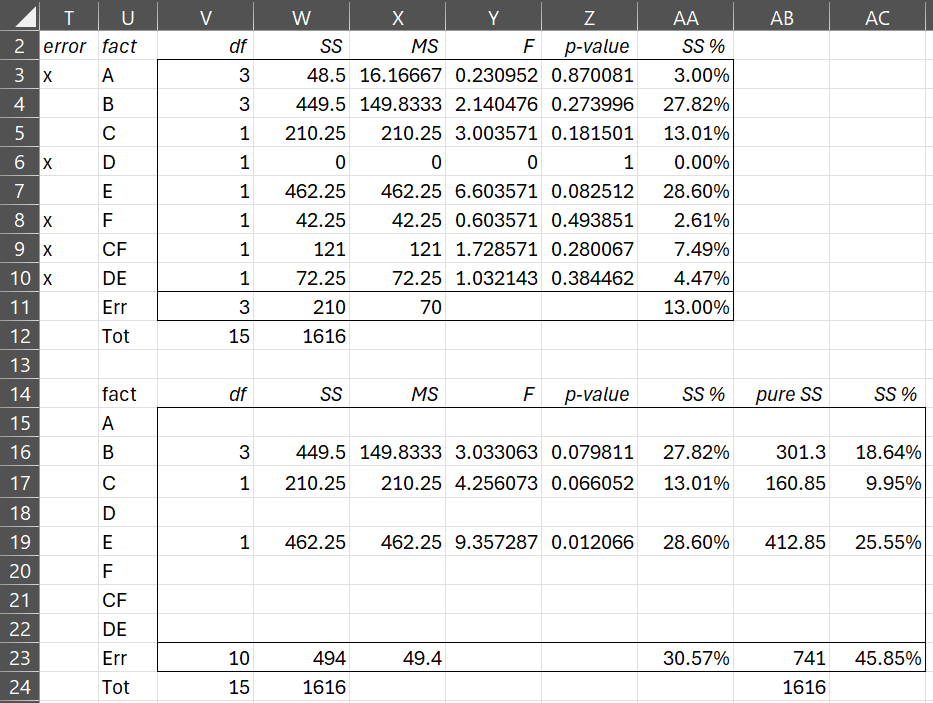
Note that there are 42 × 24 = 256 combinations of the main effects factors and levels. Since this number is larger than 240, the Taguchi DOE data analysis tool returns the optimum combination only and not a list of all 256 combinations, as shown in Figure 6 (based on “bigger is better”).
Figure 6 – L16 42a design (part 3)
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Roy, R. K. (2010) A primer on Taguchi method. 2nd ed. Society of Manufacturing Engineers
https://brharnetc.edu.in/br/wp-content/uploads/2018/11/11.pdf
University of York (2004) Orthogonal arrays (Taguchi designs)
https://www.york.ac.uk/depts/maths/tables/orthogonal.htm
Minitab (2024) Catalogue of Taguchi designs
https://support.minitab.com/en-us/minitab/help-and-how-to/statistical-modeling/doe/supporting-topics/taguchi-designs/catalogue-of-taguchi-designs/