RCBD Follow-up Testing

As we can see from cell O13 of Figure 5 of Randomized Complete Block Design, there is a significant difference in crop yield between the various dosages of herbicide for Example 1 of Randomized Complete Block Design. We can now perform a number of follow-up tests as described in Planned Follow-up Tests and Unplanned Follow-up Tests. In particular, the Real Statistics Resource Pack supports Contrasts and Tukey’s HSD.

Example 1: Use Contrasts to determine whether there is a significant difference in yield between 10 units of herbicide and (the average of) the other dosages for Example 1 of Randomized Complete Block Design.

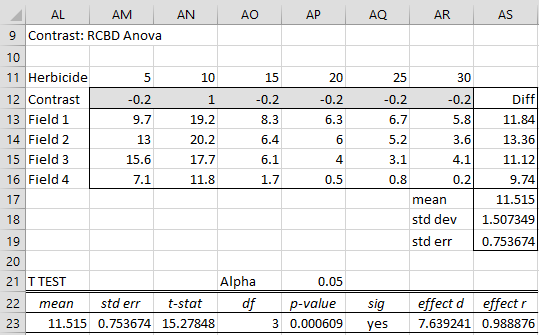
We can use the RCBD data analysis tool, as described in Randomized Complete Block Design, this time checking the Contrasts option of Figure 4 of Randomized Complete Block Design. Since we only need to perform one contrast we retain the default number of contrasts of 1 in the Alpha correction for contrasts. The output is shown in Figure 1, where initially range AM12:AR12 is empty.

Figure 1 – Contrasts for RCBD

We now fill in range AM12:AR12 with the contrast coefficient values shown in Figure 1. We see from cell AQ23 that there is a significant difference between the yield using a 10 unit dosage and the average of the other dosages.

If we had wanted to perform multiple contrasts in order to control familywise error, we would choose the Bonferroni or Dunn/Sidak option in the Alpha correction for contrasts portion of the dialog box and change the number of contrasts from the default of 1 to the number of contrasts we planned to perform.

Observation: To get more information about how the various cells in Figure 1 are calculated, see Figure 4 of Repeated Measures Anova since the calculations are similar to those for contrasts for ANOVA with Repeated Measures.

Example 2: Use Tukey’s HSD to determine which dosages from Example 1 are significantly different.

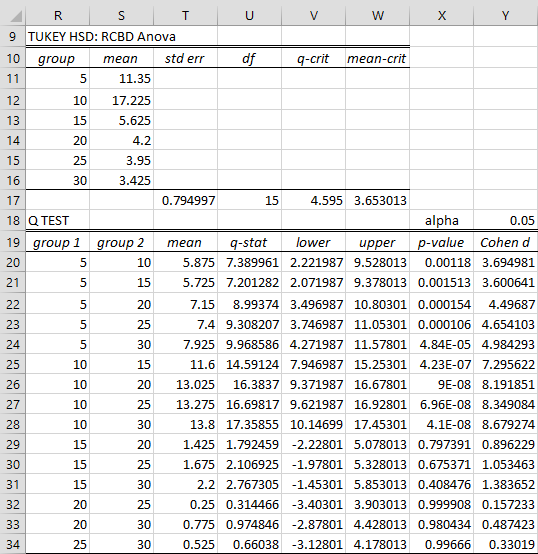
We can again use the RCBD data analysis tool, as described in Randomized Complete Block Design, this time checking the Tukey HSD option in Figure 4 of Randomized Complete Block Design. We start by filling in the contrast coefficients in range AB11:AB16 as shown in Figure 2.

Figure 2 – Tukey’s HSD for RCBD

We see that p-value = .00118 < .05 = α, which means that there is a significant difference in yield between 5 units and 10 units. Thus, we can conclude that there is a significant difference between 5 units and any of the other dosages. Similarly, we see there is a significant different difference between 10 units and 15 units, and therefore between 10 units and any of the other dosages. We can also see that there is not a significant difference between any of the pairs of dosages among 15, 20, 25 and 30 units.

See Figure 3 for how some representative cells in Figure 2 are calculated (with reference to cells in Figure 1 and 5 of Randomized Complete Block Design).

Cell	Entity	Formula
S11	mean for group 5	=AVERAGE(B4:B7)
T17	standard error	=SQRT(M15/COUNT(B4:B7))
U17	df	=L15
V17	q-crit	=QCRIT(COUNT(S11:S16),U17,Y18,2)
W17	mean-crit	=T17*V17
T20	mean diff groups 5 and 10	=ABS(S11-S12)
U20	q-stat	=T20/T$17
V20	lower conf interval	=T20-W$17
W20	upper conf interval	=T20+W$17
X20	p-value	=QDIST(U20,COUNT(S$11:S$16),U$17)
Y20	effect size d	=U20/SQRT(COUNT(B$4:B$7))

Figure 3 – Representative formulas from Figure 2

Example 3: Use the modified version of Tukey’s HSD to determine which dosages from Example 1 are significantly different. This means that instead of using the ANOVA MSE value to compute the standard errors (as in cell T17), we calculate the standard errors directly based on the data for each comparison.

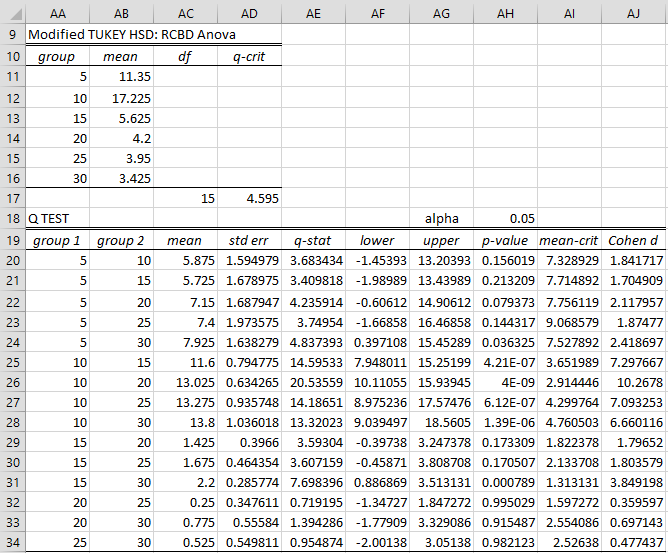
Once again, we use the RCBD data analysis tool, as described for Example, this time checking the Modified Tukey HSD option of Figure 4 of Randomized Complete Block Design. The result is shown in Figure 4.

Figure 4 – Modified Tukey’s HSD for RCBD

This time, we see that the only significant comparisons are between 10 units and any of the other dosages, as well as between 15 and 30 units.

The formulas used are similar to those in Figure 3, with the principal difference the formula used to calculate the standard errors. E.g. the array formula in cell AD20 is =STDERR(MSUB(B4:B7,C4:C7)). Here the MSUB function is used to subtract the elements in column B from the corresponding element in column C, ignoring any pair where one or both of the elements are non.numeric. This is important when there are missing data elements (as described in RCBD with One Missing Data Element and RCBD using Regression). Also, the dfE value in cell AC17 is calculated using the formula =dfWF(B12:G15,1).