Simpson’s Diversity Index

Basic Concepts

Another measure of diversity is based on the probability that any two elements selected at random will belong to the same category, i.e.

Simpson's diversity index

where ni is the number of observations from the sample in the ith of k (non-empty) categories, n is the sample size, and pi = ni/n.

Since diversity corresponds to a low value of D and lack of diversity corresponds to a high value, it is better to use 1 – D, which is called Simpson’s index of diversity. This index takes values between 0 and 1.

Another measure is Simpson’s reciprocal index of diversity, which is defined as 1/D. This index takes values between 1 and k.

The above approach assumes sampling with replacement. For small samples, it is better to use sampling without replacement, in which case D is defined as

image138c

Note that it is common to study the measure 1 – D′ or 1/D′.

Example

Example 1: Repeat Example 1 of Shannon’s Diversity Index using Simpson’s index of diversity.

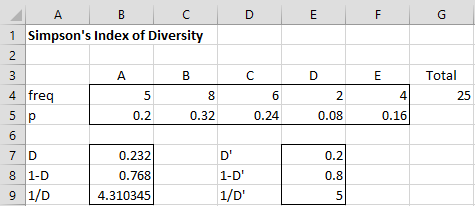
Simpson's diversity index

Figure 1 – Simpson’s Diversity Index

Figure 1 shows the D and 1/D indices. Cell B7 contains the formula =SUMSQ(B5:F5) and cell E7 contains the formula =SUMPRODUCT(B4:F4,B4:F4-1)/(G4*(G4-1)).

Note that for a large population, the maximum value of D is 1/k, and so the maximum value of 1/D is k. Thus we can use  (1/D)/k  = 1/Dk  as an index of homogeneity.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Offwell Woodland & Wildlife Trust (2016) Simpson’s diversity index. Ecological sampling methods
http://www.countrysideinfo.co.uk/simpsons.htm

Wikipedia (2016) Diversity index
https://en.wikipedia.org/wiki/Diversity_index

8 thoughts on “Simpson’s Diversity Index”

  1. Hi Charles,

    Thanks for the free package and this website which is really helpful for learning how to do diversity indices on excel!

    I have followed the instructions on this webpage and have results for the diversity indices. However, I noticed that on the example above, there is a row that has p (on the example it is cell A5). I was wondering what this was, and if I were to utilize this, how would I do this on excel with the package?

    I have one more question. The output for the Simpson’s diversity index also has another column titled “Sm Sample”. I was wondering what the data in this column was?

    Thanks,
    S. A.

    Reply

    • Sabre,
      Row 5 contains the probabilities corresponding to the frequencies in row 4. E.g. cell B5 contains the formula =B4/$G4.
      Sm Sample stands for the small sample version of Simpson’s index. This is described on the Simpson’s Index webpage.
      Charles

      Reply

  2. How would you best proceed when you need the Simpson Index applied to hundreds of various locations in order to compare variability between location? Is excel capable of processing that or is a stat software the only possibility? Thanks

    Reply

  4. emm type 2 N(No) N(Yes)
    28 90 57
    89 80 61
    1 77 60
    4 41 34
    12 36 28
    3 20 20
    6 17 20
    77 21 14
    44 11 23
    83 13 7
    75 20 27
    66 1 13
    87 9 17
    2 9 5
    11 3 5
    81 7 1
    86 1 5
    63 3 2
    108 0 5
    82 3 2
    9 2 2
    22 2 2
    88 4 0
    92 2 2
    102 2 2
    5 1 2
    53 0 3
    58 1 2
    76 1 2
    95 1 2
    100 0 3
    118 1 2
    169 1 2
    8 2 0
    49 0 2
    73 1 2
    80 1 1
    94 1 1
    110 0 2
    103 0 2
    13 0 1
    25 1 0
    29 0 1
    32 0 1
    42 1 0
    48 0 1
    54 0 1
    60 0 1
    65 1 0
    68 0 1
    85 1 0
    72 1 0
    90 0 1
    104 0 1
    105 0 1
    112 0 1
    116 0 1
    121 1 0
    180 0 1
    230 0 1
    183 0 1

    Reply

Leave a Comment