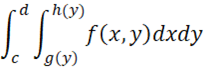Real Statistics Release 8.3

The following is an overview of the new features in Release 8.3.

Moderation Analysis

This release adds a new data analysis tool that performs Moderation Analysis. This tool is now included as an option on the Reg tab of the main menu.

See Moderation Analysis for more information.

Total Least Squares Regression

This release adds a new worksheet array function TRegPARAM that returns the coefficient, standard error, and lower/upper ends of the 1-α confidence interval for the intercept and slope coefficients based on total linear regression.

See TLS Regression Confidence Interval for more information.

Jackknife Support

The Real Statistics Resource Pack currently supports jackknifing to estimate the standard error and confidence intervals for Deming regression and the Gini Index. This release adds general jackknife support for any parameter using the Real Statistics lambda capability. The new function takes the form

JACKKNIFE(R1, expression, ref): returns a column array with the jackknife sample for the data in R1 based on the function f(arr) on a variable arr that takes array values; expression is used to specify f and ref is an optional reference to arr.

If R1 is a column array with elements S = {x₁, …, x_n}, then jackknifing works by creating n data sets S₁, …, S_n where S_j is equal to S with x_j removed. The jackknife sample is then a column array containing the elements f(S₁), …, f(S_n).

If R1 is an array with multiple columns then the same approach is used except that now the x_i represent rows in R1.

Bootstrapping

The Real Statistics Resource Pack currently supports bootstrapping in a number of contexts. In particular, it is used  in the Resampling Data Analysis tool, but it is also used to estimate the standard error and confidence intervals for order statistics and various distribution parameters.

In a fashion similar to that described above for jackknifing, in this release, we add more general support via the following function, which uses Real Statistics’ lambda capability.

BOOTSTRAP(R1, expression, iter, ref): returns a column array with a bootstrap sample for the data in R1 based on the function f(arr) on a variable arr that takes array values; expression is used to specify f and ref is an optional reference to arr.

R1, expression, and ref are as for JACKKNIFE. iter is the number of bootstrap samples returned (default 2,000).

If R1 is a column array with elements S = {x₁, …, x_n}, then bootstrapping works by creating iter data sets S₁, …, S_iter where each S_j is formed by taking n elements from S with replacement. The bootstrap sample is then a column array containing the elements f(S₁), …, f(S_iter).

If R1 is an array with multiple columns then the same approach is used except that now the x_i represent rows in R1.

Confidence Intervals using Bootstrapping

Typically, bootstrapping is used to estimate the confidence interval of a parameter using the values of a finite sample. The following worksheet function has been added to provide this estimate.

CI_BOOTSTRAP(R1, expression, lab, iter, alpha, ref): returns various statistics resulting from a bootstrap sample for the data in R1 based on the function f(arr) on a variable arr that takes array values; expression is used to specify f and ref is an optional reference to arr.

R1, expression, ref, and iter are as for BOOTSTRAP. alpha takes a value between 0 and .5 (default .05).

The statistics that are returned are:

• parameter estimate = f(arr) where arr is the R1 array
• bootstrap estimate = the average of the f(S₁), …, f(S_iter) for bootstraps S_j
• standard error = the standard deviation of the f(S₁), …, f(S_iter)
• percentile confidence interval (% lower, % upper) where % lower = the alpha*iter smallest value of f(S_j) and % upper = the alpha*iter largest value of f(S_j)
• BC_a (bias-corrected and accelerated) confidence interval (BC_a lower, BC_a upper) = the BC_a adjusted value of the percentile confidence interval

If lab = FALSE (default), then the output consists of a column array with the above 7 entries. If lab = TRUE, then an extra column is appended to the output consisting of labels.

The BC_a confidence interval uses an acceleration adjustment. This is calculated from the jackknife of the data in R1 using the following new worksheet function.

Acceleration(R1, expression, ref) = the acceleration for the sample data in R1 based on the function f(arr) on a variable arr that takes array values; expression is used to specify f and ref is an optional reference to arr.

Generalized Pareto Distribution

The following new worksheet functions have been added for the Generalized Pareto distribution (GPD).

GPD_DIST(x, μ, σ, ξ, cum) = the pdf of the GPD when cum = FALSE and the corresponding cumulative distribution function when cum = TRUE.

GPD_INV(p, μ, σ, ξ) = the inverse of the GPD at p

Here, μ is the location parameter, σ is the scale parameter and ξ is the shape parameter.

The following data fitting function has also been added.

GPD_FITM(R1, mu, lab, pure): returns a column array with the σ, ξ, and LL GPD parameters that fit the data in the column array R1, using location parameter mu, based on the method of moments. lab and pure are as described in Method of Moments: Real Statistics Support.

The One-sample Anderson-Darling test has been updated to determine whether  sample data fits a Generalized Pareto distribution using estimates of the three distribution parameters based on sample data.

The table of critical values for the Anderson-Darling test has been updated for the GPD for samples of size between 10 and 100.

The following functions, described in One-Sample Anderson-Darling Test, have been modified to support the GPD where dist takes the value 11, “pareto”, or “gpd”.

ANDERSON(R1, dist)

ADTEST(R1, dist, lab, iter, alpha)

ADCRIT(n, alpha, dist,, interp)

ADPROB(x, dist, n, iter, interp, txt)

The sample size value n must be supplied for ADCRIT and ADPROB.

Note that the GPD is not yet supported on the Goodness of Fit data analysis tool.

Double Integration

This release adds a new worksheet function INTEGRAL2 that provides a numerical estimate for double integrals of the following form

Here, g(y) and h(y) are functions of y, including constant functions. d is a constant or ∞ and c is a constant or -∞.

See Numerical Double Integration for more information.

New Sampling Functions

The existing Real Statistics RANDOMIZES(R1) and SHUFFLES(R1) array functions can be used to create a random sample (with and without replacement) from the data in R1.

In this release, we add the RANDOMIZERows(R1) and SHUFFLERows(R1) array functions that create a random sample (with and without replacement) based on the rows in R1.

See Sampling using Real Statistics Capabilities for more information.

New Wordle Support

The BestGuess2(guess1, pattern1, ttype) function has been revised.

This function now returns a row array with the following elements (the last two are new):

1. the second guess with the highest number of non-zero patterns, but if there is more than one of these, then the guess whose largest number of targets for any pattern is the lowest
2. the number of non-zero patterns for this guess
3. the number of other guesses with the same number of non-zero patterns
4. the largest number of possible targets for this guess for any pattern.

The following new worksheet functions have been added.

Pattern2Counts(guess1, pattern1, guess): returns a column array with 243 rows, one for each pattern, with the count of targets that are compatible with guess1/pattern1 for the first guess and compatible with guess/pattern for the second guess. 

WordleProb2(guess1, pattern1, guess, lab); returns a column array containing the following entries where guess1/pattern1 represents the first guess and guess represents the second guess: # of non-zero patterns, # of compatible targets, probability of winning within 2, 3, 4, 5, and 6 tries, worst case pattern, and # of targets for that pattern. If lab = TRUE then a column is appended to the output with labels (default is FALSE).

Guesses2(guess1, pattern1, npatterns, ttype); returns a column array containing all the words in the dictionary that are compatible with guess1/pattern1 and have npatterns many non-zero patterns. ttype is as for BestGuess2.

In the above, guess1 and guess are text strings representing 5 letter English words, and pattern1 and pattern are positive integer values between 1 and 243 representing a pattern (e.g. 1 represents “*****”).

Other Enhancements

• The MPROD function, which returns the product of 3 or 4 matrices, can now also return the product of two matrices (and so is equivalent to MMULT in this case)
• The Array2String function, which converts an array to a text string using comma and semi-colon delimiters, now supports row arrays.
• A new SMALLExact(R1, k) function has been added. When k is an integer, then this function is equivalent to SMALL(R1,k). Otherwise, it takes the interpolated value =SMALL(R1,INT(k))+(k-INT(k))*(SMALL(R1,INT(k)+1)-SMALL(R1,INT(k))).
• A new FISHER_MIDP(R1, tails) function has been added that returns the mid-p correction for Fisher’s exact test. Here R1 is a 2 × 2 array and tails = 1 or 2 (default). This is a less conservative version of Fisher’s exact test for 2 × 2 contingency tables. See Fisher Exact Test for more information.
• A new XSTANDARDIZE(R1) array function has been added that is equivalent to the array formula =STANDARDIZE(R1,AVERAGE(R1),STDEV.S(R1)).
• A new COX_STUART(R1) array function with the p-value of the Cox-Stuart trend test and the direction of the trend. See Cox-Stuart Test for more information.