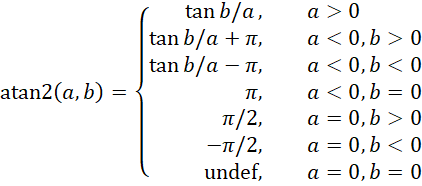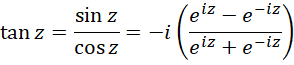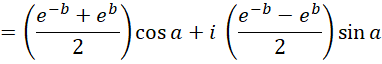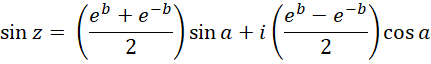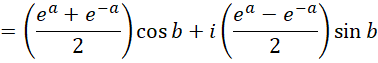Advanced Complex Number Operations

Euler’s Formula

Property A (Euler’s Formula): For any complex number z = a + bi

Proof: For any real number z

The same formula holds for a complex number z (in fact, this can be viewed as the definition of e^z). So, if z = bi, where b is a real number, then

But

i⁰ = 1, i¹ = i, i² = -1, i³ = –i, i⁴ =1, i⁵ = i, etc.

Thus

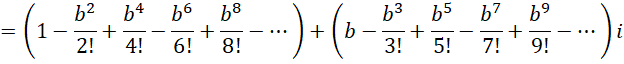
where we use the infinite sum representations of sin b and cos b for real numbers b.

If z = a + bi, then

Property B (Euler’s identity)

Proof: By Property A

= 1 ⋅ (-1 + i ⋅ 0) = -1

Actually

Log Function

If z is a complex number, by definition, if ln z = w, then z = e^w. Suppose that z = a + bi. As described in Complex Numbers in Polar Format, we can represent z in polar format as

where

Here

Thus

This proves the following property.

Property C

This formula is well defined except for z = 0 since r > 0 otherwise. Note that actually there are infinitely many results, as described below, since

Note that the principal value of the natural log is the one where -π < θ ≤ π, i.e. where n = 0.

Examples

Find ln(-1), ln(i) and ln(-i).

The polar form for -1 is r = 1 and θ = π. Thus

ln(-1) = ln 1 + i(π) = iπ

The polar form for i is r = 1 and θ = π/2. Thus

ln(i) = ln 1 + i(π/2) = iπ/2

The polar form for –i is r = 1 and θ = –π/2. Thus

ln(i) = ln 1 + i(-π/2) = –iπ/2

Power of a real number

Property D: For any complex number z = a + bi and any real number c > 0

c^z = c^a(cos(b ln c) + sin(b ln c))

Proof: Using Property A and the fact that z ln c = a ln c + (b + ln c)i

c^z = (e^{ln c})^z = e^{z ln c} = e^{a ln c}(cos(b ln c) + sin(b ln c))

= (e ^{ln c})^a ⋅ (cos(b ln c) + sin(b ln c))

=c^a(cos(b ln c) + sin(b ln c))

It turns out that this property holds even when c < 0. In this case, however, ln c is a complex number.

Multiple Representations

Since

cos(b+2πn) = cos(b)          sin(b+2πn) = sin(b)

for any integer n, from Property A it follows that

e^z = e^a(cos(b+2πn) + sin(b+2πn))

If e^z = w, then w = ln z. Thus, the natural log has infinitely many representations. If z = a + bi is one of these, then so are z = a + (b+2πn)i for any n.

Power function

We now show how to calculate z^w for any complex numbers z = a + bi and w = c + di.

As described above, we can express z in polar format as z = re^θi. Then using Property C

z^w = (e ^{ln z})^w = e^{w ln z} = e^{w (ln r + θi)} = e^{w ln r} ⋅ e^wθi = r^we^wθi

= r^c+di e^(c+di)θi = r^c r^di e^-dθ+cθi = r^c e^{lnr⋅ di} e^-dθ e^cθi = r^ce^-dθ ⋅ e^{(d⋅lnr+cθ)i}

Now by Property A

z^w = r^ce^-dθ ⋅ e^{(d⋅lnr+cθ)i} = r^ce^-dθ (cos φ + i sin φ)

where

φ = d lnr + cθ

Note that all the calculations involve only real numbers.

Also, when w is a real number, i.e. d = 0, then

z^w = r^c ⋅ e^cθi = r^c(cos cθ + i sin cθ)

Examples

Find 2ⁱ, (-2)ⁱ, √i, iⁱ, i^1/i, i^√2

2ⁱ – The polar form for 2 is r = 2 and θ = 0. Thus φ = 1 ln2 + 0 = ln2 ≈ .693147

2ⁱ = 2⁰e^–0 (cos ln2 + i sin ln2) ≈ cos .693147 + i sin .693147 ≈ .769239 + .638961i

(-2)ⁱ – The polar form for -2 is r = 2 and θ = π. Thus φ = 1 ln2 + 0 = ln2 ≈ .693147

(-2)ⁱ = 2⁰e^–1⋅π (cos ln2 + i sin ln2) ≈ e^-π (cos .693147 + i sin .693147)

≈ .043214(.769239 + .638961i) = .033242 + .027612i

√i = i^1/2 – The polar form for i is r = 1 and θ = π/2. Thus φ = 0 + (π/2)(1/2) = π/4

√i = 2⁰e^–0 (cos π/4 + i sin π/4) = √2/2 + i √2/2  ≈ .707107 + .707107i

iⁱ – The polar form for i is r = 1 and θ = π/2. Thus φ = 0 + 0 = 0

iⁱ = 2⁰e^–π/2 (cos 0 + i sin 0) = e^–π/2(1 + 0i) = e^–π/2  ≈  .20788

i^1/i = i^(1/i)(i/i) = i^{i/i^2} = i^i(-1) = i^-i = 1/iⁱ = 1/e^–π/2 = e^π/2 ≈  4.810477

i^√2 – The polar form for i is r = 1 and θ = π/2. Thus φ = 0 + (π/2)√2 ≈ 2.221441

i^√2 ≈ 2⁰e^–0 (cos 2.221441 + i sin 2.221441) ≈ -.6057 + .795693i

Multiple Representations

Since the power function uses the log function, there are multiple values. In particular

z^w = r^ce^{-d(θ + 2πn)} (cos φ + i sin φ)

where

φ = d lnr + c(θ + 2πn)

nth Root

z^1/n = (re^iθ)^1/n = r^1/n e^iθ/n

As we saw in Complex Numbers in Polar Format, there are actually n solutions

z^1/n = r^1/n e^i(θ+2πk)/n

for k = 0, 1, …, n-1.

For rational exponents m/n where lcd(m,n) = 1

z^m/n = r^m/n e^{i(θ+2πk)m/n}

Thus, once again there are n solutions. For all other cases of z^w there are infinitely many solutions.

Square Root

As we have seen previously, for any real number c

z^c = r^c ⋅ e^cθi = r^c(cos cθ + i sin cθ)

In particular,

z^1/2 = √r (cos θ/2 + i sin θ/2)

As we have noted previously, there are two solutions. Just as for real z, the other solution is the negative of the one given above.

Trig Functions

We define the trigonometric functions for complex numbers so that Euler’s formula holds, namely

e^zi = cos z + i sin z

Thus

e^zi + e^–zi = (cos z + i sin z) + (cos (-z) + i sin (-z))

= (cos z + i sin z) + (cos z – i sin z) = 2 cos z

which means that

Similarly

Thus

In addition

Similarly

Inverse trig functions

Finally, note that

If w = arctan z then also w + nπ = arctan z, i.e. tan(w+nπ) = z

arctan(z) is not defined for z = nπ/2 for any odd integer n

If w = arccos z then also w + 2πn = arccos z

If w = arcsin z then also w + 2πn = arcsin z

It also turns out that if w = arcsin z then also π – w = arcsin z

Hyperbolic trig functions

Now if z = a + bi

Similarly

Worksheet Functions

Real Statistics Functions: Starting with Rel 9.8, the Real Statistics Resource Pack will provide the following functions for any complex numbers z and w. Some of these functions are already provided prioer to Rel 9.8, but with fewer arguments.

CPOWER(z, w, n, prec) = zw	CSQRT(z) = √z
CSIN(z, prec) = sin(z)	CASIN(z, n, prec, neg) = arcsin(z)	CSINH(z, prec) = sinh(z)
CCOS(z, prec) = cos(z)	CACOS(z, n, prec) = arccos(z)	CCOSH(z, prec) = cosh(z)
CTAN(z, prec) = tan(z)	CATAN(z, n, prec) = arctan(z)	CTANH(z, prec) = tanh(z)
CLN(z, n, prec) = ln z	CEXP(z, prec) = ez	CI() = i
CMULT(z, w, prec) = z * w	CDIV(z, w, prec) = z/w

n takes an integer value and is used for multivalued functions as described above. n defaults to zero.

If the output that the form a + bi, then if a < prec then a is reset to 0. Similarly, if b < prec then b is reset to 0. prec defaults to 0.0000000000001.

Note that CSIN(CASIN(z, n)) = z for any z and n, but CASIN(SIN(z, n) is not necessarily equal to z. This is true for the cosine and tangent functions as well.

Finally, as described previously, if w = arcsin(z) then also π – w = arcsin(z). When neg = TRUE (default FALSE), then this form of arcsin is used. Thus, =CASIN(z, n, , TRUE) takes the same value as =CSUB(Pi(),CASIN(z,n)) and CSIN(CASIN(z, n, , neg)) = z for either value of neg.

Links

↑ Other mathematical topics

References

Redcrab (2026) Complex numbers online calculator
https://www.redcrab-software.com/en/Calculator/Complex

Proof Wiki (2026) Definition: inverse tangent/complex
https://proofwiki.org/wiki/Definition:Inverse_Tangent/Complex

Prabhat, A. (2021) Top 10 trigonometric functions for complex numbers in Excel
https://quickexcel.com/trigonometric-functions-complex-numbers/